Вопросы для допуска к выполнению лабораторной работы

1. Что такое колебательный контур?

2. Нарисуйте схему последовательного колебательного контура.

3. Объясните механизм возникновения электромагнитных колебаний в колебательном контуре.

4. В каком случае свободные колебания, возникающие в колебательном контуре, являются гармоническими незатухающими? Затухающими? Нарисуйте соответствующие графики.

5. В каких случаях к колебательному контуру можно применять закон сохранения энергии, а в каких – нет?

6. Как зависит от времени амплитуда затухающих колебаний? Нарисуйте график.

7. Что такое фазовая кривая? Нарисуйте фазовые кривые для гармонических и для затухающих колебаний.

8. Дайте определение коэффициента затухания; логарифмического декремента затухания. Как на них влияет величина сопротивления контура?

Контрольные вопросы

1. Нарисуйте схему колебательного контура. Запишите для него второе правило Кирхгофа.

2. Получите дифференциальное уравнение затухающих колебаний и запишите его решение. Запишите выражение для частоты затухающих колебаний. Как она зависит от сопротивления контура?

3. Нарисуйте график затухающих колебаний. По какому закону уменьшается амплитуда затухающих колебаний?

4. Дайте определение коэффициента затухания, собственной частоты колебаний контура, декремента и логарифмического декремента затухания.

5. Как в данной работе экспериментально определяется логарифмический декремент затухания? Докажите формулу (13.15).

6. Дайте определение добротности. В чем заключается ее физический смысл? Как она зависит от сопротивления контура?

7. При каких условиях в колебательном контуре возникает апериодический процесс?

8. Сформулируйте понятия фазовой плоскости и фазовой кривой. Нарисуйте фазовые кривые для затухающего колебательного и апериодического процессов в колебательном контуре.

Используемая литература

[1] § 28.1;

[2] § 19.6;

[3] §13.3;

[4] § 146.

Лабораторная работа 2-14

Изучение электрических процессов в простых линейных цепях при действии гармонической электродвижущей силы (фпэ-09)

Цель работы: изучение электрических процессов в цепях, состоящих из последовательно соединенных элементов: а) двух резисторов (цепь RR), б) резистора и конденсатора (цепь RC), в) резистора и катушки индуктивности (цепь RL):

а) измерение коэффициента передачи цепей RR, RC, RL; изучение зависимости коэффициента передачи цепей RC и RL от частоты входного сигнала;

б) оценка параметров цепей R, C, L;

в) определение разности фаз между колебаниями тока в изучаемых цепях и входным напряжением.

Теоретическое введение

Цепь переменного электрического тока представляет собой ряд соединенных между собой в той или иной последовательности элемен­тов, в которых возбуждаются токи одним или несколькими источниками ЭДС.

Все элементы электрической цепи обладают сопротивлением. Это сопротивление может быть двух видов: активное или реактивное. Если при прохождении тока через элемент происходит только необратимое превращение электрической энергии в теплоту, то его сопротивление называют активным. Если же подобной потери электрической энергии не происходит, сопротивление элемента называют реактивным.

Элемент цепи с активным сопротивлением называется резистором. Реактивным сопротивлением – ёмкостным и индуктивным – обладают соответственно конденсаторы и катушки индуктивности.

Элементы цепи называются идеальными, если они обладают только одним видом сопротивления – активным, ёмкостным или индуктивным. Для идеальных элементов справедливы соотношения:

; (14.1)

; (14.2)

; , (14.3)

где – сопротивление резистора;– емкость конденсатора; – индуктивность катушки; ,, – падения напряжения (или просто напряжения) на соответствующих элементах; – ток через элемент;– заряд конденсатора;– ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через неё переменного тока.

Элементы цепи могут быть линейными и нелинейными. Если сопротивление элемента не зависит от величины тока в цепи или от напряжения на элементе, то такой элемент называется линейным. Электрические цепи, составленные из линейных элементов, также называются линейными. В линейных цепях электрические процессы описываются линейными алгебраическими или дифференциальными уравнениями. Этому условию, например, отвечают выражения (14.1)÷(14.3). Электрические процессы в линейных цепях называются установившимися (стационарными), если закон изменения всех токов и напряжений совпадает с точностью до постоянной величины с законом изменения внешней ЭДС, действующей в цепи. Если это условие не выполняется, процессы называются переходными.

При анализе электрических процессов в цепях переменного тока к мгновенным значениям тока можно применять законы Ома и Кирхгофа и другие правила, установленные для постоянного тока, если переменный ток является квазистационарным. Условие квазистационарности означает, что мгновенные значения переменного тока практически одинаковы на всех участках цепи. Это условие выполняется для медленно меняющегося тока, когда его мгновенное значение не успевает измениться за время распространения электрического процесса вдоль цепи. Если – характерное время изменения мгновенного значения тока, а – время распространения электрического процесса вдоль цепи протяженностьюсо скоростью(равной по порядку величины скорости распространения электромагнитного возмущениям/с), то условие квазистационарности запишется в виде:.

В дальнейшей будем полагать, что элементы цепи являются идеальными и, в соответствии с соотношениями (14.1)÷(14.3), линейным. Электрические процессы будем считать установившимися, а переменные токи – квазистационарными.

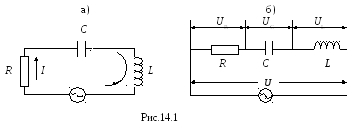
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора R, емкости C и индуктивности L (рис.14.1).

Допустим, что источник переменной ЭДС (генератор) не обладает внутренним сопротивлением и создает на входе цепи напряжение U, равное его ЭДС . Такое допущение всегда можно сделать, включив сопротивление генератора в состав рассматриваемой электрической цепи.

Положим далее, что ток в цепи

(14. 4)

создается в стационарном состоянии генератором с гармонической ЭДС

, (14. 5)

где – круговая частота колебаний ЭДС и тока; – период колебаний; – угол сдвига фазы напряжения (ЭДС) относительно фазы тока; – амплитуда ЭДС; – амплитуда тока.

Найдем, чему равны амплитуда тока и сдвиг фаз , если известны параметры цепи, ,, и уравнение для ЭДС (14.5).

Одновременно определим, какой вид имеет величина , равная отношению амплитуды ЭДС к амплитуде тока: .

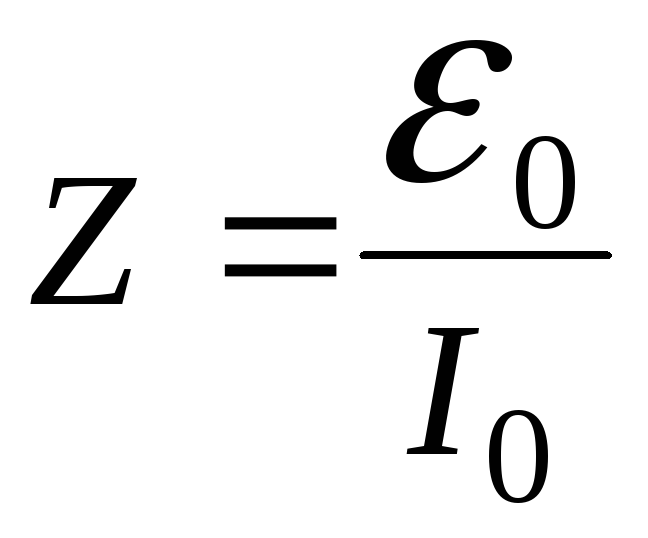Эта величина (по аналогии с законом Ома для замкнутой цепи постоянного тока) называется полным сопротивлением цепи переменного тока. На основании второго правила Кирхгофа для контура на рис.14.1,а можем записать 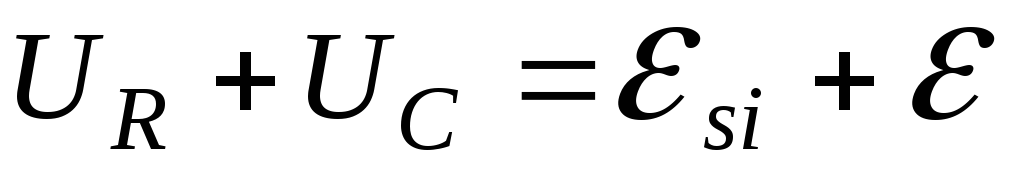или (рис. 14.1,б):

, (14.6)

то есть сумма напряжений на отдельных элементах контура равна в каждый момент времени внешней ЭДС, действующей в контуре.

Учитывая соотношения (14.1)÷(14.3), имеем

, (14.7)

или, с учетом (14.5) и того, что :

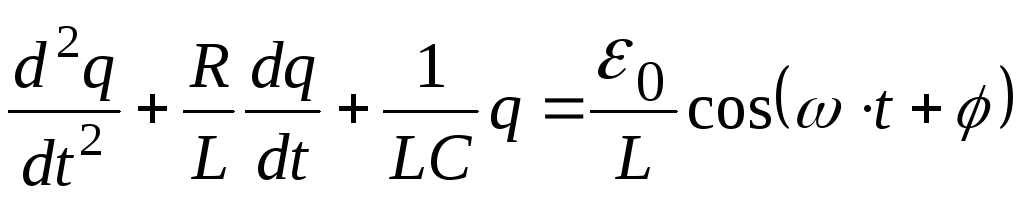. (14.7а)

Выражение (14.7а) представляет собой дифференциальное уравнение вынужденных колебаний. Подстановка в уравнение (14.7) выражений (14.4), (14.5) и выполнение операций интегрирования и дифференцирования приводит это уравнение к виду:

Используя далее соотношения

, ,

окончательно получим:

(14.8)

Из уравнения (14.8) можно сделать ряд выводов.

Выпишем из этого уравнения выражения для напряжений ,,и рассмотрим их совместно с выражением (14.4) для тока:

, где , (14.9а)

, где (14.9б)

, где . (14.9в)

Сравнивая фазы напряжений ,ис фазой тока, видим, что:

1) напряжение на резисторе совпадает по фазе с током;

2) напряжение на емкости отстает по фазе от тока на угол ;

3) напряжение на индуктивности опережает по фазе ток на угол .

Далее найдем отношения амплитуд напряжений , ,к амплитуде тока :

; ;. (14.10)

Формулы (14.10) определяют величины, которые называются соответственно активным, реактивным ёмкостным и реактивным индуктивным сопротивлениями. Емкостное сопротивление обозначается через , индуктивное – через . Из формул (14.10) следует, что активное сопротивление цепи переменного тока равно сопротивлению цепи для постоянного тока, то есть омическому сопротивлению , реактивные же сопротивления:

; (14.11)

Перейдем к основной задаче: нахождению выражений, определяющих амплитуду тока , сдвиг по фазе напряжения (ЭДС) и тока и полное сопротивление цепи, изображенной на рис. 14.1.

Уравнение (14.8) позволяет решить эту задачу, при этом методы решения могут быть различные. Воспользуемся графическим способом представления гармонических колебаний – методом векторных диаграмм. В этом методе гармоническим величинам (напряжениям, токам) сопоставляются вращающиеся векторы. Для этого на плоскости выбирают произвольное начало координат 0 и проводят ось X. Изучаемую гармоническую величину изображают вектором, построенным из начала координат. Длина вектора равна (в выбранном масштабе) амплитуде гармонической величины, а угол между вектором и осью X равен углу начальной фазы. Вектор равномерно вращается вокруг точки 0 с угловой скоростью в направлении против часовой стрелки. При этом проекция вектора на ось Х в любой момент времени равна мгновенному значению гармонической величины, изменяющейся со временем по закону косинуса.

В соответствии со сказанным левую часть уравнения (14.8) можно рассматривать как сумму проекций векторов, изображающих напряжения ,и, а правую часть – как проекцию вектора, изображаю­щего суммарное напряжение . Поскольку при сложении векторов сумма проекций слагаемых равна проекции суммы, то можно найти геометрическую сумму векторов, изображающих напряжения,,и приравнять эту геометрическую сумму вектору, изо­бражающему напряжение. Другими словами, вместо алгебраическо­го равенства (14.8) можно рассматривать векторное равенство

, (14.12)

причем модули векторов ,,определяются равенствами (14.9). Такое представление значительно упрощает нахождение амплитуды и сдвига фаз . На рис. 14.2 построены векторные диаграммы для момента време­ниt=0, соответствующие уравнениям (14.8) и (14.12).

Из рис. 14.2 следуют соотношения:

и .

Поскольку векторы инаправлены противоположно, и, тогда, с учетом (14.12):

, (14.13)

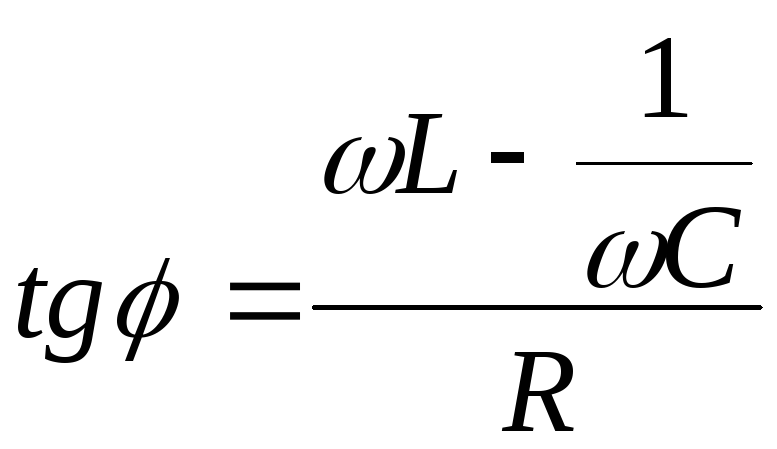, (14.14)

откуда

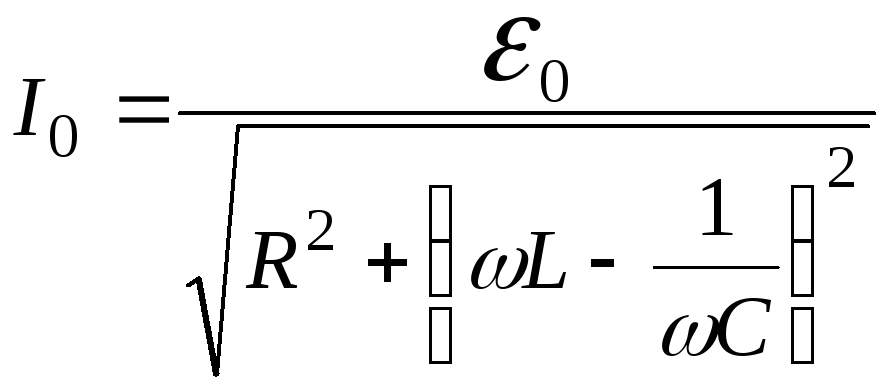, (14.15)

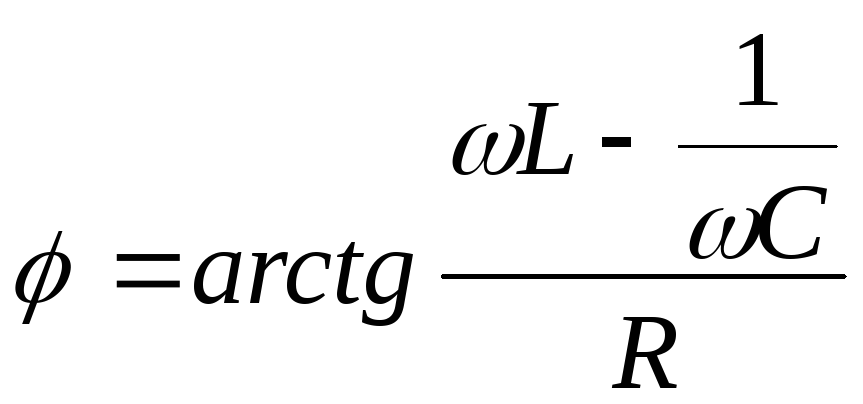, (14.16)

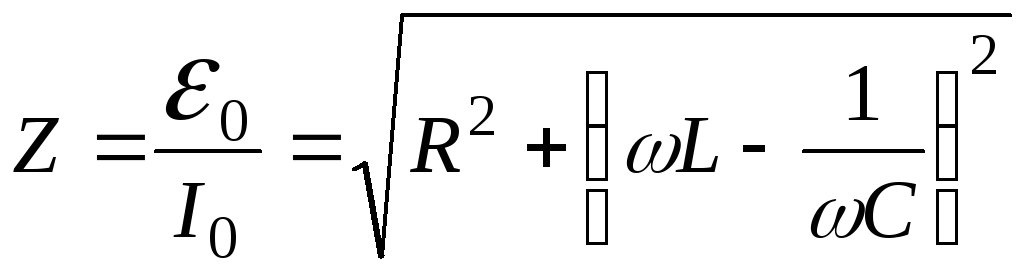. (14.17)

Видим, что колебания тока в цепи отстают по фазе от колебаний ЭДС на угол , зависящий от частоты и определяемый уравнением (14.16). Можно также сказать, что напряжение во внешней цепи, содержащей последовательно соединенные ,и, опережает по фазе ток на угол , определяемый выражением (14.16). Полное сопротивление цепи , в соответствии с (14.17), также зависит от частоты и может быть записано в виде:

, (14.18)

где – полное реактивное сопротивление цепи. Из формулы (14.18) следует, что активное и реактивное сопротивления цепи складываются геометрически.