Tom_1_Obschestvennoe_zdorovye_Kucherenko

ревматологических кабинетов в поликлиниках позволяет снизить сроки обследования больных ревматизмом.

2.6. СРЕДНИЕ ВЕЛИЧИНЫ. ХАРАКТЕРИСТИКИ

РАЗНООБРАЗИЯ ПРИЗНАКА

При изучении общественного здоровья и деятельности учреждений здравоохранения, проведении клинических и лабораторных исследований получаемые количественные результаты бывают весьма многочисленны и одновременно малопригодны для анализа без их предварительной обработки. Для получения представления о размерах изучаемых признаков (например, роста детей разного возраста, скорости оседания эритроцитов при разных заболеваниях, нагрузки врачей разных специальностей и др.), чтобы судить об особенностях и закономерностях изучаемых явлений, необходимо узнать их обобщающие характеристики в виде средних величин и критериев разнообразия. Однако сначала материалы исследования требуется систематизировать, сделать более доступными для последующих вычислений, т.е. нужно представить полученные данные в виде так называемого вариационного ряда.

Вариационный ряд — ряд числовых значений признака (вариант), расположенных в убывающей или возрастающей последовательности с соответствующими им частотами. Вариантой называют каждое количественное выражение признака, изменения которого подлежат изучению. Варианту обозначают буквой х (в некоторых руководствах — буквой V ). Частота (р) — численность («вес») отдельных вариант в совокупности. Частота показывает, сколько раз данная варианта встречается в вариационном ряду. Общее количество наблюдений, из которых состоит вариационный ряд, обозначают буквой n (то есть это сумма всех частот: n = Σр).

Если в вариационном ряду каждую варианту встречают только один раз (р = 1), такой ряд называют простым. Во взвешенном ряду отдельные варианты повторяются неоднократно и с разной частотой. При большом количестве наблюдений (n >30) такой ряд целесообразно сгруппировать, т.е. объединить в группы соседние варианты. При составлении сгруппированного ряда должны быть выполнены следующие требования:

– все варианты распределения должны войти в группы;

–интервалы в группах должны быть одинаковыми;

–каждой группе присваивают частоту, равную сумме частот всех вариант, вошедших в данную группу;

–количество групп определяют в зависимости от силы наблюдений (обычно от 7 до 15 групп).

После того как вариационный ряд построен, приступают к его обработке. Она заключается в нахождении средней величины, среднеквадратичного отклонения и других параметров ряда.

Средняя величина — обобщающая характеристика размера изучаемого признака. Она позволяет одним количеством дать представление о всей совокупности качественно однородных признаков. Она как бы выражает то общее, что характерно для признака в данной совокупности. Различают несколько видов средних величин: среднеарифметическую, среднюю геометрическую, среднюю гармоническую. Иногда в качестве обобщающих величин используют моду

имедиану. Мода (Мо) — наиболее часто встречаемая в данном ряду варианта. Медиана (Ме) — значение варианты, делящей вариационный ряд пополам. Мода и медиана выражают основную центральную тенденцию изучаемого признака, на них не оказывают влияния значения крайних вариант.

Наиболее употребимой на практике служит среднеарифметическая. Ее обозначают буквой М. В простом вариационном ряду ее находят путем суммирования всех вариант и деления полученной суммы на общее количество наблюдений (М = Σх/n). Это простая среднеарифметическая. Среднеарифметическую взвешенную вычисляют по формуле: М = Σхр/n, т.е. значения вариант перемножают с частотами, сумму этих произведений делят на количество наблюдений (n = Σр). Важно отметить, что вариационные ряды бывают дискретными (прерывными) и непрерывными. В дискретных рядах числовые значения признака выражены только целыми числами (например, количество посещений, частота пульса, количество детей в семье и др.). Непрерывные ряды составляют варианты, выраженные любыми величинами, в том количестве дробными (например, рост, масса и температура тела

идр.). Эти различия следует учитывать при обработке сгруппированных вариационных рядов. Все расчеты в таких рядах ведут от центральной варианты, т.е. среднего значения в своей группе вариант (от середины интервала). Если это дискретный (прерывный) ряд, то центральную варианту вычисляют как полусумму начальной и конечной варианты в группе. Если это непрерывный

Среднеарифметическая показывает то типичное, что характерно для всей совокупности. Она позволяет обнаружить общие черты, существующие закономерности, поскольку с ее помощью можно получить представление о наиболее общих особенностях всех вариант изучаемой группы. Среднеарифметическая имеет ту же размерность, что и каждая из вариант.

Для среднеарифметической характерен ряд свойств:

–она имеет обобщающий характер и абстрактное значение (например, даже в прерывном ряду она может иметь дробные значения);

–сумма всех (положительных и отрицательных) отклонений отдельных вариант от средней равна 0 (это свойство используют при проверке правильности расчетов средней);

–сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, не равной средней;

–сумма произведений отдельных вариант на свои частоты равна произведению средней на количество наблюдений;

–если каждую из вариант увеличить или уменьшить на определенное количество (в определенное количество раз), то среднеарифметическая увеличится или уменьшится на столько же (во сколько же) раз.

Последнее свойство используют в тех случаях, когда варианты представлены очень малыми или, наоборот, большими числами.

Если вариационный ряд представлен дробями, в знаменателях которых находятся варианты ряда (например, коли-титр), определяют среднюю гармоническую:

Мгарм. = n/Σ(р / х).

Среднюю геометрическую вычисляют, когда изменение (вариация) членов данного статистического ряда происходит не путем арифметического прибавления какой-либо величины, а в геометрической прогрессии, путем умножения на определенный множитель. Вычисление средней проводят с помощью логарифмов:

lgМгеом. = Σр lgх / n.

Получив lgхгеом., путем потенцирования определяют величину средней геометрической.

Средняя величина, безусловно, является важной характеристикой совокупности, однако для более полного суждения о ней необходимо оценить также изменчивость изучаемого признака. Если вариационный ряд более компактен и менее рассеян, отдельные варианты расположены вблизи средней, то эта средняя лучше характеризует данную совокупность. Наоборот, если ряд растянут, отдельные значения отклоняются далеко от средней, т.е. имеется выраженная вариабельность признака, можно сказать, что средняя хуже отражает в целом свой ряд. Таким образом, кроме средней величины необходима вторая важная характеристика вариационного ряда — степень его колеблемости.

В определенной мере о колеблемости, разнообразии признака можно судить по амплитуде ряда, т.е. по разнице между наибольшей

(хmax) и наименьшей (хmin) вариантами (А = хmax – хmin). Например, при подсчете пульса в двух группах рабочих средняя частота пуль-

са оказалась одинаковой и составила 69 в мин. При этом в первой группе амплитуда была 10 ударов (хmax — 74, хmin — 64), а во второй — 22 удара (соответственно 80 и 58). Амплитуда в первой группе значительно меньше, и, следовательно, варианты в большей степени группируются вокруг средней, а значит, ряд менее рассеян.

В то же время амплитуда учитывает только разнообразие крайних вариант ряда, она не позволяет получить информацию о разнообразии признака в совокупности с учетом ее внутренней структуры. Именно поэтому этим критерием можно пользоваться только для очень приблизительной оценки разнообразия, в частности, при малом количестве наблюдений (n ≤30).

Наиболее полную характеристику разнообразия признака в совокупности дает так называемое среднеквадратичное отклонение, или сигма (σ). Сигма — мера колеблемости, вариабельности признака. Для ее вычисления необходимо найти отклонения (d) каждой варианты от средней, возвести их в квадрат (d2), перемножить квадрат отклонения на частоту каждой варианты (d2р), получить сумму этих произведений (Σd2р), в затем рассчитать сигму по формуле:

σ = √(∑d2p) / n;

при малом количестве наблюдений (n <30) используют формулу:

σ = √(∑d2p) / n – 1.

Пример расчета основных характеристик вариационного ряда представлен в табл. 2-18.

Таблица 2-18. Распределение больных терапевтического отделения по длительности пребывания в стационаре

М = Σхр / n = 1710 / 90 = 19 дней.

Среднее значение отклонения (σ) показывает, на какую величину в данном вариационном ряду каждая из вариант в среднем отличается, отклоняется от среднеарифметической ряда. Чем больше выражены эти отклонения, т.е. чем больше сигма, тем вариационный ряд более разнообразен, рассеян, а среднеарифметическая, соответственно, менее представительна, и наоборот. Именно поэтому сигма служит не только мерой колеблемости ряда, но одновременно и мерой типичности средней величины данного ряда, ее способности представлять изучаемую совокупность, быть ее полноценной обобщающей характеристикой, т.е., по существу, выполнять свое назначение.

Это положение позволяет использовать сигму при сопоставлении вариационных рядов с одинаковой размерностью для сравнительной оценки типичности средних величин. Например, в двух городах — А и Б средний рост 6-летних девочек был примерно одинаков (соот-

ветственно 120,2 и 120,4 см), а сигмы заметно отличались (в городе А —

±4 см, в городе Б — ±6 см). Можно сказать, что в городе А рост девочек менее вариабелен, а средняя (120,2 см) более типична и лучше характеризует свою совокупность, нежели средняя (120,4 см) в городе Б.

Нередко приходится сопоставлять вариационные ряды с неодинаковой размерностью (например, рост, массу тела, уровень артериального давления и др.). Для того чтобы определить устойчивость и колеблемость этих признаков и оценить типичность средних величин в таких рядах, воспользоваться сигмами напрямую не удастся: их величины несопоставимы (действительно, невозможно сравнить килограммы с сантиметрами). В таких случаях необходимо вычислить коэффициент вариации (Сv). Он служит относительной мерой разнообразия, и рассчитывают его как процентное отношение среднеквадратичного отклонения (σ) к среднеарифметической величине (М):

Сv = σх100 / М.

В табл. 2-19 дан пример сравнения антропометрических данных (роста, массы тела и жизненной емкости легких) 10-летних мальчиков.

Таблица 2-19. Антропометрические данные 10-летних мальчиков

Видно, что рост наиболее стабилен у мальчиков данного возраста (Сv = 12,5%).

Для ориентировочной оценки полученных результатов надо учитывать, что величина коэффициента менее 10% свидетельствует о слабом разнообразии признака. Такой вариационный ряд считают однородным, а среднюю — типичной. Значение коэффициента вариации от 10 до 20% говорит о средней степени колеблемости, а при Сv больше 20% отмечают сильное разнообразие признака. Такой ряд обладает значительной вариабельностью, к средней величине такого ряда следует относиться с сомнением как малотипичной.

К помощи коэффициента вариации прибегают и при необходимости сравнивать вариационные ряды хотя и с одной размерностью,

но с резкой разницей в значениях вариант и величины среднеарифметической. Например, необходимо оценить степень разнообразия массы тела у новорожденных и 10-летних мальчиков. Понятно, что у новорожденных сигма всегда будет меньше, поскольку значительно меньше их индивидуальная масса тела. В этом случае следует ориентироваться не на среднеквадратичное отклонение, а на относительную меру разнообразия — коэффициент вариации (табл. 2-20).

Таблица 2-20. Данные о массе тела мальчиков

Из табл. 2-18 следует, что у новорожденных колебания массы тела гораздо меньше выражены, чем у 10-летних детей.

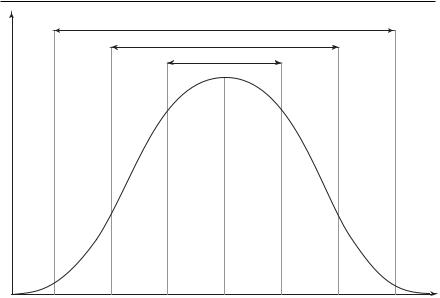
Возможность практического использования среднеквадратичного отклонения связана также с его ролью в формировании структуры вариационного ряда. Теорией статистики доказано, что в вариационных рядах, соответствующих нормальному распределению признака (а ему подчиняется большинство признаков в биологии и медицине), в пределах М±1σ находятся 68,3% наблюдений, в пределах М±2σ — 95,5%, а в пределах М±3σ — 99,7% всех случаев, составляющих совокупность. Таким образом, интервал М±3σ охватывает практически весь вариационный ряд (правило трех сигм) (рис. 2-9).

Вмедицине это правило применяют для суждения о норме

ипатологии. Отклонение параметра (например, уровня сахара в крови) от его среднеарифметической в пределах от –1 до –2σ и от +1 до +2σ, а значения сверх –2σ или +2σ относят к патологии.

Использование правила трех сигм позволяет также восстановить частотную характеристику вариационного ряда (реконструировать ряд). Зная среднюю величину и среднеквадратичное отклонение, можно, прежде всего, ориентировочно определить крайние

значения вариант. Например, средний рост 10-летних мальчиков составляет 140 см при σ = ±5 см. Утроенная сигма равна 15 см. Следовательно:

хmin = М – 3σ = 140 – 15 = 125 см;

хmax = 140 + 15 = 155 см.

Амплитуда ряда составляет:

155 – 125 = 30 см.

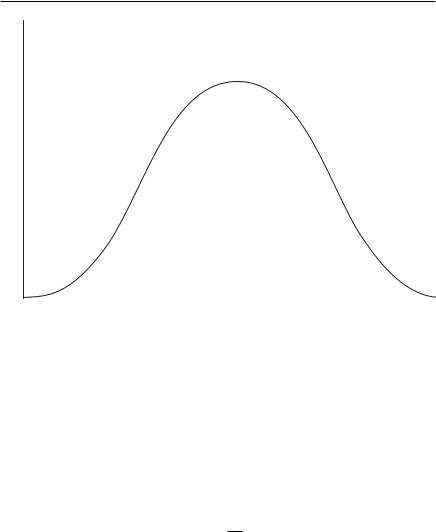
Далее определяют количества частот в определенных интервалах ряда. Если в пределах М±1σ находится 68,3% вариант, то на интервал х–1σ приходится 34,15%, столько же — на интервал М+1σ. Поскольку в пределах х±2σ находится 95,5% вариант, а в пределах М±1σ — 68,3%, то на интервал –1σ...–2σ и +1σ...+σ2 приходится: 95,5–68,2=27,2%, а на каждый из них — по 13,6%. Аналогично вычисляют значения последних интервалов, на каждый из которых приходится по 2,1% вариант ряда (рис. 2-10).

Если, например, требуется обеспечить 1000 мальчиков в возрасте 10 лет одеждой или обувью необходимых размеров, это делают исходя из полученных процентильных соотношений.

Глава 2. Основные статистические методы обработки результатов... 103

%

Рис. 2-10. Структура вариационного ряда роста 10-летних мальчиков

Еще одна сфера применений среднеквадратичного отклонения — педиатрия и гигиена детей и подростков. Здесь ее используют для составления и оценки индивидуального профиля физического развития ребенка (подростка) на основе стандартных сигмальных характеристик антропометрических признаков.

Наконец, сигма является важным компонентом формулы расчета ошибки репрезентативности среднеарифметической:

σ

m = √n.

Ошибка репрезентативности необходима для оценки достоверности результатов исследования.