3.2 Уравнение Гюи – Стодолы

Если тело или газ изотермически поглощает положительное количество теплоты при температуреТ, тогда изменение его энтропии задается уравнением:

(9)

Используя это выражение, можно переписать правую часть уравнения (8а) следующим образом:

(10)

где ∆S – изменение энтропии теплообменника. При адиабатическом процессе одновременного изменения энтропии окружающей среды не происходит 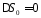, и, следовательно, второй закон может быть формально представлен так:

(11)

что, в свою очередь, позволяет представить уравнения (10) в виде:

(12)

Последнее достаточно простое соотношение между величиной потерь полезной работы и увеличением энтропии в ходе процесса носит название уравнения Гюи – Стодолы.

Из инженерной практики известно, что количество передаваемой в теплообменнике теплоты пропорционально разности температур и поверхности теплообмена. Но, как только что установлено,, а не ∆Т, является движущей силой потока теплоты. Поэтому в первом приближении можно записать:

(13)

где – общий термодинамический коэффициент теплопереноса,А – поверхность теплообменника. Подставив данное выражение в уравнение (8), можно получить:

(14)

Последнее уравнение свидетельствует о том, что величина потерь пропорционально квадрату движущей силы. С другой стороны, из уравнения (13) следует, что в случае передачи теплоты Q, стремление инженера уменьшить движущую силу (чтобы уменьшить потери) должно компенсироваться или материалом теплообменника с более высокой теплопроводностью (т.е. большим значением ), или большей поверхностью теплообменника. Указанные зависимости отражают экономическую необходимость одновременного проведения оптимизации стоимости оборудования и стоимости энергии.

3.3 Задача производства энтропии в общем виде

Рассмотрим задачу производства энтропии в более общем виде, для чего представим установившийся поток, который выполняет работу (рис. 12). Теплообмен происходит только с окружающей средой при температуре. Принимается, что поток не подвергается значительным изменениям скорости или высоты, т.е. макроскопическими изменениями кинетической и потенциальной энергии можно пренебречь.

Рисунок 12 - Выполнение работы и обмен теплотой с окружающей средой при переходе рабочей жидкости из состояния 1 в состояние 2.

Первый закон термодинамики для рассматриваемой системы имеет вид:

(15)

Второй закон представлен, как и ранее:

(16)

Объединив эти уравнения, используя известное соотношение:

(17)

а также, исключая и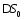, выведем следующее уравнение:

(18)

где ∆H и ∆S выражают изменения энтальпии и энтропии потока при переходе из состояния 1 в состояние 2, например:

(19)

Очевидно, что минимальное количество работы, необходимое для совершения данного изменения в указанных условиях, задается уравнением:

(20)

Согласно второму закону, ; тогда реальное количество затраченной работы будет больше:

(21)

Количество потерь определяется так:

(22)

что приводит к тому же уравнению Гюи – Стодолы:

(23)

Соотношение (23), выполняется для общего обмена теплотой и работой между средой потока и ее окружением. Обобщенная формулировка второго закона

(24)

находит здесь ясную и недвусмысленную формулировку с позиции хорошо известных переменных – давления и температуры.

Фактор Карно количественно выражает, какая доля теплоты превращается в полезную работу. Теплота самопроизвольно переходит от более нагретой зоны к менее нагретой и доля теплоты, способной превратиться в полезную работу, падает. Качество теплоты определяется как ее наибольший потенциал для совершения работы по отношению к определенной окружающей среде. Обычно это среда, внутри которой протекает процесс. Полностью теплота теряет способность совершать работу при температуре, равной температуре окружающей среды.