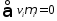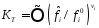- •Н.В. Лисицын
- •Содержание
- •1 Ресурсы и ресурсосберегающие технологии
- •1.1 Устойчивое развитие, жизненный цикл
- •1.2 Критерии оценки больших систем
- •1.3 Ресурсосбережение
- •2 Основные термодинамические приложения для анализа химико-технологических систем
- •2.1 Энтропия и ее производство
- •2.2 Первый и второй законы термодинамики. Производство энтропии.
- •2.3 Изменение состава систем. Энтропия процессов смешения и химического превращения
- •2.4 Коэффициент полезного действия систем
- •3 Эффективность карно и потери полезной работы систем
- •3.1 Потребление полезной работы
- •3.2 Уравнение Гюи – Стодолы
- •3.3 Задача производства энтропии в общем виде
- •4. Причины и следствия увеличения энтропии систем
- •4.1 Движущие силы и потоки
- •4.2 Феноменологические законы
- •4.3 Принцип симметрии кинетических коэффициентов
- •4.4 Ограниченность применения линейных законов тепло – и массопереноса
- •5. Энергетические потери и неравновесность
- •5.1 Внутренне обратимый двигатель Карно
- •5.2 Принцип равномерного распределения энергии
- •5.3 Прямоточный и противоточный процессы теплообмена
- •6 Эксергия и эксергетический баланс процесса
- •6.1 Эксергия, энергия Гиббса и полезность
- •6.2 Эксергетический баланс
- •6.3 Физическая эксергия. Эксергия смешения
- •6.4 Качество источников энергии
- •7. Физическая и химическая эксергия
- •7.1 Эксергия компонентов воздуха
- •7.2 Химическая эксергия соединений
- •7.3 Энергия Гиббса образования и химическая эксергия
- •8 Эксергетический и энергетический анализ и балансы
- •8.1 Основные недостатки энергетического анализа систем
- •8.2 Уравнения баланса массы, энергии, эксергии и энтропии
- •9 Анализ процессов производства электроэнергии
- •9.1 Основные процессы производства энергии
- •9.2 Сжигание угля и газа
- •9.3 Термодинамическая эффективность газового цикла
- •9.4 Эффективности парового цикла
- •9.5 Эффективность объединенного цикла
- •10 Анализ процессов разделения
- •10.1 Однократная равновесная перегонка бинарной смеси
- •10.2 Термодинамический анализ идеальной дистилляционной колонны
- •10.3 Анализ реальной колонны
- •11 Анализ химико-технологических систем. Основные правила ресурсосбережения
- •11.1 Процедура анализа систем
- •11.2 Эвристические правила экономии материальных и энергетических ресурсов
- •4. Если химическая реакция протекает с выделением тепла, необходимо ее начинать при повышенной (не при пониженной) температуре (рис.49).
- •12 Методические рекомендации по выполнению контрольных работ
- •13 Контрольные работы
- •13.1 Контрольная работа №1
- •13.2 Контрольная работа №2
- •13.3 Контрольная работа №3
- •Кафедра ресурсосберегающих технологий
- •Теоретические основы энерго- и ресурсосбережения
- •190013, Санкт-Петербург, Московский пр., 26
2.3 Изменение состава систем. Энтропия процессов смешения и химического превращения
В отличии от систем постоянного состава, где могут изменяться давление Р, температура Т или агрегатное состояние, изменения состава скорее являются правилом, чем исключением в реальных технических системах. Гомогенные фазы могут смешиваться, а гетерогенные смеси могут расслаиваться на фазы. Гомогенная или гетерогенная смесь может самопроизвольно распасться на один или несколько продуктов. Во всех этих случаях имеют место изменения в составе. При этом рассматриваются:
 – энергия
Гиббса i-ого
вещества или химический потенциал
индивидуального соединения,
– энергия
Гиббса i-ого
вещества или химический потенциал
индивидуального соединения,
 – летучесть
(фугитивность)
–
термодинамическая величина, служащая
для описания свойств реальных газовых
смесей. Позволяет применять уравнения,
выражающие зависимость химического
потенциала идеального газа от температуры,
давления и состава системы, к компоненту
газовой смеси, если заменить в этих
уравнениях парциальное давление на
летучесть.
– летучесть
(фугитивность)
–
термодинамическая величина, служащая
для описания свойств реальных газовых
смесей. Позволяет применять уравнения,
выражающие зависимость химического
потенциала идеального газа от температуры,
давления и состава системы, к компоненту
газовой смеси, если заменить в этих
уравнениях парциальное давление на
летучесть.
 – активность
–
термодинамическая величина, позволяющая
представлять в удобной для практического
использования форме концентрационную
зависимость химических потенциалов
компонентов реального раствора. С ее
помощью можно применять к реальному
раствору термодинамические соотношения,
относящиеся к идеальному раствору, если
заменить в них концентрации активностями.
– активность
–
термодинамическая величина, позволяющая
представлять в удобной для практического
использования форме концентрационную
зависимость химических потенциалов
компонентов реального раствора. С ее
помощью можно применять к реальному
раствору термодинамические соотношения,
относящиеся к идеальному раствору, если
заменить в них концентрации активностями.
Если происходят процессы смешения или химического превращения, самопроизвольно или в результате приложенной к системе работы, процесс, как было отмечено, будет протекать с увеличением энтропии:
|
|
(9) |
и общая энтропия будет стремиться к наибольшему значению, которое может быть достигнуто в состоянии равновесия.
Действительно, для различных молекул, которые близки друг другу, например, изомеры или молекулы приблизительно одного и того же размера, полярности или обладающие другими схожими параметрами, термодинамическая вероятность существования их в виде смеси при равных значениях Р и Т значительно больше, чем вероятность существования в виде чистых веществ (в мольных единицах):
|
|
(16) |
где
 .
.
Если происходит только изменение состава при постоянных Р и Т и оно ограничено рассматриваемой системой, например, смесью, разделительной колонной или реактором, то энергия Гиббса системы может быть определена следующим образом:
|
|
(17) |
С течением времени при постоянном давлении и температуре энергия Гиббса стремится к минимальной величине, которая будет достигнута, когда система придет к состоянию равновесия (рис. 5):
|
|
(18) |
или
|
|
(19) |

Рисунок 5 - Изменение энергии Гиббса при стремлении системы к равновесию
Если рассматривается химическая реакция, которая протекает в гомогенной смеси, то равновесный состав смеси может быть найден из равенства (19), если известна зависимость величины G от состава.
Если процесс смешения происходит с пренебрежимо малым изменением внутренней энергии U и объема V, его можно считать идеальным смешением, и в этом случае можно показать, что для 1 моля смеси
|
|
(20) |
 – мольная
доля компонента i
в смеси, R
– универсальная газовая постоянная.
Для идеальной смеси
– мольная
доля компонента i
в смеси, R
– универсальная газовая постоянная.
Для идеальной смеси
 и
и равны нулю при смешивании при постоянныхР
и Т,
поэтому
равны нулю при смешивании при постоянныхР
и Т,
поэтому
 задается выражением:
задается выражением:
|
|
(21) |
 также
равно нулю и, таким образом, принимая
во внимание уравнение (3), идеальное
смешение при постоянных давлении и
температуре будет протекать без тепловых
эффектов.
также
равно нулю и, таким образом, принимая
во внимание уравнение (3), идеальное
смешение при постоянных давлении и
температуре будет протекать без тепловых
эффектов.
Для
описания отклонений от идеальности
используется свойство избыточности и,
соответственно, избыточные термодинамические
функции
 ,
которые в общем виде могут быть
представлены так:
,
которые в общем виде могут быть
представлены так:
|
|
(22) |
Наряду
с другими, наиболее часто рассматривается
избыточность энергии Гиббса
 .
Разработано много моделей для описания
и предсказания величины
.
Разработано много моделей для описания
и предсказания величины на основании свойств молекул смеси и
их взаимодействий. Модели
на основании свойств молекул смеси и
их взаимодействий. Модели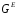 часто относятся к конденсированным
состояниям – твердой и жидкой фазам.
часто относятся к конденсированным
состояниям – твердой и жидкой фазам.
В случае значительного изменения объема при смешении или разделении в отличии от энергии Гиббса принято рассматривать другую термодинамическую функцию – энергию Гельмгольца А, которая определяется как:
|
|
(23) |
а
ее свойство избыточности
 является более предпочтительным при
описании указанных процессов. Для этого
необходимо иметь уравнение состояния,
которое выражает объемное поведение
смеси как функцию давления, температуры
и состава.
является более предпочтительным при
описании указанных процессов. Для этого
необходимо иметь уравнение состояния,
которое выражает объемное поведение
смеси как функцию давления, температуры
и состава.
Парциальные молярные функции играют важную роль в термодинамике смесей и фазовых равновесиях. Они определяются следующим образом:

|
|
(24)
|
Наиболее
известный пример – парциальная молярная
энергия Гиббса, которая более известна
как термодинамический потенциал
 .
.
Термодинамический
потенциал i-того
компонента гомогенной смеси определяется
как:
|
|
(25) |
Важное условие фазового равновесия можно записать так:
|
|
(26) |
Или, используя летучесть компонентов смеси:
|
|
(27) |
В этих уравнениях штрихи указывают на соответствующую фазу. Летучесть и активность напрямую связаны с термодинамическим потенциалом, который имеет размерность Дж/моль, в то время как f имеет размерность давления, а активность является величиной безразмерной.
Последнее уравнение в приложении к равновесию жидкость – пар записывается в виде
|
|
(28) |
и
сводится к закону Рауля для идеальных
газов, для которого коэффициенты
летучести
 и
и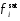 равны 1, и рассматривается идеальное
смешение жидкостей, для которого
коэффициент активности
равны 1, и рассматривается идеальное
смешение жидкостей, для которого
коэффициент активности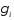 и фактор Пойнтинга (экспонента в уравнении
(28), где
и фактор Пойнтинга (экспонента в уравнении
(28), где – молярный объем жидкой фазы) равны 1.
– молярный объем жидкой фазы) равны 1.
Закон Рауля:
|
|
(29) |
Коэффициент летучести может быть вычислен из соответствующего уравнения состояния; коэффициент активности может быть выведен из применяемого на практике выражения для GE.
Активность
зависит от температуры Т
и концентрации
 .
.
Функция, определяемая уравнением (17), – энергия Гиббса G – играет важную роль в описании, с одной стороны, межфазных переходов, когда частицы остаются теми же самыми, но иначе распределяются между имеющимися фазами, такими как пар и жидкость, с другой стороны – при описании изменений, когда частицы меняют свою природу, т.е. происходит химическая реакция. Химические реакции и фазовые переходы в равной мере протекают в направлениях, удовлетворяющих уравнениям (18) и (19).
Для химической реакции:
|
vAA+ |
(30) |
где
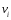 –
стехиометрический коэффициент,
соответствующий частице i,
считающийся положительным для продукта
реакции и отрицательным для реагента.
Ее протекание характеризуется свойством,
которое называется степенью полноты
реакции:
–
стехиометрический коэффициент,
соответствующий частице i,
считающийся положительным для продукта
реакции и отрицательным для реагента.
Ее протекание характеризуется свойством,
которое называется степенью полноты
реакции:
|
|
(31) |
Скорость протекания реакции:
|
|
(32) |
В состоянии равновесия (рис. 6):
|
|
(33) |
и
|
|
(34) |

Рисунок 6 - Изменение энергии Гиббса G в зависимости от степени полноты реакции
Если известна зависимость величины G от состава, положение химического равновесия может быть определено с помощью уравнения (33), которое используется для нахождения равновесного состава смеси.
Можно показать, что химическое равновесие характеризуется уравнением:
|
|
(35) |
Константа химического равновесия при температуре Т задается выражением:
|
|
(36) |
и может быть определена согласно известного соотношения:
|
|
(37) |
Зависимость от температуры задается уравнением:
|
|
(38) |
Знание величин изменений стандартной энергии Гиббса и энтальпии позволяет вычислить равновесный состав смеси и определить его функцию от температуры.



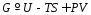



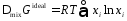




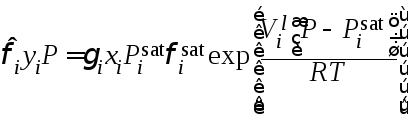
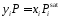
 BB→
BB→ jJ+
jJ+ kK+…
kK+…