
- •Н.В. Лисицын
- •Содержание
- •1 Ресурсы и ресурсосберегающие технологии
- •1.1 Устойчивое развитие, жизненный цикл
- •1.2 Критерии оценки больших систем
- •1.3 Ресурсосбережение
- •2 Основные термодинамические приложения для анализа химико-технологических систем
- •2.1 Энтропия и ее производство
- •2.2 Первый и второй законы термодинамики. Производство энтропии.
- •2.3 Изменение состава систем. Энтропия процессов смешения и химического превращения
- •2.4 Коэффициент полезного действия систем
- •3 Эффективность карно и потери полезной работы систем
- •3.1 Потребление полезной работы
- •3.2 Уравнение Гюи – Стодолы
- •3.3 Задача производства энтропии в общем виде
- •4. Причины и следствия увеличения энтропии систем
- •4.1 Движущие силы и потоки
- •4.2 Феноменологические законы
- •4.3 Принцип симметрии кинетических коэффициентов
- •4.4 Ограниченность применения линейных законов тепло – и массопереноса
- •5. Энергетические потери и неравновесность
- •5.1 Внутренне обратимый двигатель Карно
- •5.2 Принцип равномерного распределения энергии
- •5.3 Прямоточный и противоточный процессы теплообмена
- •6 Эксергия и эксергетический баланс процесса
- •6.1 Эксергия, энергия Гиббса и полезность
- •6.2 Эксергетический баланс
- •6.3 Физическая эксергия. Эксергия смешения
- •6.4 Качество источников энергии
- •7. Физическая и химическая эксергия
- •7.1 Эксергия компонентов воздуха
- •7.2 Химическая эксергия соединений
- •7.3 Энергия Гиббса образования и химическая эксергия
- •8 Эксергетический и энергетический анализ и балансы
- •8.1 Основные недостатки энергетического анализа систем
- •8.2 Уравнения баланса массы, энергии, эксергии и энтропии
- •9 Анализ процессов производства электроэнергии
- •9.1 Основные процессы производства энергии
- •9.2 Сжигание угля и газа
- •9.3 Термодинамическая эффективность газового цикла
- •9.4 Эффективности парового цикла
- •9.5 Эффективность объединенного цикла
- •10 Анализ процессов разделения
- •10.1 Однократная равновесная перегонка бинарной смеси
- •10.2 Термодинамический анализ идеальной дистилляционной колонны
- •10.3 Анализ реальной колонны
- •11 Анализ химико-технологических систем. Основные правила ресурсосбережения
- •11.1 Процедура анализа систем
- •11.2 Эвристические правила экономии материальных и энергетических ресурсов
- •4. Если химическая реакция протекает с выделением тепла, необходимо ее начинать при повышенной (не при пониженной) температуре (рис.49).
- •12 Методические рекомендации по выполнению контрольных работ
- •13 Контрольные работы
- •13.1 Контрольная работа №1
- •13.2 Контрольная работа №2
- •13.3 Контрольная работа №3
- •Кафедра ресурсосберегающих технологий
- •Теоретические основы энерго- и ресурсосбережения
- •190013, Санкт-Петербург, Московский пр., 26
7. Физическая и химическая эксергия
7.1 Эксергия компонентов воздуха
Как
было отмечено ранее, эксергия выражает
максимум полезной работы или потенциальную
возможность совершения работы в связи
с разницей в давлении, температуре и
составе по сравнению с окружающей
средой. Физическая эксергия,
 учитывает различия в давлении и
температуре; стандартная химическая
эксергия
учитывает различия в давлении и
температуре; стандартная химическая
эксергия – в составе по сравнению с окружающей
средой при давлении и температуре
окружающей среды.
– в составе по сравнению с окружающей
средой при давлении и температуре
окружающей среды.
|
|
|
Удобство понятия эксергии дает возможность обсуждать вопросы, касающиеся энергии, на четкой количественной основе, особенно если величина эксергии, определенная для потоков, участвующих в процессе, объединяется с потерями эксергии, происходящими в ходе процесса, в котором участвует поток, активно или пассивно.
Величина эксергии зависит от того, до какой степени вещество или смесь далеки от состояния равновесия с окружающей средой. Разность температур приводит к переносу теплоты, в то время как разность давлений приводит к переносу вещества. Физическая эксергия представляет собой наибольшую работу, которую может совершить система при приведении давления и температуры системы к давлению и температуре окружающей среды.
Обнаруживается, однако, что, если физическая эксергия равна нулю и, значит, система находится в состоянии равновесия с окружающей средой, она может, тем не менее, существовать вне его по другим параметрам. Сущность этого явления лежит в разнице состава и природы компонентов, образующих систему и окружающую среду, которое может быть описано эксергией смешения и химической эксергией.
Чтобы
прояснить понятие эксергии смешения,
приведем пример чистого кислорода при
произвольных условиях
 и
и .
Рассмотрим систему, для удобства
выбранную при
.
Рассмотрим систему, для удобства
выбранную при и
и ,
изолированную от окружающей среды и
состоящую из двух отдельных частей,
содержащих кислород и воздух,
соответственно. Пусть эти две части,
первоначально разделенные мембраной,
и, следовательно, находящиеся в
механическом и термическом равновесии,
при ее удалении приводятся в контакт
друг с другом. Кислород и воздух будут
взаимно диффундировать, и равновесие
будет достигнуто, когда кислород и
воздух образуют гомогенную смесь.
,
изолированную от окружающей среды и
состоящую из двух отдельных частей,
содержащих кислород и воздух,
соответственно. Пусть эти две части,
первоначально разделенные мембраной,
и, следовательно, находящиеся в
механическом и термическом равновесии,
при ее удалении приводятся в контакт
друг с другом. Кислород и воздух будут
взаимно диффундировать, и равновесие
будет достигнуто, когда кислород и
воздух образуют гомогенную смесь.
Первоначально
кислород не находится в состоянии
полного равновесия с окружающей средой
(т.е. с воздухом), несмотря на равенство
давлений ( )
и температур (
)
и температур (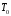 ).
Термодинамический потенциал чистого
кислорода выше термодинамического
потенциала кислорода в воздухе при
).
Термодинамический потенциал чистого
кислорода выше термодинамического
потенциала кислорода в воздухе при и
и .
При смешении компонентов воздуха, взятых
в виде чистых веществ, до однородной
смеси термодинамический потенциал
каждого из них уменьшается. Изменение
эксергии системы будет равно:
.
При смешении компонентов воздуха, взятых
в виде чистых веществ, до однородной
смеси термодинамический потенциал
каждого из них уменьшается. Изменение
эксергии системы будет равно:
|
|
(1) |
Так
как процесс смешения протекает при
 и
и ,
можно записать:
,
можно записать:
|
|
(2) |
Величина эксергии смешения при параметрах смеси Р, Т и заданном составе, в соответствии со значениями эксергии чистых компонентов при Р и Т, будет равна:
|
|
(3) |
где
для расчета
 значения
значения и
и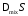 беруться при условияхР
и Т.
беруться при условияхР
и Т.
Чтобы
найти значения химической эксергии
веществ, нужно определить для них
сравнительную точку отсчета –
окружающую
среду, которая соответствует природной
среде и
состоит из компонентов атмосферы,
океанов и земной коры. В природе
(атмосфере, океанах и в верхнем слое
земной коры) находятся вещества при
параметрах
 и
и .
Они могут взаимодействовать друг с
другом с образованием стабильного
состояния, и поэтому энергия Гиббса
системы, образованной этими веществами,
будет стремиться к минимальной величине.
Следовательно, значение энергии Гиббса
системы «сравнительная окружающая
среда» – на уровне моря в состоянии
покоя при отсутствии иных силовых полей,
кроме гравитационного – можно определить
как нулевое значение и принять величину
термодинамического потенциала для
каждого из веществ равным нулю (0 Дж/моль).
.
Они могут взаимодействовать друг с
другом с образованием стабильного
состояния, и поэтому энергия Гиббса
системы, образованной этими веществами,
будет стремиться к минимальной величине.
Следовательно, значение энергии Гиббса
системы «сравнительная окружающая
среда» – на уровне моря в состоянии
покоя при отсутствии иных силовых полей,
кроме гравитационного – можно определить
как нулевое значение и принять величину
термодинамического потенциала для
каждого из веществ равным нулю (0 Дж/моль).
По отношению к «сравнительной окружающей среде» могут быть определены термодинамические потенциалы всех веществ при параметрах, отличных от нулевого состояния, т.е. при Р и Т.
«Сравнительная
окружающая среда» не может совершать
какой бы то ни было работы, поэтому ее
состояние может считаться базовым для
значений эксергии при
 и
и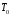 ,
которые по определению будут равны
химическим потенциалам веществ
(подсистем) на уровне моря, в состоянии
покоя и при отсутствии любых полей,
кроме гравитационного:
,
которые по определению будут равны
химическим потенциалам веществ
(подсистем) на уровне моря, в состоянии
покоя и при отсутствии любых полей,
кроме гравитационного:

Проиллюстрируем понятие «сравнительной окружающей среды» на конкретных примерах.
Сравнительные компоненты.
Как
было показано, различие в термодинамических
потенциалах кислорода и воздуха является
причиной отсутствия равновесия с
окружающей средой при нулевых параметрах ,
, и это далеко не единственный случай.
Рассмотрим графит. Графит самопроизвольно
реагирует с кислородом с образованием
диоксида углерода, но по кинетическим
закономерностям реакция протекает
крайне медленно и графит кажется
стабильным в окружающей среде, хотя на
самом деле в присутствии кислорода его
состояние метастабильно, что как раз
обусловлено возможностью образования
диоксида углерода. В результате фактически
мы имеем значительное количество
доступной химической эксергии, и графит
может рассматриваться как важный
энергоноситель, так как потенциально
он находится далеко за пределами
равновесия с окружающей средой.
и это далеко не единственный случай.
Рассмотрим графит. Графит самопроизвольно
реагирует с кислородом с образованием
диоксида углерода, но по кинетическим
закономерностям реакция протекает
крайне медленно и графит кажется
стабильным в окружающей среде, хотя на
самом деле в присутствии кислорода его
состояние метастабильно, что как раз
обусловлено возможностью образования
диоксида углерода. В результате фактически
мы имеем значительное количество
доступной химической эксергии, и графит
может рассматриваться как важный
энергоноситель, так как потенциально
он находится далеко за пределами
равновесия с окружающей средой.
В
окружающей среде существует множество
соединений подобных кислороду, которые
не могут диффундировать или претерпевать
химические преобразования до более
стабильных состояний и могут в связи с
этим считаться находящимися в состоянии
равновесия. Ни химические, ни ядерные
реакции не могут перевести эти компоненты
в более стабильные соединения. Эти
вещества не могут совершать никакую
полезную работу, и, следовательно, их
эксергия считается равной нулю. К ним
принадлежат:
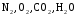 и
и при
при =298,15 К и
=298,15 К и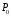 = 99,31 кПа (среднее атмосферное давление).
Их парциальные давления
= 99,31 кПа (среднее атмосферное давление).
Их парциальные давления в воздухе приведены в таблице 4.
в воздухе приведены в таблице 4.
Из
этих данных можно рассчитать величины
химической эксергии компонентов в
чистом
состоянии
при
 и
и .
Воздух в этих условиях может рассматриваться
в качестве идеального газа, следовательно,
разделение его составляющих будет
протекать без теплового эффекта:
.
Воздух в этих условиях может рассматриваться
в качестве идеального газа, следовательно,
разделение его составляющих будет
протекать без теплового эффекта: .
Единственным фактором, влияющим на
формирование эксергии разделения
.
Единственным фактором, влияющим на
формирование эксергии разделения (см. уравнение (3)), будет энтропия
разделения:
(см. уравнение (3)), будет энтропия
разделения:
|
|
(4) |
Таблица 4 - Парциальные давления веществ воздуха
|
Компонент |
|
Компонент |
|
|
|
75,78 |
|
0,000485 |
|
|
20,39 |
|
0,00177 |
|
|
0,0335 |
|
0,906 |
|
|
2,2 |
|
0,000097 |
|
|
0,000342 |
|
0,0000087 |
Изменение
энтропии, связанное с переводом одного
моля идеального
газа изотермически от давления
 к давлению
к давлению задается уравнением:
задается уравнением:
|
|
(5) |
из
которого следует, что стандартная
химическая эксергия при
 и
и для чистого вещества может быть вычислена
на основании его парциального давления
в воздухе :
для чистого вещества может быть вычислена
на основании его парциального давления
в воздухе :
|
|
(6) |
Значения
эксергии для элементов в их стабильном
состоянии при
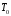 =
298,15К и
=
298,15К и =101,325 кПа называются их стандартнойхимической
эксергией. Стандартные величины
химической эксергии основных компонентов
воздуха приведены в таблице 5.
=101,325 кПа называются их стандартнойхимической
эксергией. Стандартные величины
химической эксергии основных компонентов
воздуха приведены в таблице 5.
Таблица
5 - Значения стандартной химической
эксергии при
 и
и для различных компонентов воздуха
для различных компонентов воздуха
|
Компонент |
|
Компонент |
|
|
|
0,72 |
|
30,37 |
|
|
3,97 |
|
27,19 |
|
|
19,87 |
|
11,69 |
|
|
9,49 |
|
34,36 |
|
|
31,23 |
|
40,33 |
Пример для графита показывает, каким образом можно вычислить значение химической эксергии веществ.
Графит
реагирует с кислородом с образования
 при
при и
и согласно
формулы:
согласно
формулы:
|
|
(7) |
в
которой участвуют соответствующие
значения стандартной энергии Гиббса
образования веществ
 :
:
|
|
(8) |
где
 – стехиометрический коэффициент,
положительный для продуктов реакции и
отрицательные для реагентов, а
– стехиометрический коэффициент,
положительный для продуктов реакции и
отрицательные для реагентов, а – стандартный термодинамический
потенциал или энергия Гиббса для вещества
i.
Уравнение (8) основано на образовании 1
моля рассматриваемого соединения, в
нашем случае – это 1 моль
– стандартный термодинамический
потенциал или энергия Гиббса для вещества
i.
Уравнение (8) основано на образовании 1
моля рассматриваемого соединения, в
нашем случае – это 1 моль
 .
.
Изменение эксергии будет равно:
|
|
(9) |
Тогда эксергия графита может быть вычислена так:
|
|
(10) |
Значения
стандартных энергий Гиббса образования
веществ
 для соединений приведены в справочниках
термодинамических величин. Величина
для соединений приведены в справочниках
термодинамических величин. Величина
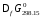 для
для составляет – 394,359 кДж/моль. На основании
данных таблицы 5, будем иметь
составляет – 394,359 кДж/моль. На основании
данных таблицы 5, будем иметь
 =
394,359 +19,87 – 3,97=410,26 кДж/моль.
=
394,359 +19,87 – 3,97=410,26 кДж/моль.
Для остальных элементов в качестве сравнительных соединений были выбраны те вещества, в виде которых элементы существуют в морской воде, литосфере или земной коре. Важный аспект этого выбора состоит в том, что рассчитанные значения эксергии для всех веществ должны быть положительны. В таблице 6 приведены значения стандартной химической эксергии элементов.
Таблица 6 - Значения стандартной химической эксергии элементов
|
Элемент |
|
Элемент |
|
|
Ag(s) |
70.2 |
Kr(g) |
34.36 |
|
Al(s) |
888.4 |
Li(s) |
393.0 |
|
Ar(s) |
11.69 |
Mg(s) |
633.8 |
|
As(s) |
494.6 |
Mn(sα) |
482.3 |
|
Au(s) |
15.4 |
Mo(s) |
730.3 |
|
B(s) |
628.5 |
N2(g) |
0.72 |
|
Ba(s) |
747.7 |
Na(s) |
336.6 |
|
Bi(s) |
274.5 |
Ne(g) |
27.19 |
|
Br2(l) |
101.2 |
Ni(s) |
232.7 |
|
C(s, графит) |
410.26 |
O2(g) |
3.97 |
|
Ca(s) |
712.4 |
P(s, красный) |
863.6 |
|
Cd(sα) |
293.2 |
Pb(s) |
232.8 |
|
Cl2(g) |
123.6 |
Rb(s) |
388.6 |
|
Co(sα) |
265.0 |
S(s,ромбическая) |
609.6 |
|
Cr(s) |
544.3 |
Sb(s) |
435.8 |
|
Cs(s) |
404.4 |
Se(s,черный) |
346.5 |
|
Cu(s) |
134.2 |
Si(s) |
854.6 |
|
D2(g) |
263.8 |
Sn(s, белый) |
544.8 |
|
F2(g) |
466.3 |
Sn(s) |
730.2 |
|
Fe(sα) |
376.4 |
Ti(s) |
906.9 |
|
H2(g) |
236.1 |
U(s) |
1190.7 |
|
He(g) |
30.37 |
V(s) |
721.1 |
|
Hg(l) |
115.9 |
W(s) |
827.5 |
s – твердый, l – жидкий, g – газообразный





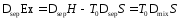
 ,
кПа
,
кПа ,
кПа
,
кПа

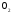
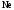
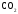
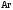

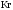
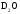
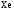


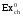 ,
кДж/моль
,
кДж/моль ,
кДж/моль
,
кДж/моль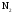


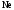

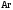
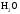

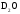





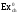 ,
(кДж/моль)
,
(кДж/моль) ,
(кДж/моль)
,
(кДж/моль)