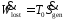5. Энергетические потери и неравновесность

5.1 Внутренне обратимый двигатель Карно

Согласно второму закону в ходе проведения реальных процессах (а, следовательно, и в инженерной практике) всегда соблюдается неравенство:

При этом существуют потери, равные:	(1)
	(2)

Производство энтропии связано со скоростями потоков в процессе, такими как объемная скорость потока вещества V, массовая (в молях), скорость реакции, поток теплотыи т.д., и вызвавшими их силами ∆(Р/Т), –∆(μ/Т), А/Т, ∆(1/Т). Скорость производства энтропии равна:

(3)

Исключая из уравнений (2) и (3), получим:

(4)

откуда следует, что потери, обусловленные неравновесностью процесса, также напрямую связаны со скоростями потоков, присутствующих в процессе, и с движущими силами, а доступная работа (эксергия) всегда рассеивается.

При стремлении к нулю движущих сил энергетические потери, также будут приближаться к нулю. Но это состояние нереалистично, так как с этом случае потоки также будут стремиться к нулю. На практике инженер имеет дело с оборудованием конечного размера, которое работает в течение конечного времени. Вопрос заключается в том, при такихограничениях достигается наименьшее количество энергетических потерь, связанных с неравновесностью. Очевидно, что минимизация энергетических потерь и, следовательно, производства энтропии – сложная оптимизационная задача с множеством аспектов. Рассмотрим ее решение на примере теплообменника. Ранее было установлено, что наибольшее количество доступной работы потока теплоты при постоянной температуре равно величине:

(5)

которая может быть получена при работе теплового двигателя Карно, и конкретно между температурами и(рис. 18).

Рисунок 18 - Двигатель Карно, работающий между температурами и

Теплота изотермически передается от источника, имеющего температуру 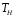к рабочей жидкости, в то время как количество теплоты, равноепередается от рабочей жидкости к окружающей среде ().

Однако известно, что в действительности не существует такого явления как изотермический перенос теплоты.

В соответствии с уравнением

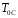перенос конечного количества теплоты требует конечной разности температур ∆Т, или более корректно, ∆(1/Т). Поэтому можно предположить, что рабочая жидкость, строго говоря, функционирует в другом диапазоне температур, между и, а не междуи(рис.19), что, безусловно, подразумевает потерю мощности обусловленную энергетическими потерями в интервалах температури, а такжеи. Величина потерь равна:

(6)

Рисунок 19 - Внутренне обратимый двигатель Карно, работающий между

температурам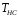и и

Чем больше значения тепловых потоков и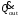, тем выше необходимые и связанные с ними разности температур для переноса теплоты к рабочей жидкости (при высоких температурах) и от рабочей жидкости (при низких температурах) для теплообменников, а, следовательно, и обусловленные ими потери. Если сделать допущение, что эти потери в ходе теплопереноса являются единственными, то двигатель Карно можно продолжать считать обратимым, точнее внутренне обратимым, подразумевая, что сам цикл Карно не вызывает потерь.

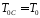Анализ внутренне обратимого двигателя свидетельствует о наличии двух граничных положений. Первое, когда и, (точка 1 на рис.20), т.е. когда теплота бесконечно медленно обратимо исходит от источника тепла и передается двигателю. Эффективность двигателя равна эффективности двигателя Карно, работающего междуи:, посколькуи, что является граничным случаем. Второе положение соответствует точке 2, в которой скорость перемещения теплоты внутри цикла достигает максимума и вся доступная работа рассеивается между температурамиииипри условии, что. Работа, изначально доступная в виде потока теплоты, управляющего двигателем, проходит сквозь двигатель в окружающую среду при температуре, тогда как в первом случае вся доступная работа, уходила в окружающую среду не попадая в двигатель.

Рисунок 20 - Зависимость мощности 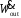и эффективности работыη внутренне обратимого двигателя Карно от скорости потока теплоты

Очевидно, что в промежуточном положении между точками 1 и 2 двигатель может работать с различной эффективностью. Но должна существовать точка, при которой скорость подвода теплоты будет оптимальной и итоговая мощность двигателя достигнет максимума (точка 3 на рис.20). Это положение соответствует двум оптимальным температурам и, связанным с температурамиивыражением:

(7)

а соответствующая термодинамическая эффективность будет равна:

(8)

Существование оптимальных температур покажем с помощью следующего рассуждения. Предположим, что нужно ввести теплоту в цикл Карно со постоянной скоростью . Условие постоянство скорости входного потока теплоты позволит тем самым «зафиксировать» верхнюю температуруцикла Карно, поскольку они связаны выражением:

(9)

при условии постоянства k и А – общего коэффициента и площади теплопередачи. Постоянное значение , в свою очередь, позволит зафиксировать нижнюю температуру. Зависимость, связывающая между собой полученную и отданную теплоту, имеет вид:

(10)

или:

(11)

Мощность двигателя задается выражением:

(12)

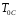Варьируя между двумя крайними точками 1 и 2 можно получить оптимальную величину, для которой значениемаксимально, как показано на рис. 20. Максимальная мощность соответствует оптимальным значениям температур, между которыми работает двигатель Карно,и. Оптимальные температуры связаны с, температурой, при которой теплота становится полезной, и– температурой, которая выступает в роли «поглотителя» для теплоты, выдаваемой двигателем. Максимизируя значениес учетом, получаем уравнения (7) и (8).

Может создаться ощущение, что работа с максимальной мощностью не может происходить при наиболее благоприятных условиях, а именно – при минимальной скорости производства энтропии. Однако это возможно, если условия максимальной мощности являются условиями наименьшей скорости производства энтропии, точно совпадающими с теми, которых можно ожидать, исходя из соотношения Гюи-Стодолы. По существу, необходимо определить совокупный вклад в скорость производства энтропии последовательно для каждого из трех диапазонов температур.

Первый вклад обусловлен теплообменом на более горячем конце двигателя Карно:

(13)

Второй вклад вносит теплообмен на более холодном конце двигателя:

(14)

Третий вносит исходный поток теплоты после того, как он передал часть тепладвигателю. Предположим, что этим потокомявляется насыщенный пар, конденсирующийся придо степени, которая зависит от теплоты, переданной двигателю. Покинув теплообменник, поток теплотыобменивается теплом с окружающей средой при температуре, что приводит к определению значения третьей составляющей:

Общее производство энтропии будет равно:

(15)

Минимизируя с учетом ивеличину, можно, как и в предыдущем случае, получить оптимальные значения для,ии величину наибольшей мощности (рис.21).

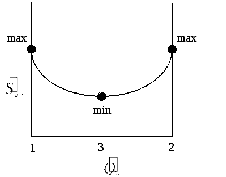
Рисунок 21 - Скорость производства энтропии как функция потока теплоты

В точке 1 двигатель работает так медленно, что вся полезная работа входного потока рассеивается вне двигателя: иравны нулю, а значениедостигает максимальной величины. В точке 2 прився полезная работа вновь рассеивается, а скорость производства энтропии максимальна. И в точке 1, и в точке 2 теплота, изначально доступная при температуре, передается окружающей среде, что обуславливает наибольшее производство энтропии.

Оптимальный поток теплоты расположен между нулевым и максимальным значением. При нулевом потоке двигатель работает с максимальной эффективностью, равной эффективности по Карно, но он не совершает работы по причине бесконечно малой скорости. Вся полезная работа рассеивается в окружающую среду. При максимальной скоростивыход тоже равен нулю, так как вся полезная работа протекаетсквозь систему за ее пределы. Для оптимальной скорости, расположенной между крайними значениями, итоговая мощность максимальна и наблюдается минимальное рассеивание работы и соответственно минимальное производство энтропии.

Анализ энергетических потерь, связанных с неравновесностью процесса приводит к следующим рассуждениям.

Существует источник теплоты, доступной при температуре при постоянной скорости ее поступления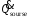, что фиксирует количество доступной работы, которая может быть выполнена, исходя из ресурсов источника в единицу времени. Наибольшая доля этой работы, которая может быть получена в качестве максимальной итоговой мощности системы,реализуется для оптимального значения величины– скорости, при которой теплота переносится от источника к внутренне обратимому циклу Карно. Остальная часть,, уходит в окружающую среду и равна. Если, например,– мощность электростанции, то это означает, что данное конечное количество работы должно быть произведено законечное время. Величина оптимального значения теплоты , соответствующаяопределяется с помощью выражения:

и является также конечной.

Оптимальное значение верхней температуры двигателя Карно, 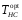, получается как результат решения приведенного соотношения и зависит от общего коэффициента теплопереносаk и конечного размера теплообменника, а именно – от площади поверхности теплообмена. Выбор других материалов, из которых может быть изготовлен теплообменник будет, несомненно, влиять на результат.

Термодинамика конечного пространства и конечного времени играет важную роль. Идеализированные ограничения Карно или ограничения обратимого цикла заменяются на более реалистичные представления о действительных процессах, что достигается с помощью комбинирования результатов равновесной термодинамики и тех результатов неравновесной термодинамики, которые в большей степени согласуются со скоростями и движущими силами процессов.