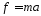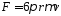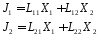4.2 Феноменологические законы

Хотя необратимая термодинамика четко определяет движущие силы, отвечающие соответствующим потокам, она ничего не говорит о соотношениях между этими двумя величинами. Подобные соотношения были получены из эксперимента и известны как эмпирические феноменологические законы: Фурье – для теплопроводности, Фика – для простой бинарной диффузии вещества и Ома – для электропроводности. Эти законы представляют собой линейные соотношения между силой и соответствующим потоком, что верно в положении, близком к состоянию равновесия. Формально они могут быть записаны следующим образом:

Закон теплопроводности Фурье:

Закон диффузии Фика:

Закон электропроводности Ома: (а)

Другая форма закона Ома: (б)

где к – коэффициент (константа) теплопроводности, – коэффициент диффузии компонентаk и – концентрация компонентаk.

Закон Ома обычно представляют в форме (а), где I – сила тока, R – сопротивление и V – напряжение, но существует другая форма записи через плотность электрического тока I, электрическое поле Е и удельное сопротивление 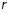(сопротивление на единицу длины и единицу площади поперечного сечения).

Константы теплопроводности, диффузии и электропроводности (обратная величина сопротивления), представляют собой хорошо известные коэффициенты пропорциональности, связывающие движущие силы и соответствующие потоки обратная величина сопротивления:

(8)

Обобщенное название всех этих констант – феноменологические коэффициенты ().

Закон Ньютона представляет собой особый случай. Он связывает силу с ускорением:

(9)

Это соотношение выведено, однако, для среды, в которой отсутствует трение. Если силы трения учитываются, ускорение уменьшается, а строгое линейное соотношение между скоростью v и силой f может быть установлено в виде закона Стокса, который четко подпадает под вышеупомянутую категорию. Закон Стокса гласит, что сила сопротивления (трения), испытываемая твёрдым шаром при его медленном поступательном движении в неограниченной вязкой жидкости пропорциональна радиусу шара, скорости движения шара и коэффициенту вязкости жидкости:

где F – сила, r – радиус, – коэффициент вязкости жидкости,v – скорость.

Уравнение (8) может быть представлено в виде:

(10)

В этом уравнении, также как в адаптированном для присутствия сил трения законе Ньютона, выведена обратная величина феноменологического коэффициента , которая рассматривается в качестве коэффициента трения, сопротивления.

Объединяя соотношения

(11)

и

(12)

приходим к зависимости между работой, потерянной в ходе процесса, и имеющимися силами трения:

(13)

Это уравнение отражает физический смысл явлений, происходящих в природе: в процессах с различными потоками 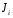работа непрерывно рассеивается на преодоление барьеров, сопротивления или трения, которые подразумевают под собой все процессы тепло – или массопереноса и химического превращения.

4.3 Принцип симметрии кинетических коэффициентов

Ранее обсуждалось соотношение между одной движущей силой и взаимосвязанным с ней (взаимным, сопряженным) потоком. Эмпирически установлено большое количество пропорциональных зависимостей между потоками и силами. Но эксперименты свидетельствовали и о возможных отклонений от прямолинейности таких связей. Так, например, скорость потока могла быть линейно связана с движущей силой, а скорость потока– с движущей силойи т.д. Подобные наблюдения были получены при изучении взаимодействия электрического и осмотического поведения, для потоков вещества и теплоты, потоков электричества и теплоты. Попытка объяснить указанные явления привела норвежского ученого Ларса Онзагера, инженера-химика и лауреата Нобелевской премии, к открытию принципа симметрии кинетических коэффициентов, послужившего основой феноменологической термодинамики неравновесных процессов и составлению так называемых феноменологических уравнений:

(14)

или

(15)

Альтернативная формулировка может быть дана в соответствии с выражением

(16)

где коэффициенты представляют собой обобщенные сопротивления или силы трения.

Коэффициенты и– называются, как указывалось ранее, феноменологическими или, по Онзагеру, кинетическими коэффициентами, для которых справедливо равенство:

(17)

или

(18)

Приближенное описание процесса с помощью представленных линейных соотношений справедливо только в случае его чрезвычайно медленного протекания и термодинамического состояния вблизи равновесного. Но даже тогда не все потоки могут быть взаимосвязанными, так как взаимность ограничивается определенными случаями.

Теперь следует выяснить, как этот принцип влияет на величины и. Согласно выражению (12):

(19)

Рассмотрим для наглядности случай двух пар линейно связанных потоков и сил. Тогда:

(20)

и

(21)

Требование второго закона, выраженное неравенством 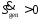, приводит к необходимости выполнения условий:

(22)

и

(23)

Следует заметить, что здесь конкретно не указывается знак . Для тройных смесей, где два растворенных вещества диффундируют в среде растворителя, известны случаи отрицательных коэффициентов, а наличие симметрии может приводить к 25%-ному уменьшению скорости производства энтропии. Известны случаи, когда наблюдалось движение вещества в направлении, противоположном градиенту термодинамического потенциала, что вызывало отрицательный вклад в значение.