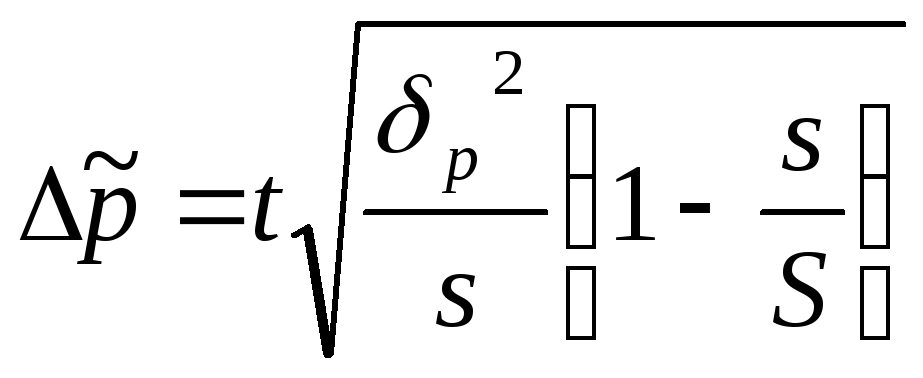Приклади

Приклад 1. Методом випадкової вибірки було взято для перевірки ваги 200 шт. деталей. В результаті було встановлено, що середня вага деталі 30г, при середньоквадратичному відхиленні 4г.

З ймовірністю 0,954 потрібно визначити границі, в яких знаходиться середня вага деталі в генеральній сукупності.

За умовою задачі:

= 30г.

n = 200

σ = 4г.

Р = 0,954

t = 2,0

Згідно з формулою 7.9 середня вага деталі в генеральній сукупності буде знаходитися в межах:

.

Для визначення меж потрібно в першу чергу розрахувати :

звідси:

,

тобто з ймовірністю 0,954 можна стверджувати, що середня вага однієї деталі в генеральній сукупності буде знаходитися в межах 29,44 – 30,56.

Приклад 2. При дослідженні 100 зразків виробів, відібраних із партії у випадковому порядку, 20 виявились нестандартними. З ймовірністю 0,954 визначити межі, в яких знаходиться частка нестандартної продукції в генеральній сукупності.

За умовою задачі:

n = 100

m = 20

Р = 0,954

t = 2,0

Згідно з формулою 7.10 частка нестандартної продукції у генеральній сукупності буде знаходитися в межах:

.

Частка нестандартної продукції у вибірці становить:

.

Гранична помилка частки дорівнює:

.

Частка нестандартної продукції в генеральній сукупності буде знаходитися в межах:

тобто з ймовірністю 0,954 частка нестандартної продукції в генеральній сукупності буде знаходитися в межах 0,12 - 0,28.

Для серійної вибірки узагальнюючі характеристики визначаються за такими формулами:

середня

–повторна вибірка, (7.11)

–безповторна вибірка, (7.12)

частка

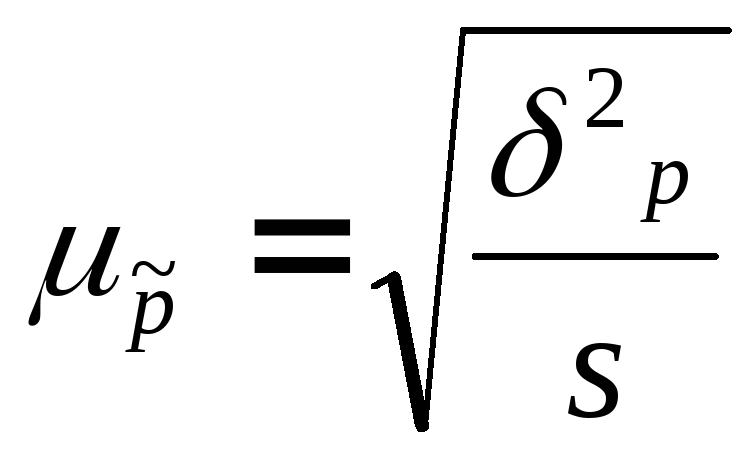–повторна вибірка, (7.13)

–безповторна вибірка, (7.14)

де – міжсерійна дисперсія;

s – число відібраних серій;

S – загальне число серій в генеральній сукупності;

–міжсерійна (міжгрупова) дисперсія частки, яка визначається за формулою:

,

де р_і – частка ознаки в і-й серії;

–частка ознаки для всієї серії.

Середня гранична помилка для серійної вибірки визначається як добуток середньої помилки вибірки (формули 7.11, 7.12, 7.13, 7.14) на коефіцієнт довіри t.

В таблиці 7.2 наведені середні граничні помилки для серійної вибірки.

Таблиця 7.2 - Середні граничні помилки для серійної вибірки

Узагальнювальні характеристики	Схема відбору
	повторна	безповторна
Середня
Частка

Визначення меж, в яких знаходиться середня в серійних вибірках, розглянемо на прикладі.

Із сукупності, що розбита на 100 рівних по величині серій, методом механічного відбору відібрано 10 серій. Міжсерійна дисперсія дорівнює 20, а середня величина ознаки у вибірці – 140. З ймовірністю 0,997 визначити межі, в яких знаходиться середня в генеральній сукупності:

За умовою задачі:

S = 100

s = 10

δ² = 20

Р = 0,997

t = 3,0

Середня находиться в межах:

.

Середня гранична помилка для серійної вибірки:

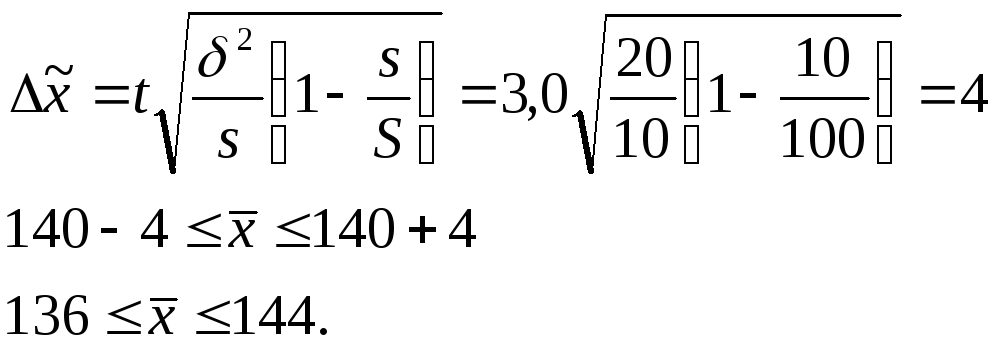
Отже, середня величина ознаки в генеральній сукупності з ймовірністю 0,997 буде в межах 136-144 одиниць.