7.3 Середня і гранична помилки вибірки
Досягнути точного збігу узагальнюючих показників вибіркової і генеральної сукупності практично неможливо. Таке завдання і не ставиться в процесі досліджень. Мова може іти тільки про максимальне наближення показників вибіркової сукупності до показників генеральної сукупності, визначення можливої границі відхилення цих показників і умов, від яких залежить величина цих відхилень.
Можливі границі відхилень вибіркової частки і вибіркової середньої від частки і середньої в генеральній сукупності носять назву помилки вибірки.
У кожній окремій вибірці відхилення між узагальнюючими показниками у вибірковій і генеральній сукупності приймають різні значення. Тому мова може іти тільки про середню помилку вибірки.
Чим більша чисельність вибіркової сукупності, тим при інших рівних умовах, менша середня величина помилки вибірки.
При однаковій чисельності вибіркової сукупності середня помилка вибірки буде менша в тій сукупності, яка відібрана із генеральної сукупності з меншою мінливістю досліджуваної ознаки.
Звідси, помилка вибірки для середньої визначається за формулою:
,
(7.1)
де
– середня помилка вибірки для середньої;
–дисперсія
варіюючої ознаки;
n – чисельність одиниць вибіркової ознаки.
Середня помилка для частки дорівнює:
,
(7.2)
,
(7.3)
де
– середня помилка вибірки для частки;
р – вибіркова частка ознак, що досліджуються;
m – число одиниць у вибірковій сукупності, яким притаманні ознаки, що досліджуються;
n – число одиниць вибіркової сукупності.
Наприклад, якщо у відібраній партії із 100 деталей 5 виявилось бракованими, то n = 100, m = 5, р = 5:100=0,05.
Чисельник формули 7.2 є дисперсією для альтернативної ознаки (частки), що доводиться таким чином.
Ознаки, які мають одні одиниці сукупності, а інші не мають, називаються альтернативними.
Частка одиниць, які мають ознаку в чисельності всієї сукупності, позначають через р, а частка одиниць, що не мають цієї ознаки – через q.
Звідси:
p + q = 1, a q = 1 – p.
Варіація альтернативної ознаки дорівнює нулю у одиниць, які не мають цієї ознаки. Звідси:
.
(7.4)
Дисперсія альтернативної ознаки дорівнює:
,
(7.5)
що і потрібно було довести.
Формули 7.1 і 7.2 відносяться до повторної вибірки. Для безповторної вибірки зазначені формули мають такий вигляд:
для
середньої
,
(7.6)
для
частки
.
(7.7)
Наведені формули середньої помилки характеризують тільки середнє відхилення узагальнюючих характеристик.
Однак стверджувати, що генеральна середня не вийде за певні границі, можна не з абсолютною достовірністю, а лише з певним ступенем ймовірності.
Для того, щоб визначити границі, в яких знаходиться середнє значення і частка в генеральній сукупності, визначається гранична помилка вибірки.
Між середньою і граничною помилкою вибірки існує таке співвідношення:
= t , (7.8)
де - гранична помилка вибірки;
- середня помилка вибірки;
t – коефіцієнт довіри, який визначається в залежності від рівня ймовірності (Р):
для Р = 0,683 t = 1,0,
для Р = 0,954 t = 2,0,
для Р = 0,997 t = 3,0.
В таблиці 7.1 наведені формули для визначення граничної помилки вибірки на основі узагальнювальної формули 7.8.
Таблиця 7.1 - Граничні помилки вибірки
-
Узагальнювальні
характеристики
Схема відбору
повторна
безповторна
Середня
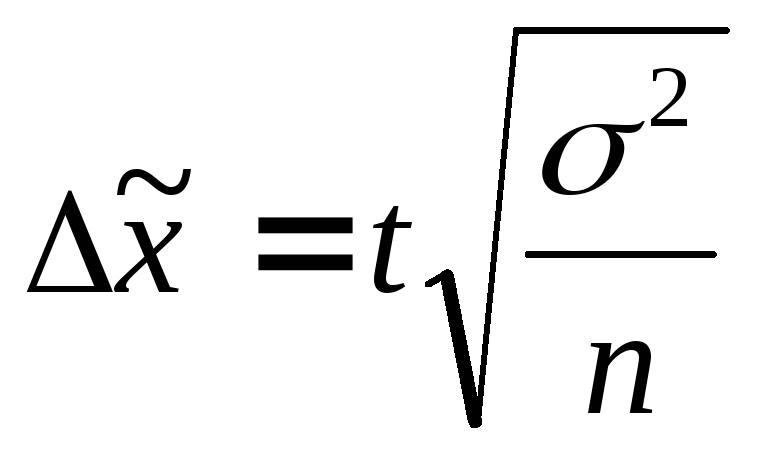
Частка
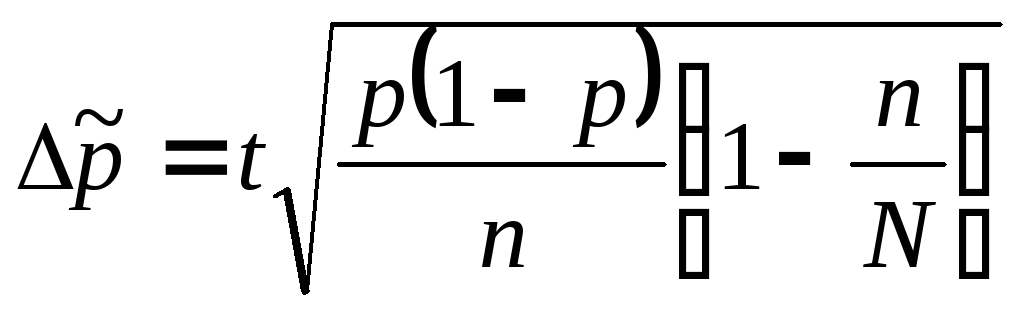
На підставі граничних помилок визначаються граничні значення
середньої і частки в генеральній сукупності:
–для
середньої величини, (7.9)
–для
частки. (7.10)