Параметри рівняння розрахуємо за формулами 9.4:

а₀=;

а₁=.

Таким чином , рівняння, яке описує зв’язок між вартістю основних фондів та обсягом товарної продукції, має такий вигляд:

у=13,8+5,6х

Розрахункове значення функції одержане шляхом послідовного використання фактичного значення фактора (х) в побудованому рівнянні:

=і т.д.

Про вірність розрахунків параметрів рівняння (а_0,а_і ) свідчить рівність :

. (9.17)

Незначні відхилення викликані, як правило, округленням розрахунків. Парний лінійний коефіцієнт кореляції обчислимо за формулою 9.5:

r==,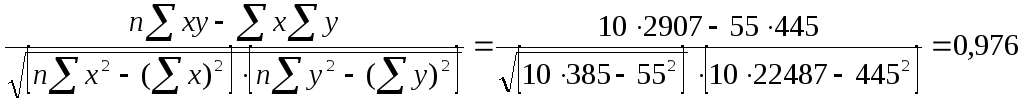

тобто, зв’язок між вартістю основних фондів і обсягом товарної продукції дуже сильний (див. таблицю 9.1)

Середню помилку апроксимації розрахуємо за формулою 9.7:

.

В економічних дослідженнях значення середньої помилки не повинно перевищувати 10%.

Коефіцієнт еластичності розрахуємо за формулою 9.13:

E=a_{i .}

Згідно з інтерпретацією економічної суті коефіцієнтів регресії і еластичності зі зміною величини основних фондів на 1 млн. грн. обсяг товарної продукції зміниться на 5,6 млн. грн., а у відносному значенні – зі зміною вартості основних фондів на 1% обсяг продукції зміниться на 0,7%.

Оцінку коефіцієнтів регресії і еластичності доцільніше здійснювати в багатофакторних рівняннях.

4. Вирівнювання рядів динаміки. Часовий тренд

Нарівні з використанням методів укрупнення інтервалів, плинної середньої для вирівнювання динамічних рядів застосовуються також методи кореляції і регресії.

Динамічні ряди вирівнюються за допомогою залежності:

, (9.18)

де _t -рівні динамічного ряду, які обчислюються відповідним аналітичним виразом (рівнянням) в момент часу t.

Залежність 9.18 називається часовим трендом. Вона відображає зміну явища (процесу) в часі.

Часовий тренд може бути описаний різними рівняннями, вид яких визначається характером зміни динаміки показників.

Для реалізації рівняння тренда (визначення параметрів і характеристик) застосовуються ті ж формули, які використовуються і для парного рівняння регресії, тільки замість фактора “х” використовується час “t”.

Рівняння часового тренда застосовується для інтерполяції і екстраполяції рядів динаміки.

Інтерполяція дозволяє знайти рівень показника за відсутній період в межах ретроспективи: ; екстраполяція дозволяє прогнозувати рівень показників за межами ретроспективи: (т =1;2;3 і т.д.).

Розглянемо приклад реалізації лінійного рівняння тренда на підставі даних таблиці 9.3.

Таблиця 9.3 - Споживання кондитерських виробів за рік на одну

людину

N року	Споживання кондитерських виробів, кг.(y)	t	ty	t2	у2
1	10,7	1	10,7	1	114,5	10,60	0,10	0,009
2	11,5	2	23,0	4	132,3	11,55	0,05	0,004
3	12,2	3	36,6	9	148,8	12,50	0,30	0,025
4	13,4	4	53,6	16	179,6	13,45	0,05	0,004
5	15,0	5	75,0	25	225,0	14,40	0,60	0,040
6	15,0	6	90,0	36	225,0	15,35	0,35	0,023
Разом:	77,8	21	288,9	91	1025,2	77,85	-	0,105

Розрахуємо параметри рівняння:

;

.

Отже, рівняння тренда має вигляд:

y=9,65+0,95t.

Парний лінійний коефіцієнт кореляції дорівнює:

r= .

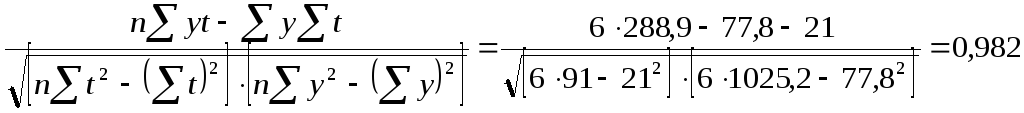Розрахункові значення функції на підставі побудованого рівняння:

;

;

;

;

;

.

Результати розрахунків записані у відповідну графу таблиці 9.3.

Середня помилка апроксимації дорівнює:

.

Значення парного лінійного коефіцієнта кореляції і середньої помилки апроксимації свідчать, що побудоване рівняння часового тренда відрізняється високими статистичними характеристиками. Це дозволяє застосувати рівняння для побудови прогнозу шляхом використання в рівнянні тренда значення: t = n+т (n = 6, т=5)

Прогнозні значення () на роки наступної п’ятирічки дорівнюють:

кг;

кг;

кг;

кг;

кг.

4. Непараметричні показники зв’язку

Методи кореляції і регресії орієнтовані на виявлення і оцінку

тісноти зв’язку між кількісними показниками.

Статистика одночасно оцінює наявність і вимірює тісноту зв’язку і між якісними показниками, для чого застосовуються непараметричні методи.

Серед значної кількості непараметричних методів розглянемо метод, який дозволяє досліджувати зв’язки паралельних рядів не на основі первинних даних, а на основі рангів.

Ранжування - це упорядкування досліджуваних об’єктів на основі переваг. Згідно з ранжуванням кожній одиниці сукупності присвоюється порядковий номер ряду, який надається їй за рівнем ознаки. Таким чином, ряд значень ознаки ранжується, а номер кожної окремої одиниці буде її рангом. Ранг – це порядковий номер значень ознак, установлений в порядку зростання або зменшення їх величин.

Для ранжованих об’єктів показником зв’язку є коефіцієнт рангової кореляції.

Серед непараметричних методів для визначення тісноти зв’язку між ознаками на практиці використовуються коефіцієнти рангової кореляції Спірмена () і Кендалла ().

Коефіцієнт рангової кореляції Спірмена обчислюється за такою формулою:

(9.19)

де n- кількість одиниць вибіркової сукупності ;

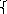d²=(R_x – R_y)² R_x – ранг факторної ознаки;

R_y – ранг результативної ознаки.