10.2. Телеграфные уравнения

Рассмотрим однородную двухпроводную длинную линию длиной 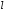(рис. 10.1а). С началом линии свяжем координатную ось.Электродинамическое состояние длинной линии будем описывать понятиями электрических цепей: напряжения 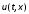и тока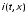, которые являются функциями времени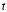и координаты. В линии выберем участок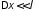, которому сопоставим эквивалентную электрическую цепь (рис.10.1б).

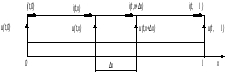
а)

б)

Рис. 10.1 Двухпроводная длинная линия:

а) графическое изображение;

б) эквивалентная схема участка длинной линии

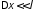
По законам Кирхгофа для этой цепи составим систему уравнений

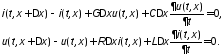(10.1)

Разделим оба уравнения на 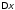, и, перейдя к его бесконечно малым приращениям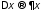,,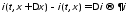, получим систему из двух уравнений в частных производных

(10.2)

Система уравнений (10.2) называется телеграфными уравнениями, что обусловлено исторически первым применение линий связи для передачи телеграфных сигналов. Таким образом, электрические процессы в длинной линии описываются системой из двух уравнений в частных производных для мгновенных значени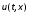й и , являющихся скалярными функциями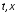. Для получения решения телеграфных уравнений в конкретном случае система уравнений в частных производных дополняется начальными условиями: , 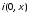и граничными условиями:,,,.

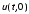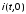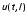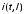10.3. Длинная линия. Гармонический волновой процесс

10.3.1. Общее решение телеграфных уравнений

_{Пусть имеется однородная двухпроводная длинная линия, которая возбуждается от генератора гармоническим колебанием с частотой} . В силу линейности системы в любом сечении линии колебания будут гармоническими. Гармонический процесс по определению не имеет начала и конца (действует при 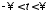_{). Поэтому общее решение при гармоническом возбуждении представим, используя метод комплексных амплитуд как}

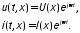_(10.3)

_{Поскольку по времени нам решение известно, то система уравнений (10.2) в частных производных переходит в систему обыкновенных дифференциальных уравнений, которая в комплексной форме примет вид}

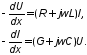_(10.4)

_{Здесь U(x) и I(x) – распределения комплексных амплитуд напряжения и тока вдоль длинной линии. Используя понятия погонного комплексного продольного сопротивления Z=R+jL и погонной комплексной поперечной проводимости Y=G+jC система (10.4) примет вид}

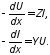_(10.5)

Система уравнений (10.5) в конкретном случае дополняется граничными условиями: U(0), I(0), U(l), I(l). Продифференцировав первое уравнение в (10.5) и подставив в него значение производной от тока по x второго уравнения, получим волновое уравнение

_(10.6)

где 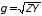–коэффициент распространения.

_{Общее решение уравнения (10.6) запишем в виде}

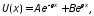. (10.7)

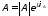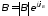где и– постоянные интегрирования, которые определяются из граничных условий. Из первого уравнения системы (10.5) находим распределение тока вдоль линии

_(10.8)

Здесь 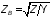– волновое сопротивление.

В общем случае коэффициент распространения 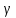и волновое сопротивление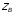величины комплексные:

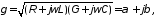(10.9)

где –коэффициент затухания; –постоянная распространения волны;

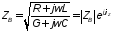. (10.10)

Они являются основными параметрами длинной линии и обычно используются вместо погонных параметров L, C, R, G.

В линии без потерь =0 и поэтому коэффициент распространения принимает мнимое значение

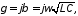(10.11)

а волновое сопротивление – вещественное значение, которое, как и характеристическое сопротивление колебательного контура обозначают символом

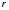
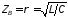. (10.12)

_{В линии с малыми потерями выполняются условия} и 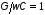. Учитывая малость этих параметров, выполним разложение формул (10.9) и (10.10) в ряд. После того как удержим в ряде два первых члена, получим приближенные выражения

(10.13)

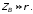(10.14)

Из формулы (10.13) можно видеть, что в линии с малыми потерям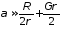и и.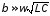

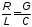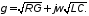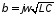Если в линии выполняются условия (условия Хевисайда), тоВ этом случае сигнал по линии передается без искажений:, волновое сопротивление не зависят от частоты, а постоянная распространения линейно зависит от частоты, что легко проверить подстановкой условия Хевисайда в (10.9) и (10.10).