Учебное пособие ТеорМех

С1x1y1z1, а через любую точку О на оси С1х1 – оси Oxyz так, чтобы Оу║С1у1, Oz ║C1z1 (Рис.10.5). Расстояние между осями Oz и C1z1 обо- значим через d. Тогда по формулам (10.3) получим:

JOz = åmk (x 2k + y2k ); JCz1 = åmk (x12k + y12k ) .

Из рисунка видно, что для любой точки тела

x k = x1k − d и x2k = x12k − 2x1k d + d2 , а yk = y1k . Подставляя эти зна- чения хк и ук в выражение для Joz и вынося общие множители d2 и 2d за скобки, получим:

JOz = åmk (x12k − 2x1kd + d2 + у12к ) =

= åmk (x12k + у12к ) + å(mk )d2 − å(mk x1k )2d

Здесь åmk (x12k + y12k ) = JCz1 , å(mk ) = M . Найдем å(mk x1k ).

На основании формул (10.1), для координат центра масс справедливо:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями (теорема Гюйгенса) .

§5. Дифференциальные уравнения движения системы

Рассмотрим систему, состоящую из n точек. Выделим любую точку системы с массой mк. Обозначим равнодействующую всех при-

ложенных к точке внешних сил Fke , а равнодействующую внутренних сил Fki . Если при этом точка имеет ускорение ak , то по второму зако-

131

mnan = Fne + Fni

Эта система представляет дифференциальные уравнения движе- ния системы в векторной форме. Спроектировав эти равенства на ка- кие-нибудь координатные оси, получим уравнения движения системы в проекциях на эти оси.

Полное решение задачи динамики для системы будет заключать- ся в том чтобы, зная заданные силы и наложенные связи, определить закон движения каждой точки системы. Это очень сложная задача.

Однако при решении многих задач необходимость находить за- кон движения каждой точки не возникает. Достаточно найти какие-то характеристики, определяющие движение системы в целом. Для этого применяют методы, которые основаны на общих теоремах динами-

ки системы.

§6. Теорема о движении центра масс

В ряде случаев для определения характера движения системы (например, твердого тела) требуется знать закон движения ее центра масс. Чтобы найти этот закон, сложим почленно уравнения системы (10.4). Тогда получим:

Преобразуем левую часть этого уравнения. Из уравнения (10.2) имеем: Mrc = åmk rk . Беря от обеих частей этого равенства вторую

производную по времени и замечая, что производная суммы равна сумме производных, найдем:

где ac – ускорение центра масс системы. Так как по первому свойству внутренних сил åFki = 0, с учетом (10.6) из (10.5) получим:

132

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.

Проектируя обе части полученной теоремы на координатные оси, получим:

Значение доказанной теоремы состоит в следующем:

1.Решения, которые мы получаем, рассматривая тело как материальную точку, определяют закон движения центра масс этого тела.

2.Теорема позволяет исключать из рассмотрения все неизвестные внутренние силы.

§7. Закон сохранения движения центра масс системы

1. Если åFkе = 0 , то центр масс системы движется с постоянной по модулю и направлению скоростью.

2. åFkех = 0, то проекция скорости центра масс на данную ось

постоянна.

Эти результаты выражают закон сохранения движения центра масс.

Отсюда следует закон сохранения положения центра масс системы:

1. ЕслиåFkе = 0 и скорость центра масс в какой-то момент вре- мени равна нулю, то положение центра масс системы не изменяется.

2. Если åFkех = 0 и проекция скорости центра масс на некото-

рую ось х в какой-то момент времени равна нулю, то координата х центра масс системы не изменяется.

Рассмотрим следующий пример . Пусть тело массой m скатывается по плоскости треугольника массой M, лежа- щего гладкой горизонтальной поверхности. Требуется опре- делить, на сколько переместится треугольник в горизон-

тальном направлении (ось х), если указанное тело пройдет путь L (рис.10.7). Так как в направлении движения внешние силы отсутст-

133

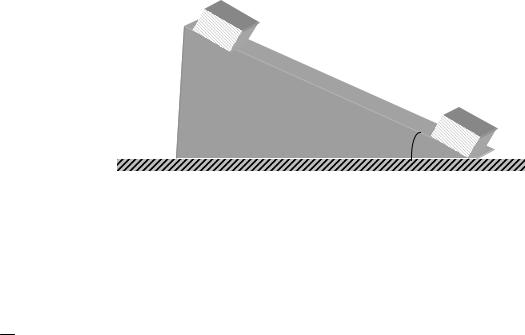
вуют, и начальная скорость центра масс равна нулю, то координата х центра масс не меняется, то есть: Mcxc = const . Отсюда получа-

ем, что

где х1 и х2 – координаты центры масс тел в первом положении, х3 и х4 – координаты центры масс тел во втором положении. Обозначим

§8. Количество движения системы

Количеством движения системы будем называть векторную величину Q , равную геометрической сумме (главному вектору)

количеств движения всех точек системы.

Вычислять количество движения системы по указанной формуле неудобно, так как для этого приходится определять массы и скорости каждой ее точки. Упростим эту формулу.

Как говорилось выше, при изучении динамики системы матери-

альных точек нет необходимости изучать движение каждой точки в

134

отдельности. Достаточно знать некоторые суммарные характеристи- ки системы в целом. Одной из таких характеристик является центр масс системы. Его положение, как было показано выше, определяется радиус-вектором

Умножим обе части этого уравнения на åmk и, учитывая, что åmk = М , получим

Мrc = åmk rk .

Беря от обеих частей производную по времени, получим

Мvc = Q

т.е. количество движения системы равно произведению мас-

сы всей системы на скорость ее центра масс.

Из этой формулы следует, что если центр масс не движется, то количество движения равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.

Если движение тела является сложным, то величина Q не будет зависеть от его вращательного движения вокруг центра масс. Таким образом, количество движения можно рассматривать как характери- стику поступательного движения тела.

§9. Теорема об изменении количества движения системы

Сложив почленно дифференциальные уравнения в системе (10.4),

получим

135

Производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внеш-

них сил. В проекциях на координатные оси будет:

Найдем другое выражение этой теоремы. Пусть в момент време- ни t=0 количество движения системы равно Qо , а в момент t1 стано- вится Q1. Тогда, умножая обе части равенства (10.11) на dt и, интег- рируя полученное выражение, получим:

t1

Q1 − Qо = åò Fkedt .

0

Так как интегралы, стоящие справа дают импульсы внешних сил

Уравнение (10.12) выражает теорему об изменении количества движения системы в интегральной форме: изменение количества

движения системы за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени.

В проекциях на координатные оси будет

Q1х − Qох = åSekх; Q1y − Qоy = åSeky; Q1z − Qоz = åSekz .

§10. Закон сохранения количества движения системы

Из теоремы об изменении количества движения системы можно получить следующие важные следствия.

1.Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению:

åFкe = 0, то Q = сonst .

2.Если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось постоянная величина.

136

åFкхe = 0 , то Qх = сonst .

Эти результаты выражают закон сохранения количества дви-

жения системы.

Рассмотрим следующий пример , похожий на пример из §7. Пусть треугольник массой M движется вдоль горизонталь- ной оси х со скоростью v. В некоторый момент тело массы m начинает двигаться по наклонной плоскости треугольни-

ка с относительной скоростью u. Требуется определить новую ско- рость треугольника v1 (рис.10.8). Так как в направлении движения

внешние силы

отсутствуют, то Mcvc = const . Отсюда получаем, что

Рис. 10.8

Если m → 0 или u → 0, то v = v1 , то есть при малой массе те- ла или его скорости скорость треугольника практически не меняет- ся. Если M → ∞ , то v = v1 , то есть при очень большой массе тре- угольника скорость треугольника также практически не меняется.

Если v = mu cos α , то треугольник остановится. Из формулы (10.14)

M + m

следует также, что при достаточно больших значениях относи- тельной скорости u, направление движения треугольника может измениться на противоположное.

137

§11. Главный момент количеств движения системы (кинетический момент)

Кинетическим моментом системы относительно данного центра О называется величина Ko , равная геометрической сумме

моментов количеств движения всех точек системы относительно этого центра:

Ko = åmo (mk vk ) .

Кинетический момент системы можно рассматривать как ха-

Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

§12. Теорема об изменении кинетического момента системы

Теорема: производная по времени от главного момента коли-

честв движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра.

Для одной точки системы верно следующее равенство

138

dtd mo (mk vk ) = mo (Fke ) + mo (Fki ),

тогда для всей системы получим

dtd [åmo (mk vk )]= åmo (Fke ) + åmo (Fki ) ,

но åmo (Fki ) = 0 по свойству внутренних сил. Поэтому, учиты-

В случае вращения твердого тела относительно оси z, когда все силы, действующие на него, являются внешними, формула (10.15)

Это уравнение называется уравнением вращения твердого тела.

§13. Закон сохранения кинетического момента

Если åmo (Fke ) = 0, то Ko = const , т.е. если сумма моментов

относительно данного центра всех приложенных к системе внешних сил равна нулю, то кинетический момент системы относительно этого центра будет постоянен и по модулю и по направлению.

Если åmz (Fke ) = 0 , то Kz = const , т.е. если сумма моментов

всех действующих на систему внешних сил относительно какойлибо оси равна нулю, то кинетический момент относительно этой оси будет величиной постоянной.

Эти результаты выражают закон сохранения кинетического мо- мента.

Рассмотрим систему, вращающуюся вокруг неподвижной оси z. Тогда ее кинетический момент будет равен Kz = Jzω. Если

åmz (Fke ) = 0 , то Jzω = const .

Отсюда приходим к следующим выводам:

139

- если система абсолютно твердая, то ее Jz = const , а следова-

тельно постоянна и ее угловая скорость.

- если система изменяема, то под действием внутренних сил отдельные ее точки могут удаляться от оси, что вызывает увеличение Jz , или приближаться к оси, что приводит к уменьшению

Jz . Но, так как Jzω = const , то в первом случае ω будет умень-

шаться, а во втором увеличиваться.

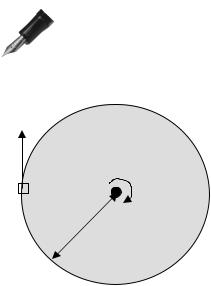
Рассмотрим следующий пример. Пусть однородный диск радиуса R и массой M=2m вращается вокруг вертикальной оси z с угловой скоростью ω. В некоторый момент тело мас- сы m начинает двигаться вдоль обода диска с относитель-

ной скоростью v (рис.10.10 - вид сверху). Требуется определить новую

ется, а при v = 2ωR диск остановится. Более того, при v > 2ωR диск начнет вращаться в обратном направлении.

§14. Кинетическая энергия системы.

Кинетической энергией системы называется скалярная величина Т, равная сумме кинетических энергий всех точек системы:

140