
Учебное пособие ТеорМех
.pdf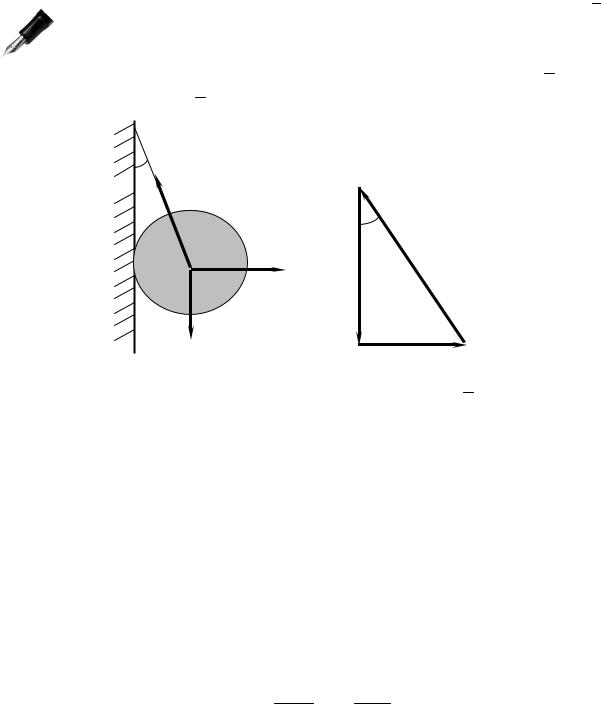
менением тригонометрических соотношений для определения сторон полученного многоугольника.
Приведем следующий элементарный
Пример. Пусть некоторое сферическое тело D весом P подвешено на невесомой нерастяжимой нити, как это пока- зано на рис.2.4а. Требуется определить силу натяжения ни-
ти и реакцию стенки. Обозначим силу натяжения нити через T , силу реакции стенки через N , угол наклона нити к вертикали – через α.
 α
α
T
T |
α |
N
D
P |
P |
N |
Рис. 2.4б |
|
|
Рис. 2.4а |
|
|
|
|
Отметим, что, хотя точка приложения силы N находится на самой стенке, мы на чертеже перенесли ее вдоль линии действия. Так как тело D находится в равновесии, то векторная сумма указан- ных трех сил должна быть равна нулю, а это означает, что сило- вой треугольник будет замкнут. Построение (рис.2.4б) мы начи- наем с известного вертикального отрезка, равного в выбранном масштабе заданной величине P . Затем из конца этого отрезка про- водится горизонтальная прямая, соответствующая силе N . Величи- на этой силы нам неизвестна, но известен тот факт, что третья
сторона треугольника должна проходить под углом α к вертикали и заканчиваться в начале первого отрезка. Из прямоугольного тре- угольника (рис.2.4б) мы можем определить гипотенузу и один из не- известных катетов по формулам:
T= cosPα ; N= sinPα .
Интересен тот факт, что, так как cosα <1, натяжение троса оказывается больше веса тела.
Рассмотрим сейчас интересный факт, который носит название тео-
ремы о трех силах. Если тело находится в равновесии под действием трех непараллельных сил, то эти силы сходятся в одной точке.
21

Доказательство этого факта элементарно. Представим себе, что на тело действует две непараллельные силы F1 и F2 (рис 2.5). Тогда, перенеся эти силы в общую точку приложения и сложив их, мы полу- чим равнодействующую этих двух сил – R12 . Но тогда, для того что-
F1 




 R12
R12
F 2
2
F3
Рис. 2.5
бы третья сила F3 могла соз-
дать условия равновесия данного тела, она должна располагаться на линии дей- ствия силы R12 , быть проти-
воположной ей по направле- нию и равной по величине. Поэтому, как видно из рис 2.5, система сил F1 , F2 иF3 – сходящаяся.
Пример. Рассмотрим равновесие балки весом P шарнир- но закрепленной в стенке и поддерживаемой тросом, как это показано на рис.2.6. Вес P приложен к середине балки (в ее центре тяжести). На балку также действует сила натя- жения троса и реакция в шарнире А. Согласно последней теореме
реакцию шарнира мы направляем так, чтобы ее линия действия про- ходила через точку пересечения линий действий сил веса и реак- ции нити. Отметим, что если изменять угол подвеса нити к стенке, то направление силы реакции в шарнире будет изменяться, что было уже указано ранее, когда рассматривался вопрос о направлении силы реакции неподвижного шарнира.
R 
 T
T
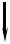 P
P
Рис. 2.6
22

§3. Аналитическое условие равновесия сходящейся системы сил
Как уже было показано в предыдущем подразделе, условие рав- новесия сходящейся системы сил записывается с помощью следую-
n
щей формулы: åFi =0 . Геометрическое использование этого равенст-
i=1
ва часто становится неудобным, потому что влечет необходимость аккуратных построений. В связи с этим, чаще применяется метод ис- следования равновесия с помощью некоторых аналитических соот- ношений, позволяющий определять неизвестные силы из определен- ных уравнений.
В плоском случае, о котором сейчас идет речь, можно спроекти- ровать последнее векторное равенства на оси координат X и Y. Как известно из курса математики, проекция суммы векторов на некото- рую ось равна сумме проекций этих векторов на эту ось. Тогда урав- нения равновесия примут вид:
ïìåFix = 0 |
|
n |
|
ï i=1 |
(2.3) |
í n |
|
ïïåFiy = 0 |
|
î i=1 |
|
Для того чтобы мы могли воспользоваться этими соотношения- ми, вспомним, как проектируются силы на оси координат (рис.2.7). Обычно при задании силы указывается угол с какой-либо осью коор- динат. В плоском случае задание одного такого угла полностью опре- деляет направление силы. Проекция силы F на ось, с которой задан угол, будет равна Fcosα, а на ось ей перпендикулярную – Fsinα.
F
y
x
Fsinα |
α |
|
Fcosα
Рис. 2.7
23
Отметим, что значение проекций сил на оси координат не зависит от линий их действия, а зависит только от величин и направлений этих сил. Действительно, как показано на рис.2.8, проекции сил F1 и
F2 на оси координат x и y принимают одинаковые значения.
Y
F2
F2sinα |
α |
|
|
F1 |
F1sinα |
|
α |
X |
|
|
F1cosα |
F2cosα |
Рис. 2.8
Пример. Как известно из курса физики, сила трения скольжения Fтр равна произведению коэффициента трения f на величину нормальной реакции поверхности N, по которой движется тело. Требуется определить связь между коэффи-
циентом трения и углом наклона плоскости, при котором тело бу- дет скользить по ней равномерно (рис.2.9).
Y
Fтр N
α |
X |
|
mg |
|
α |
Рис. 2.9 |
|
Составим уравнения равновесия, спроектировав все силы на оси X и Y соответственно.
mg sin α − Fтр = 0, N − mg cos α = 0 .
24
Выражая отсюда N и учитывая, что Fтр=fN, получаем, что
Fтр = fmg cos α .
Тогда |
mgsinα − fmgcosα = 0. |
Сокращая на mg, |
получаем, что |
f = tgα . |
|
|
|
Таким |
образом, если угол |
α удовлетворяет |
соотношению |
α = arctgf, то тело будет скользить по наклонной плоскости равно- мерно.
Вопросы для самопроверки
1.Что такое система сходящихся сил ?
2.Как определить равнодействующую системы сходящихся сил ?
3.Что называют главным вектором системы ?
4.Приведите формулы для вычисления главного вектора.
5.В чем заключаются условия и уравнения равновесия системы сходящихся сил ?
6.Поясните алгоритм приведение системы сходящихся сил к простейшему виду.
7.Сформулируйте теорему о трех силах.
8.Как определяются проекции сил на координатные оси ?
25

ГЛАВА III. ПЛОСКАЯ СИСТЕМА СИЛ.
§ 1. Приведение к простейшей системе
В ряде случаев оценка силового воздействия на некоторое тело требует рассмотрения положения линии действия силы по отноше- нию к нему. Простейшим примером такой ситуации является попытка откручивания гайки, которая никак не хочет откручиваться. Извест- ным техническим приемом является желание увеличить длину ключа, например, с помощью подходящей трубы. Отметим, что при этом ве- личина силы не изменяется, однако пресловутая гайка может быть от- кручена. Таким образом, к величине силы добавляется еще и тот факт, насколько удалена линия действия силы от объекта воздействия.
Дадим следующее определение. Моментом силы относитель-
но точки (центра момента) называется скалярная величина, равная произведению величины силы на плечо, где плечо – это расстояние от точки до линии действия силы. На рис.3.1 показано плечо h силы F относительно точки А. Моментом силы F относи-
тельно точки А будет являться величина
|
F |
mA = Fh . |
|
90o |
Следует отметить, что так как момент силы |
||
|
|||
h |
|
является алгебраической величиной, то следует |
|
|
определить его знак. Условимся считать, что |
||
|
|
||
A |
|
момент будет иметь знак “+”, если сила совер- |
|
|
шает вращение вокруг точки А против часовой |
||
Рис. 3.1 |
|
||
|
стрелки и “-” – в противном случае. |
||
|
|
Отметим тот очевидный факт, что если |
точка лежит на линии действия силы, то момент силы относительно этой точки равен нулю.
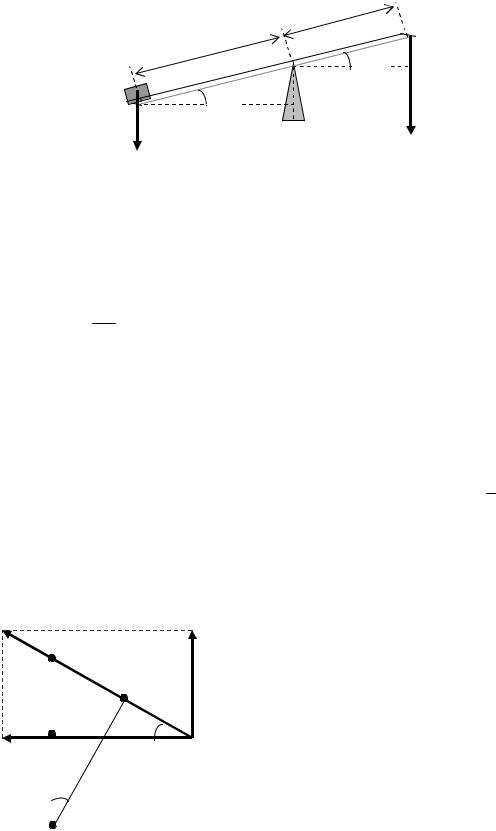
Рассмотрим следующий пример. На рис.3.2 изображен рычаг,
на одном из концов которого расположен груз веса P . Требу- ется определить, при какой величине силы F рычаг будет на-
ходиться в покое или вращаться относительно точки опоры А равномерно. Размеры и углы приведены на рисунке.
26
|
L2 |
L1 |
α |
|
|
α |
A |
|
F |
P
Рис. 3.2
Заметим, что момент силы, старающийся повернуть рычаг против часовой стрелки, равен PL1cosα, а момент, старающийся по-
вернуть рычаг по часовой стрелки, равен FL2cosα . Таким образом, для равновесия необходимо, чтобы PL1cosα = FL2cosα . Отсюда сле-
дует, что F = P L1 . Мы получили известное из курса физики соотно-
L2
шение между силами и рычагами.
К сожалению, часто достаточно трудно бывает непосредственно определить величину плеча силы. Помочь в этом может следующая теорема.
Теорема Вариньона: момент равнодействующей двух сил равен сумме моментов ее составляющих.
Доказательство. На рис.3.3 показаны разложение силы F на со- ставляющие и центр момента–точка А. Будем обозначать момент со- ставляющей Fcosα через m1, а момент составляющей Fsinα через m2.
Момент же силы |
F |
будет обозначаться через m. |
|
|||||
|
|
|
|
|
|
Отметим, что AD=h1, OD=h2, |
||
F |
|
|
AC=h. |
Тогда |
BD=h2tgα. |
|||
|
B |
|
|
AB=h1+h2tgα, h=ABcosα. Поэтому |
||||
|
|
|
C |
Fsinα |
|
h=h1сosα+h2sinα. Так как момент |
||
|
|
|
|
|||||
|
|
|
|
равнодействующей равен Fh, а мо- |
||||
|
|
|
|
|
|
|||
|
D |
α |
|
менты |
составляющих |
- соответст- |
||
|
|
венно |
Fcosαh1+Fsinαh2, то мы полу- |
|||||
Fcosα |
|
|
|
|
O |
|||
|
|
|
|
|||||
h |
|
чаем: Fh = F(cosαh1+sinαh2), что тре- |
||||||
h1 |
|
|
||||||
|
|
бовалось доказать. |
|
|||||
α |
|
|
|
|||||
|
|
|
h2 |
|
|
Из этой теоремы вытекает оче- |
||
A |
|
|
|
|
видное следствие, что момент рав- |
|||
|
|
|
|
|
||||
|
Рис. 3.3а |
|
|
нодействующей сходящейся сис- |
||||
|
|
|
темы сил равен сумме моментов ее |
|||||
составляющих.
27
§ 2. Пары сил. Свойства пар
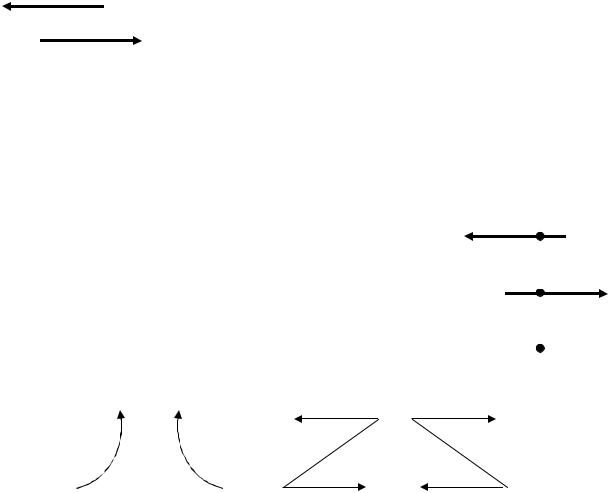
Одним из очень важных понятий статики является понятие пары сил, под которой подразумеваются две равные по величине,
противоположные по направлению силы, имеющие разные линии действия. На рис.3.4 показана пара сил, каждая из которых имеет ве- личину F. Если формально сложить эти силы, то их равнодействую-
щая равна нулю, но понятно, что эти две силы обязательно окажут |
||
|
воздействие на некоторое тело. Вполне очевидно, |
|
|
что это действие будет сводиться к попытке по- |
|
|
вернуть это тело. Самый простой пример указан- |
|
Рис. 3.4 |
ного воздействия – это управление рулем автомо- |
|
биля. Если при этом одна рука не высунута из ок- |
||
|
||
на, то обычно силовое воздействие на руль – это пара сил. |
||
Рассмотрим момент пары сил относительно произвольно взятой точки О. Этот момент равен F×OB - F×OA = F× AB. (рис.3.5). Рас- стояние между силами АВ называется плечом пары сил. Таким обра- зом, момент пары сил не зависит от положения центра момента и ра-
вен произведению одной из сил пары на ее плечо. |
|
|
|
||||
Этот факт говорит о том, что пару сил можно про- |
B |
|
|
||||
|
|||||||
извольным образом перемещать на плоскости, не |
A |
|
|
||||
изменяя величин сил и плеча пары. |
|
|
|
|
|||
|
|
|
|
|
|||
Рассмотренное выше указывает на тот факт, что |
|
|
|
||||
действие пары сил характеризуется моментом этой |
O |
|
|
||||
пары, в связи с чем ее действие будет обозначаться |
|
|
|||||
Рис. 3.5 |
|||||||
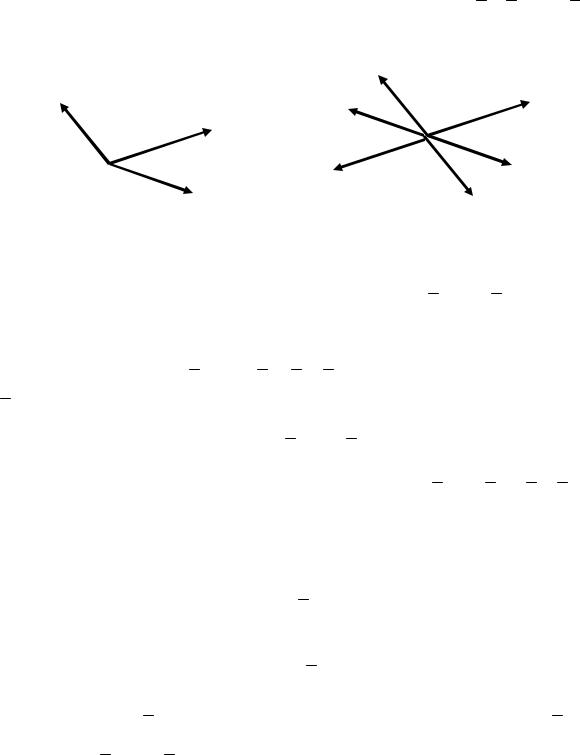
одним из следующих символов (рис 3.6): |
|
|
|||||
|
|
|
|
|
|||
М |
М |
М |
М |
|
|
|
|
|
|
|
|
|
|||
Рис. 3.6
Так как момент пары – алгебраическая величина, то необходимо условиться о его знаке. Так же как и для момента силы условимся считать, что момент пары будет иметь знак “+”, если пара стара-
ется повернуть плоскость чертежа против часовой стрелки и “-“
– в противном случае.
Так как результат действия пар сил на тело характеризуется воз- действием на него моментов пар, то сложение пар производится ал- гебраическим сложением моментов этих пар, в результате чего сово- купность пар сил приводится к равнодействующей паре.
28
§ 3. Приведение произвольной плоской системы сил к простейшему виду
Представим теперь себе некоторое множество сил F1 , F2 , …, Fn , произвольно расположенных на некоторой плоскости (рис.3.7).
F1 |
Fn² |
F2¢ |
|
F2 |
A |
|
|
|
|
F2² |
Fn¢ |
A |
Fn |
F1² |
|
||
|
|
|
|
|
F1¢ |
|
|
Рис. 3.7 |
Выберем некоторую точку А, которую назовем точкой приведе- ния и приложим в этой точке совокупности сил { Fi' } и { Fi'' }, как это
показано на рисунке. Очевидно, что эти совокупности сил имеют рав- нодействующую, равную нулю, что означает эквивалентность сле-
дующих систем сил: { Fi } {Fi , Fi' , Fi'' }. Так как совокупность сил { Fi' } – сходящаяся, то она приводится к равнодействующей
n
R' = åFi' .
i=1
Этот факт дает следующую эквивалентность: {Fi } R' +{ Fi , Fi'' }.
Как видно из рис.3.7, последняя совокупность сил представляет собой совокупность пар сил и, следовательно, может быть приведена
к равнодействующей паре с моментом
n
m=åmA (Fi ).
i=1
Отметим, что при изменении положения точки приведения А, мы
получим другое положение вектора R' на плоскости, хотя величина и направление его останутся неизменными. Это следует из того, что
при определении R' фактически складывается совокупность сил { Fi }.
n
Вектор R = åFi называется главным вектором системы сил,
i=1
как угодно расположенных на плоскости, сумма же моментов этих сил относительно точки А называется главным моментом относи-
29

тельно точки А. С учетом этих терминов полученный выше результат можно сформулировать следующим образом:
Силы, расположенные как угодно на плоскости, могут быть при- ведены к силе, равной их главному вектору и приложенной в произ- вольной точке А, и к паре, момент которой равен главному моменту данных сил относительно точки А.
§4. Условия равновесия произвольной плоской системы сил
Для того чтобы тело находилось в равновесии, необходимо и
достаточно выполнение следующих условий
|
|
n |
n |
|||
|
|
' = å |
Fi' = 0 , |
|
|
|
R |
m = åmA (Fi ) = 0 . |
|||||
|
|
i=1 |
i=1 |
|||
Спроектировав первое из этих равенств на оси координат, полу-
чаем следующее условие равновесия произвольной плоской системы сил:
ïìåFix |
= 0; |
|
n |
|
|
ï i=1 |
|
|
ï n |
= 0; |
(3.1) |
íåFiy |
||
ï i=1 |
|
|
ï n |
r |
|
ïåmA (F) |
= 0. |
|
î i=1 |
|
|
Можно доказать, что возможны другие формы уравнений равно- весия.
Второй формой является равенство нулю алгебраических сумм моментов всех сил относительно двух любых точек и равенство нулю алгебраической суммы проекций всех сил на ось, не перпендикуляр- ную прямой, проходящей через выбранные точки, т.е.
å mA (Fk )= 0; å mB (Fk )= 0; å Fkx = 0; Ось х не ^ АВ.
Действительно, первые два из предыдущих равенств гарантиру- ют равенство нулю главного момента системы сил, но при этих усло- виях главный вектор может лежать на прямой АВ. Третье же условие обязывает этот вектор быть равным нулю, так как ось х не ^ АВ.
Третьей формой является равенство нулю алгебраических сумм моментов сил относительно любых трех точек, не лежащих на одной прямой, т.е.
30
