Учебное пособие ТеорМех

вестно, то координаты центра тяжести можно вычислить по выве- денным выше формулам для центра тяжести объема, плоской фигу- ры, линии. При этом число слагаемых в каждой из сумм будет рав- но числу частей, на которые разбито тело.

3.Дополнение. Этот способ является частным случаем спосо- ба разбиения. Он применяется к телам, имеющим вырезы, если цен- тры тяжести тела без выреза и вырезанной части известны. В этом случае используются те же формулы, что и в методе разбиения, но объемы, площади вырезанных частей считаются отрицательными.

4.Центры тяжести неоднородных тел сложной конфигурации определяют экспериментально методами подвешивания или взве- шивания.

§7. Центры тяжести некоторых однородных тел 1. Центр тяжести дуги окружности.

Рассмотрим дугу АВ радиуса R с центральным углом АОВ = 2α (рисунок 5.7). В силу симметрии центр тяжести этой дуги лежит на биссектрисе центрального угла, которую примем за ось х, выбрав начало координат в центре окружности.

Выделим на дуге АВ элемент ММ' длиной dL=Rdφ, положение которого определяется углом φ. Координата х элемента ММ' x=Rcosφ. Координата центра тяжести линии определяется форму- лой:

xC = L1 òL xdL,

где длина дуги L=R·2αрад . Подставляя значения x, dl в формулу, по- лучаем:

Итак, центр тяжести дуги окружности лежит на биссектрисе

61

центрального угла на расстоянии от центра окружности

В

Рис. 5.7

2. Центр тяжести треугольника

Разобьем площадь треугольника АВD (рис. 5.8) прямыми, парал- лельными стороне AD, на n узких полосок, каждую из которых можно рассматривать как отрезок прямой; все центры тяжести этих полосок лежат в серединах этих полосок, т.е. на медиане ВЕ треугольника. Сле- довательно, и центр тяжести всего треугольника лежит на медиане.

B

C

A E D

Рис. 5.8

62

Аналогичный результат получается для двух других медиан.

Поэтому центр тяжести треугольника лежит в точке пересечения его медиан, при этом

EC = 13 BE .

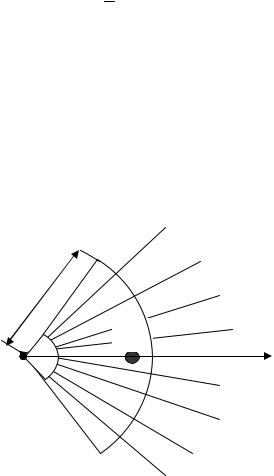
1. Центр тяжести кругового сектора

Рассмотрим круговой сектор ОАВ радиуса R с центральным уг-

лом 2α (рис. 5.9).

Разобьем дугу АВ на большое число n равных отрезков и в точки деления проведем радиусы. Сектор ОАВ оказывается разби- тым на n равных секторов, каждый из которых можно рассматри- вать как треугольник.

B

2R

3

A

Рис. 5.9

Все центры тяжести этих треугольников лежат на дуге 23 R и при n→∞ равномерно заполняют эту дугу. Следовательно, центр тяже- сти сектора ОАВ совпадает с центром тяжести дуги радиуса 23 R .

Окончательно получим, что центр тяжести кругового сектора лежит на биссектрисе угла на расстоянии от центра круга 23 R .

63

Вопросы для самопроверки:

1.Как определить центр тяжести тела?

2.Как найти центр тяжести объема?

3.Запишите формулы для определения центра тяжести плоской фигуры?

4.Что называют статическим моментом плоской фигуры относительно оси?

5.Поясните как определяется центр тяжести линии.

8.Обоснуйте положение центра тяжести треугольника.

9.Как найти центр тяжести кругового сектора?

64

РАЗДЕЛ ВТОРОЙ.

КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА

ГЛАВА VI. КИНЕМАТИКА ТОЧКИ

§1. Введение в кинематику

Кинематикой называется раздел теоретической механики, в ко-

тором изучаются геометрические свойства движения материальных точек или тел без учета их массы и действующих на них сил.

Под движением в механике понимается изменение с течением времени положения данного тела в пространстве по отношению к другим телам.

Для изучения этого движения в разные моменты времени с телом, относительно которого оно изучается, связывают систему координат, которая образует с этим телом систему отсчета.

Изучение кинематики начнем с изучения простейшего объекта – материальной точки.

Движущаяся точка описывает в пространстве некоторую линию. Эта линия, представляющая собой геометрическое место последова-

тельных положений движущейся точки в рассматриваемой системе отсчета, называется траекторией движения точки.

Если траектория – прямая линия, то движение называют прямо-

линейным, а если кривая – криволинейным.

Основная задача кинематики точки заключается в том, чтобы

по известному закону движения точки определить кинематические характеристики ее движения.

§2. Способы задания движения точки

Для задания движения точки применяют один из трех способов:

65

положительное и отрицательное направления отсчета. Положение точки определяется криволинейной (дуговой) координатой ОМ=s.

При движении точки М значение s будет постоянно изменяться. Следовательно, чтобы знать положение точки на траектории в любой момент времени, надо знать зависимость s = f (t) - закон движения

точки М вдоль траектории.

Величина s определяет положение точки, а не пройденный ею путь. Например, если точка, двигаясь из начала 0, доходит до поло- жения М0, а затем, перемещаясь в обратном направлении, приходит в положение М, то в этот момент ее дуговая координата s=0М, а прой- денный за время движения путь будет равен 0М0+М0М. Дуговая ко- ордината может быть равна пути только в том случае, если точка движется из начала 0 в положительную сторону.

Векторный способ задания движения точки

Пусть точка М движется по отношению к некоторой системе от-

форме. Траектория точки является геометрическим местом концов радиуса вектора r движущейся точки.

Линию, образованную концами переменного вектора, начало ко- торого находится в определенной точке пространства, называют годографом этого вектора. Следовательно, траектория точки М явля- ется годографом ее радиуса-вектора r .

Задать вектор можно аналитически его проекциями на коорди- натные оси. В прямоугольных декартовых координатах для вектора r будет: rx = x, ry = y, rz = z , где x,y,z – декартовы координаты точки.

Тогда, если ввести единичные векторы (орты) i, j,k координатных осей, получим выражение: r = ix + jy + kz .

66

Кроме того, вектор можно задать и другими способами, напри- мер, его модулем и углами с осями.

Координатный способ задания движения

Положение точки М в системе отсчета Охуz определяется тремя декартовыми координатами точки x,y,z. При движении точки М ее координаты меняются с течением времени. Следовательно, координа- ты x,y,z движущейся точки М являются функциями от времени t: х = f1 (t), у = f2 (t), z = f3 (t) - уравнения движения точки в декарто-

вых координатах. Движение точки М в одной плоскости определяется двумя уравнениями движения: х = f1 (t), у = f2 (t) . При прямолиней-

ном движении достаточно одного уравнения: х = f1 (t).

Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметрические уравне- ния траектории точки.

При исключении параметра t из уравнений движения получаются

эллипса сдвинут на 1 в «+» по оси х и на 3 в «+» по оси у (рис.6.3).

67

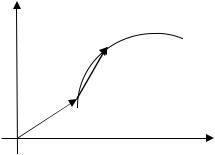
§3. Определение скорости точки при задании ее движения векторным способом

Скорость – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.

течение которого произошло это перемещение, представляет собой

Направление вектора vср совпадает с направлением r . Однако дан-

ное движение возможно лишь в случае очень малого расстояния ММ1 (иначе эта хорда не совпадает с траекторией движения), т.е. при уменьшении промежутка времени t и приближении его к нулю век- тор r также стремится к нулю, а вектор vср – к некоторому пределу.

Этот предел является вектором скорости точки в момент времени t:

Таким образом, вектор скорости точки в данный момент вре-

мени равен производной от радиуса-вектора точки по времени.

Вектор vср направлен по хорде ММ1 в сторону движения точки.

Когда t стремится к нулю, точка М1 стремится к точке М, т.е. пре- дельным положением секущей ММ1 является касательная.

Из этого следует, что вектор скорости точки v направлен по ка- сательной к траектории в сторону движения точки.

68

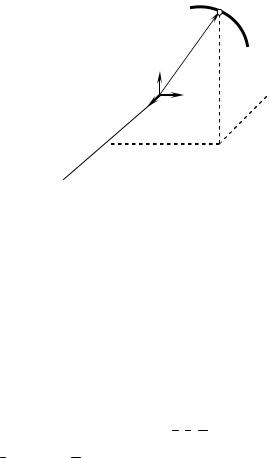
§4. Определение скорости точки при задании ее движения естественным способом

точек имеют следующие значения:

s = OM; s1 = OM1 = OM + MM1 = s + s ,

где ∆s – приращение дуговой координаты.

Проведем из произвольного центра О’ в точку М радиус-вектор r и определим скорость точки в момент t по формуле: v = ddtr .

Очевидно, что r зависит от дуговой координаты, и каждому зна- чению s соответствует свое значениеr . Таким образом, r можно рас- сматривать как функцию не только от времени, но и от дуговой коор- динаты r = r(s) . Тогда

правление стремится к направлению касательной, проведенной из

екцию скорости v на касательную, т.е. определяет алгебраическую величину скорости.

v = dsdt - модуль скорости равен абсолютному значению произ-

водной от дуговой координаты точки по времени.

69