Учебное пособие ТеорМех

ности Земли вертикально вверх. Тогда уравнения (9.7) примут вид:

2) Пусть v0 = 0, α = –90o. Это значит, что точка отпущена с высоты h вертикально вниз. Тогда уравнения (9.7) примут вид:

рость приземления.

3) Пусть h= 0. Это значит, что точка брошена с поверхности Земли под углом к горизонту. В самой дальней точке полета y=0, от-

Для определения угла α, соответствующего наибольшей дальности

что cos2α=0, откуда α=450.

§ 5. Теорема об изменении момента количества движения точки

При решении некоторых задач вместо самого вектора количества движения mv рассматривают его момент относительно некоторого центра или оси. Этот момент определяется аналогично моменту силы.

111

Моментом количества движения точки относительно некоторого центра О называется векторная величина mo (mv) определяемая ра-

где r - радиус-вектор движущейся точки, проведенный из центра

О.

Вектор mo (mv) направлен перпендикулярно плоскости, прохо- дящей через mv и центр О, а модуль mo (mv) = mv × h .

Теорема: производная по времени от момента количества

движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.

Действительно, продифференцируем по времени выражение (9.8)

учитывая, что v × mv = 0, т.к. данные вектора параллельны, а ma = F , получим

dtd (r ´ mv) = r ´ F или dtd mo (mv) = mo (F).

§6. Работа силы. Мощность. Теорема об изменении кинетической энергии точки.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, используется понятие работы силы.

Элементарной работой силы F , приложенной в точке М

112

щении МоМ1 вычисляется как предел интегральной суммы соответст-

вующих элементарных работ

В последней формуле использовано два различных вида записи скалярного произведения векторов.

Работа силы на любом перемещении МоМ1 равна взятому вдоль этого перемещения интегралу от элементарной работы.

Если величина Fcos α постоянна, то

A(М0 М1 ) = Fcos α × s,

где s – перемещение МоМ1. Такой случай возможен, если сила F постоянна по модулю и направлению, а перемещение точки прямоли- нейно.

Единица измерения работы – 1 джоуль=1Н·м.

Мощностью называется величина, определяющая работу, со- вершаемую силой в единицу времени. Если работа совершается рав-

Мощность равна произведению касательной составляющей силы на скорость. Измеряется мощность в ваттах. 1 ватт=1 Дж/с.

Кинетической энергией материальной точки называется ска-

лярная величина T = mv2 2 , равная половине произведения массы

точки на квадрат ее скорости. Единицей измерения кинетической энергии является джоуль.

Рассмотрим материальную точку массой m, перемещающуюся из положения М1, где она имеет скорость v1 , в положение М2, где ее

Интегрируя на промежутке от М1 до М2, получаем

113

где А1.2 – алгебраическая сумма работ всех действующих на точ- ку сил при перемещении точки из положения М1 в М2. Таким обра-

зом, изменение кинетической энергии точки при некотором ее пе-

ремещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

§7. Потенциальные силы. Закон сохранения механической энергии

Область, во всех точках которой на материальную точку, в эту область помещенную, действует некоторая сила, называется силовым полем для данной силы.

Силовое поле является потенциальным, а соответствующая си- ла - потенциальной, если существует скалярная функция П(x,y,z)

зывается потенциалом силы F , или потенциальной энергией точки. Пусть некоторая сила F является потенциальной. Тогда с учетом

(9.9) работа этой силы может быть определена по формуле:

т.е. работа потенциальной силы не зависит от траектории пере- мещения точки из положения М0 в М1, а зависит только от значения потенциала в соответствующих точках.

В качестве первого из примеров рассмотрим поле си- лы тяжести. Направив ось z вертикально вверх, получаем:

∂∂Пx = −Fx = 0, ∂∂Пy = −Fy = 0, ∂∂Пz = −Fz = mg .

Этому условию удовлетворяет функция П = mgz. Тогда работа силы тяжести равна П(М0 ) − П(М1)= mgz0 − mgz1=mg(z0-z1)=

mg z, т.е. работа равна произведению силы тяжести на перепад высоты.

В качестве второго примера рассмотрим поле силы упругости пружины. Направив ось x вдоль направления растяжения пружины, получаем:

114

Последнее соотношение носит название закона о сохранении механической энергии, который справедлив в случае потенциальных сил.

Рассмотрим пример прямолинейного движения точки массой m из положения 1 в положение 2 на расстояние s под действием постоянных сил, проекцию равнодействующей которых на направление движения обозначим через F. Со- вместная запись теоремы импульсов и теоремы об изменении кине-

Как видно, эти два уравнения содержат шесть неизвестных, по-

этому для определения движения точки необходимо задание четырех параметров. Преобразование предыдущих уравнений приводит к виду v2 − v1 = Ft / m, (v2 − v1)(v2 + v1) = 2Fs / m. Объединяя последние два

уравнения, получим (v2 + v1)t = 2s. Последнее соотношение показы-

вает, что параметры v1, v2, t, s связаны между собой, поэтому для определение закона движения обязательно задавать либо m, либо F.

§ 8. Прямолинейные колебания точки

Рассмотрим точку М, движущуюся прямолинейно под действием только одной восстанавливающей силы F , направленной к непод-

115

вижному центру О и пропорциональной расстоянию от этого центра. Проекция силы F на ось Ох будет:

Fx = −cx .

Найдем закон движения точки М. Дифференциальное уравнение движения будет иметь вид:

Уравнение (9.12) представляет собой дифференциальное урав-

нение свободных колебаний при отсутствии сопротивления.

Это линейное однородное дифференциальное уравнение второго

Величина k называется частотой колебаний. Периодом колеба- ний будет являться величина T=2π/k, так как k(t + 2π/k)=kt + 2π.

Вводя новые постоянные интегрирования по формулам С1=Аcosφ, С2=Аsinφ и используя формулу синуса суммы двух аргу- ментов, получаем:

φ – начальной фазой колебаний.

Часто в реальных условиях на точку, помимо восстанавливающей силы, действует еще и сила сопротивления, направленная в сторону, противоположную движению точки. В случае малых скоростей силу

сопротивления воздуха считают пропорциональным первой степени скорости ее движения: R = −μv .

Рассмотрим влияние подобного сопротивления на свободные ко- лебания материальной точки.

116

Пусть на точку при ее движении действуют восстанавливающая сила F и сила сопротивления R = μv . Тогда Fx = −cx , R = −μv = −μx& и дифференциальное уравнение движения будет иметь

вид

где c / m = k2 , μ / m = 2n .

Последнее уравнение представляет собой дифференциальное уравнение свободных колебаний при сопротивлении, пропорцио-

нальном скорости. Решение этого уравнения ищут в зависимости от соотношения коэффициентов n и k. Очевидно, что n является число- вой характеристикой восстанавливающей силы, а k – силы сопротив- ления.

Если n < k (случай малого сопротивления) , когда восстанавли- вающая сила гораздо больше силы сопротивления. В этом случае ре- шением уравнения (9.15) будет

x = e−nt (C1 sin(k1t) + C2 cos(k1t)),

где k1 = k2 − n 2 . Отметим, что аналогично формуле (9.14) решение можно представить через амплитуду и начальную фазу:

x = Ae−nt sin(k1t + ϕ) .

Последнее уравнение показывает, что в этом случае наблюдаются

затухающие колебания, т.к. lim x = 0.

t→∞

Если n > k (случай большого сопротивления), тогда сопротив- ление в сравнении с восстанавливающей силой велико. В этом случае решением уравнения (9.15) будет иметь вид:

x = C1e + C2e ,

где r = n2 − k2 .

Если k = n (восстанавливающая сила соразмерна с силой сопро- тивления) . В этом случае решение уравнения (9.15) будет иметь вид:

x= e−nt (C1 + C2 t).

Впоследних двух случаях вместо колебаний наступает так назы-

ваемое апериодическое движение.

Эти случаи хорошо иллюстрируются работой пружины (зату- хающие колебания) и амортизатора (апериодическое движение) в подвеске большинства автомобилей.

117

Рассмотрим важный случай колебаний, возникающих, когда на точку, кроме восстанавливающей силы F, действует еще и периоди- чески изменяющаяся со временем сила Q , проекция которой на ось х

равна

Q = Q0 sin pt .

Эта сила называется возмущающей, а колебания, происходящие под действием такой силы, называют вынужденными. Величина р в последнем равенстве является частотой возмущающей силы. В этом случае дифференциальное уравнение движения будет иметь вид:

Последнее уравнение является дифференциальным уравнением вынужденных колебаний точки при отсутствии сопротивления.

Его решение ищут в виде x = x1 + x 2 , где x1 - общее решение одно- родного уравнения, а х2 - частное решение неоднородного уравнения.

В случае свободных колебаний без сопротивления решение x1

было найдено ранее в виде x1 = C1 sin(kt) + C2 cos(kt) = A sin(kt + ϕ) .

Частное решение неоднородного уравнения (9.16) ищется в виде Bsin(pt). Подставляя частное решение в уравнение (9.16), получим

Постоянные А и φ могут быть найдены из начальных условий. Как следует из формулы (9.17), при p → k величина второго сла-

гаемого стремится к бесконечности, то есть если частота вынуждающей силы стремится к частоте собственных колебаний, то возникает условие резонанса, или неограниченного роста амплитуды колебаний.

Рассмотрим пример движения математического ма- ятника, то есть тяжелой материальной точки, подве- шенной на невесомой нерастяжимой нити длиной L. На

118

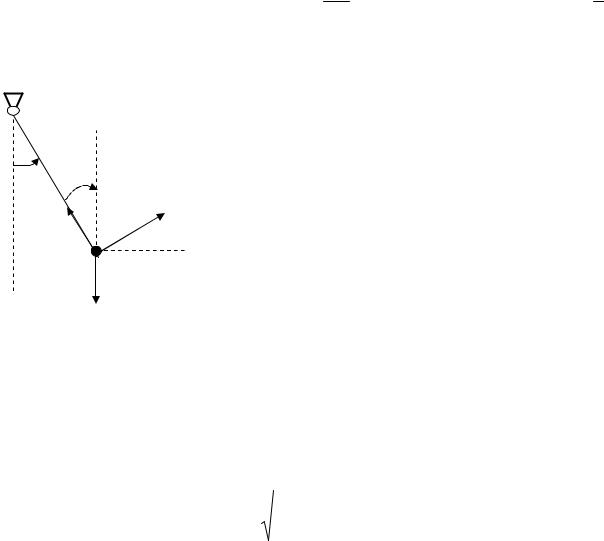
точку действуют сила тяжести mg и сила натяжения нити T

(рис.9.4).

По теореме об изменении количества движения точки имеем

i=1

ведливо в неподвижной системе координат. Однако часто бывает не- обходимо определять характер относительного движения точки, о ко- тором говорилось в главе VIII. Используя теорему Кориолиса (8.4),

i=1

119

Векторы − mапер и − mакор называют соответственно перенос-

ной и кориолисовой силами инерции. Отметим, что силы инерции появляются только в уравнениях относительного движения точки.

Рассмотрим пример движения частицы по лопатке цен- тробежного разбрасывателя (рис.9.5) (вид сверху), пред- ставляющего собой диск, вращающийся с угловой скоростью ω. Указанную лопатку будем принимать за ось х подвижной

системы координат, жестко связанной с диском. В проекции на эту ось на точку действуют следующие силы: сила трения о поверхность диска Fтр2 = fN2, где f – коэффициент трения, N2 = mg – нормальная

родное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение, также как и в параграфе 8, склады- вается из общего решения однородного и частного решения неодно- родного уравнения. Общее решение однородного уравнения имеет

120