
Учебное пособие ТеорМех
.pdf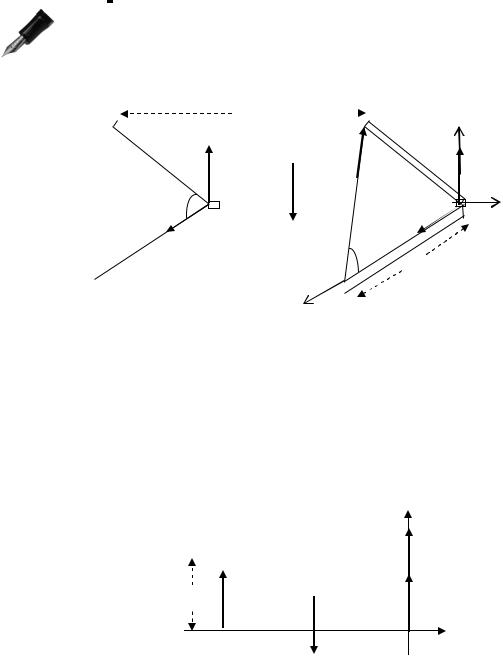
При решении задач на равновесие пространственной системы сил иногда удобно рассмотреть проекции сил на координатные плоскости,
как это показано в следующем примере.
Рассмотрим равновесие верхней части тела, изобра- женного на рис.4.5. Эта часть весом G прикреплена шарни-
рами к нижней части в точках А и В и поддерживается в равновесии стержнем СD. Требуется определить реакции
шарниров и усилие в стержне СD.
|
|
|
|
|
a |
|
|
|
D |
|
z |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
ZA |
G |
T |
|
b |
|
ZB |
||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
XB |
|
B |
||
|
|
XA |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
C |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 4.5 |
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Отметим, что вдоль оси Y сил нет, поэтому и отсутствуют соответствующие реакции связей. Остальные силы показаны на рис.4.5.
Составим три вспомогательных рисунка (4.5.а, 4.5.б и 4.5.в), представляющих собой проекции тела и сил на координатные плос- кости.
|
|
z |
|
|
Tcos(α/2) |
|
|
|
|
ZB |
|
bsinα |
ZA |
||
|
|||
G |
y |
||
|
|
||
|
|
|
Рис 4.5а
Для составления уравнения равновесия вдоль оси Х можно поль- зоваться как рис.4.5б. так и рис.4.5в: XB +XA– Tsin(α/2) =0. Заме- тим, что треугольник CBD равнобедренный, поэтому угол BCD ра- вен углу BDC и равен 90о – α/2. Так как проекций сил на ось Y нет, то нет и соответствующего уравнения равновесия. Для составления
51
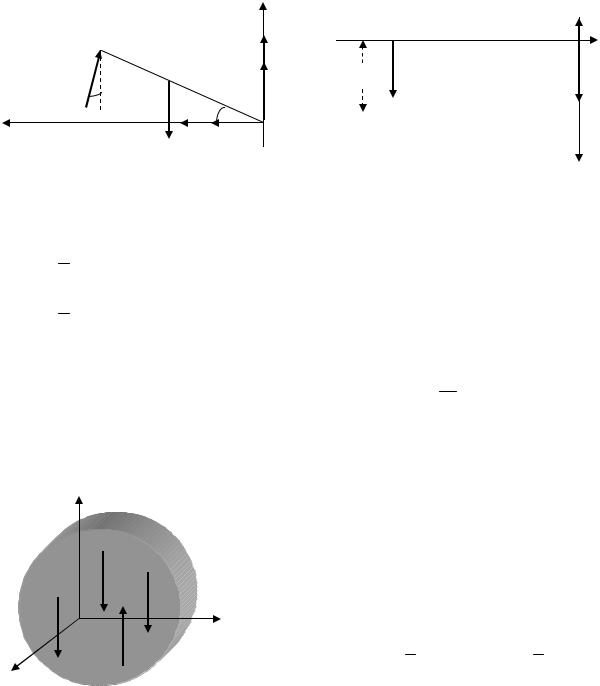
уравнения равновесия вдоль оси Z можно пользоваться как рис.4.5a так и рис.4.5б:
ZB +ZA+ Tcos(α/2)–G =0.
При составлении уравнений моментов относительно осей выби- раются рисунки, на которых соответствующие оси отсутствуют. Так для составления уравнения моментов относительно оси Х выби-
раем
|
|
|
|
z |
|
Tsin(α/2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
ZB |
|
|
y |
|
T |
|
|
bcosα |
XA |
||
|
α/2 G |
|
ZA |
XB |
|||
x |
|
α |
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
XA |
XB |
|
Рис 4.5в |
x |
|
|
|
|
|
|
|
Рис 4.5б
рис.4.5а, относительно оси Y - рис.4.5б,
рис.4.5в:
G × a2 - ZA × a = 0 ,
G × b2 × cos α - T × cos(α / 2) × b = 0,
XA × a = 0 . Из этих уравнений получаем,
T = |
G cos α |
, |
XB = |
G cos α × tg(α / 2) |
|
2cos(α / 2) |
2 |
||||
|
|
|
относительно оси Z -
что XA =0, ZA =G/2, , ZB = G2 (1- cos α).
§6. Случай параллельных сил
|
|
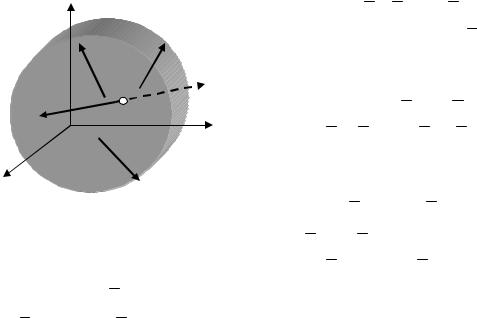
В случае, когда все действующие |
Z |
|
на тело силы параллельны друг другу, |
|
|
можно выбрать координатные оси так, |
|
|
что ось z будет параллельны (рис. 4.6). |
F1 |
|
Тогда проекции каждой из сил на оси х |
Fn |
Y |
и у и их моменты относительно оси z |
|
будут равны нулю, и система (4.1) даст |
|
|
|
X |
F2 F3 |
три условия равновесия: |
||
åFkZ = 0, åmx |
(Fk ) = 0, åmY (Fk ) = 0 |
|||
|
||||
|
|
|||
|
Рис. 4.6 |
Остальные |
равенства обратятся |
|
|
при этом в тождества вида 0=0. |
|||
|
|
|||
52
Следовательно, для равновесия пространственной системы
параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.
§7. Теорема Вариньона о моменте равнодействующей относительно оси
|
Z |
|
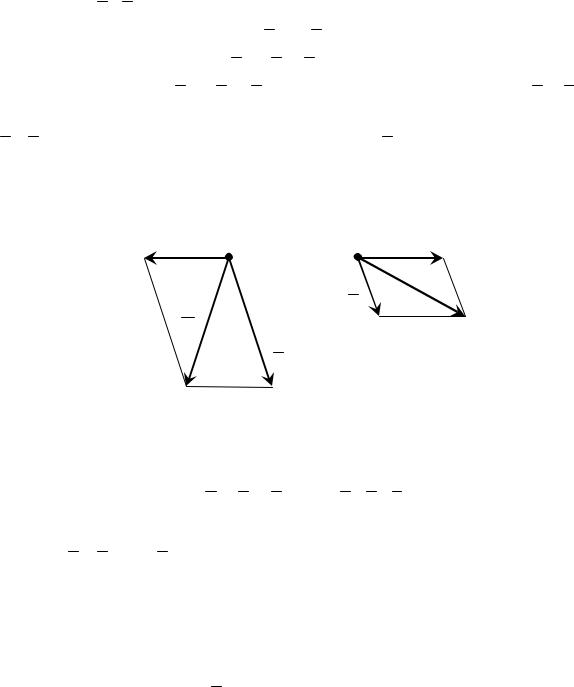
Пусть на твердое тело действует |
||||
|
|
система сил F1 , F2 ,…, Fn , приводящая- |
|||||
|
|
|
ся к равнодействующей R , линия дей- |
||||
|
F1 F2 |
R |
ствия которой проходит через некото- |
||||
|
рую |
точку |
С (рис.4.7). Приложим в |
||||
|
R' |
|
|||||
|
Y |
этой точке силу R |
' |
= −R . Тогда систе- |
|||
|
C |
|
|||||
|
|
|
ма сил F , |
F ,…, |
|
F , R' будет нахо- |
|
|
Fn |
|
|
1 |
2 |
|
n |
X |
|
диться в равновесии и для любой ко- |
|||||
|
|
||||||
|
|
|
ординатной оси Ох будет: |
||||
|
Рис. 4.7 |
|
|
åmx (Fk ) + mx (R' ) = 0. Но так как |
|||
|
|
|
сила |
R' = −R и обе они направлены |
|||
вдоль одной и той же прямой, то mx (R' ) = −mx (R) . Подставляя это значение mx (R' ) в предыдущее равенство, найдем из него, что
mx (R) = åmx (Fk ).
Следовательно, если данная система сил имеет равнодействую- щую, то момент этой равнодействующей относительно любой оси ра-
вен алгебраической сумме моментов слагаемых сил относительно той же оси (теорема Вариньона).
Вопросы для самопроверки
1.Что такое произвольная система сил?
2.Как определяется вектор момента силы относительно центра?
3.Как найти момент пары сил как вектор?
4.Чему равен момент силы относительно оси?
5.Приведите порядок определения момента силы относительно оси.
6.В каком случае момент силы относительно оси считают по- ложительным?
53
ГЛАВА V. ЦЕНТР ТЯЖЕСТИ
§1. Равнодействующая и центр системы параллельных и одинаково направленных сил
Убедимся в том, что система из двух параллельных и одинако- во направленных сил (рис 5.1) имеет равнодействующую, парал- лельную этим силам.
Пусть F1 || F2 . Если в точке А и В приложения сил добавить уравновешенную систему сил P1 = −P2 , а затем силы, приложенные в точке А, заменить одной R1 = F1 + P1 , а силы, приложенные в точке В, заменить силой R2 = F2 + P2 , система параллельных сил F1 , F2
окажется замененной эквивалентной системой сходящихся сил R1,R2 , которая имеет равнодействующую R , являющуюся также равнодействующей данной системы.
|
|
|
|
|
|
|
|
|
|
P1 |
А |
В |
|
|
|
|
2 |
||
|
|
|
|
|
P |
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
R |
||||
F2
R1
F1
Рис. 5.1
По теореме Вариньона, равнодействующая системы равна век- торной сумме данных сил, т. е.
R = F1 + F2 , т. е. R || F1 || F2 .
Рассмотрим систему n параллельных и одинаково направлен- ных силF1, F2 , L , Fn (рис. 5.2). Поскольку две параллельные и оди-
наково направленные силы имеют равнодействующую, очевидно, данная система также имеет равнодействующую.
Введем в рассмотрение единичный вектор e , параллельный данным силам, тогда
Fk = Fk e (k = 1, 2, … n).
По теореме Вариньона равнодействующая системы
54

R = å Fk = å Fk e = (å Fk )e ,
Z
F1 АК F2
FK СК
rК
rC R
 Y
Y
e
X
Рис. 5.2
т. е. равнодействующая параллельна данным силам и имеет модуль, равный сумме модулей данных сил.
Найдем радиус–вектор rc точки С приложения равнодейст- вующей. По теореме Вариньона
mO (R) = å mO (Fk ), или rc ´ R = å rk ´ Fk , или
( rc ´(å Fk ))e = (å rk ´ Fk )e
(здесь rk – радиус-вектор точки приложения силы Fk , k = 1, 2, … n).
Приравнивая в последнем равенстве коэффициенты при векто- ре е , получаем, что
r |
(å F ) = å |
r |
F , откуда |
r |
= å Fk |
rk |
. |
|
c k |
k k |
c |
å Fk |
|||||
|
|
|
|
|
|
|||
Из полученной формулы видно, что положение точки С не за- висит от направления данных сил. Эта точка называется центром параллельных сил.
Поскольку проекции радиуса-вектора на оси х, у, z равны ко- ординатам его конца, то из формулы для rc получаются следующие формулы для координат радиуса-вектора:
55

xc = |
å Fk xk |
; |
yc = |
å Fk yk |
; |
zc = |
å Fk zk |
|
|
å Fk |
|||||
|
å Fk |
|
å Fk |
|
|||
(здесь хk, yk, zk – координаты точки приложения силы Fk ).
§2. Центр тяжести тела
На каждую частицу тела, находящегося вблизи земной поверх- ности, действует направленная вертикально вниз сила тяжести. Для тел, размеры которых малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллель-
ными и сохраняющими постоянное значение при любых поворотах тела.
Z
C 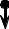 Pk
Pk
P1  rC
rC
P |
Pn |
Y |
X
Рис. 5.3
Равнодействующая P сил тяжести P1 , P2 , … Pn , действующих
на частицы тела, называется весом тела, а центр параллельных сил тяжести С называется центром тяжести тела (рис. 5.3). Модуль си-
лы тяжести: P = åPk ,
радиус-вектор центра тяжести: rC = årkPk , P
координаты центра тяжести: xC = |
åPk xk |
; yC = |
åPk yk |
; |
|
P |
P |
||||
|
|
|
56

zC = åPkzk . P
Благодаря свойству центра параллельных сил не зависеть от направления сил, центр тяжести сохраняет свое положение в теле при любом положении тела в пространстве.
§3. Центр тяжести объема
Для однородного тела вес любой его части пропорционален объему: Pk = γ vk Pk = γΔvk , Р = γV, где vk – объем частицы веса Pk, V – объем всего тела, γ – вес единицы объема.
Подставив эти значения в формулы для координат центра тя- жести, получим
xC = |
åPk xk |
= |
åγ vk xk |
= |
γå vk xk |
= |
å vk xk |
; |
||||
P |
|
|
γV |
|
|
γV |
V |
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
yC |
= |
åvk yk |
; zC = |
åvkzk |
. |
|
|
|||
|
|
V |
V |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Как видно, положение центра тяжести зависит только от гео- метрической формы тела, а от материала тела не зависит. Поэтому центр тяжести однородного тела называют центром тяжести объе- ма.
Если форма тела описывается математически, то в последних равенствах переходят к пределу при числе разбиений, стремящему- ся к бесконечности и vk → 0. В этом случае стоящие в числителях
суммы обращаются в интегралы, распространенные на весь объем тела, и формулы для вычисления координат центра тяжести объема принимают вид:
xC = V1 òV xdV , yC = V1 òV ydV, zC = V1 òV zdV .
§4. Центр тяжести плоской фигуры
Пусть тело представляет собой однородную тонкую пластинку. Обозначим F – площадь фигуры, ограничивающей пластинку (рис. 5.4). Вес однородной пластинки выразится формулой: P = γF, где γ
57

– вес единицы площади, а вес частицы Pk = γΔFk , где Fk - площадь
рассматриваемой частицы. Подставляя эти величины в формулы для координат центра тяжести, получаем:
xC = |
åPk xk |
= |
åγ Fk xk |
= |
å Fk xk |
; |
|
P |
γF |
F |
|||||
|
|
|
|
yC = åFk yk , F
где суммирования распространены на все элементы площади.
y
yk |
|
|
yC |
C |
Pk |
|
xC |
xk |
x |
Рис. 5.4
ют центром тяжести плоской фигуры.
В пределе при Fk → 0
формулы для определения координат центра тяжести однородной пластинки принимают вид:
xC = 1F òF xdF;
yC = F1 òF ydF.
Центр тяжести одно- родной пластинки называ-
Сумма произведений элементарных площадок на алгебраиче-
ские значения их расстояний до некоторой оси называется статиче-
ским моментом фигуры относительно этой оси.
Обозначая Sx и Sy статические моменты плоской фигуры отно- сительно осей х и у, имеем
Sx = òydF, |
Sy = òxdF |
Из формул для координат центра тяжести плоской фигуры на- ходим:
Sx = FxC ; |
Sy = FyC |
Статические моменты выражаются в см3, м3 и т. д. Очевидно,
что статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси.
58
Относительно любой оси, проходящей через центр тяжести се- чения, статический момент равен нулю.
§5. Центр тяжести линии
Определим положение центров тяжести однородных тел, имеющих большую протяженность при сравнительно малой пло- щади поперечного сечения, например, кусок однородной проволоки постоянного сечения, ось которой расположена по дуге кривой АВ
(рис. 5.5).
Вес проволоки P = γL , где L = AB, а γ – вес единицы длины проволоки. Разобьем проволоку на элементарные участки lk . Вес каждого Pk = γΔlk . Подставляя эти величины в формулы для коор- динат центра тяжести тела, получаем:
xC = |
åPk xk |
= |
åγ Lk xk |
= |
γå |
Lk xk |
|
= |
å |
Lk xk |
; |
||||||||||
P |
|
|
|
γL |
|
|
|
γL |
|
|
L |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
yC |
= |
åLk yk |
; zC = |
åLkzk |
|
|
|
||||||||||
|
|
|
|
|
|
L |
|
|
L |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или xC = |
1 |
|
xdL; |
|
|
yC = |
|
1 |
|
ydL; |
|
|
zC = |
1 |
|
zdL |
|
||||
L |
|
|
|
L |
|
|
|
|
|
|
|||||||||||
|
òL |
|
|
|
|
|
òL |
|
|
|
|
L òL |
|
|
|||||||
Центр тяжести такого протяженного тела называют центром тя- жести линии.
z A
lk
B
Pk yk
xk |
y |
|
zk |
||
|
x
Рис. 5.5
59

§6. Способы определения координат центров тяжести тел
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в этой плоскости, на этой оси или в этом центре.
Допустим, например, что однородное тело имеет плоскость симметрии. Тогда этой плоскостью оно разбивается на две такие части, вес которых Р1 и Р2 равны, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Точка приложе-
ния их равнодействующей лежит на равных расстояниях от линий действия P1 и P2 , т.е. в плоскости симметрии. Аналогичный резуль-
тат получается и в случаях, когда тело имеет ось или центр симмет- рии.
Из свойств симметрии следует, что центр тяжести однородного круглого кольца, круглой или прямоугольной пластины, прямо- угольного параллелепипеда, шара лежит в геометрическом центре (центре симметрии).
Точно так же центры тяжести швеллера (рис. 5.6а) и равнопо- лочного уголка (рис. 5.6б) лежат на их оси симметрии (х–х), а центр тяжести двутавра (рис. 5.6 в) лежит на пересечении его осей сим- метрии (х–х и у–у)
|
|
|
|
y |
|
|
|
|
x |
|
|
x |
C |
x |
x |
C |
x |
|
|
|
C |
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
а |
|
б |
|
в |
Рис. 5.6
2. Разбиение. Если тело можно разбить на конечное число та- ких частей, для каждой из которых положение центра тяжести из-
60
