
Учебное пособие ТеорМех
.pdf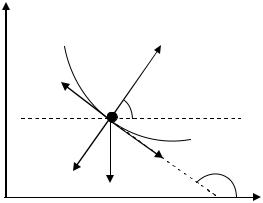
|
|
Для определения |
С1 и |
С2 используем начальные условия: |
||
x |
|
t =0 = x0 , vотн |
|
t =0 = 0 . |
Здесь х0 |
– начальное положение точки на ло- |
|
|
|||||
|
|
|
||||
патке, а равенство нулю начальной относительной скорости спра- ведливо в случае вертикального попадания точки на диск.
Подставляя эти начальные условия в уравнения (9.21) и (9.22), получаем:
x |
0 |
= C + C |
2 |
+ |
fg |
, 0 = C k |
1 |
+ C |
k |
2 |
, откуда |
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
ω2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
æ |
|
|
|
fg ö |
|
|
|
|
|
æ |
|
|
fg |
ö |
|
|||
|
|
|
|
|
|
|
- k |
|
|
- |
|
|
|
|
|
|
- |
|
||||||||
|
|
|
|
|
|
|
|
ç x |
|
|
÷ |
|
|
|
|
|
k |
ç x |
|
|
÷ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
||||||||||||
|
|
|
|
C = |
|
|
2 |
è |
0 |
|
|
ω2 ø |
, C |
2 |
= |
1 |
è |
0 |
|
ø |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
k1 - k2 |
|
|
|
|
|
|
|
k1 |
- k2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставляя в уравнение (9.21) вместо х длину лопатки R, можно определить время движения по ней до момента схода с диска, а из формулы (9.22) – скорость схода частицы с диска.
§ 10. Движение точки по плоской кривой
y |
|
|
|
|
|
Рассмотрим |
|
движение точки |
|||
|
|
|
по некоторой гладкой кривой: |
||||||||
y=f(x) |
|
N |
|
y=f(x) под действием силы тяжести |
|||||||
|
|
|
|
(рис 9.6). Отметим, что на точку |
|||||||
Fтр |
|
|
|
при движении действуют три ак- |
|||||||
α |
|
|
тивные силы: сила тяжести mg, нор- |
||||||||
|
|
|
|
мальная реакция |
|
и сила трения |
|||||
mv2 |
|
|
|
N |
|||||||
|
|
|
|
|
|
|
, где k – коэффициент тре- |
||||
|
v |
|
|
F |
= kN |
||||||
ρ |
|
β |
|
тр |
|
|
|
||||
mg |
|
ния. |
|
|
|
||||||
|
x |
|
|
|
|||||||
|
|
|
|
|
|
Тогда уравнение движения |
|||||
Рис. 9.6 |
|
|
точки в проекции на ось х имеет |
||||||||
|
|
|
|
вид: |
|
|
|
||||
или |
|
|
m&x& = N cos α − Fтр sin α , |
(9.23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m&x& = N(cosα − k sin α), |
(9.24) |
|||||||
Нормальная реакция N определяется условием равновесия сил |
|||||||||||
вдоль оси, |
|
направленной |
по нормали |
к поверхности: |
|||||||
121
N = mg sin α + mvρ 2 , где ρ – радиус кривизны в данной точке. Послед-
нее слагаемое в формуле для определения нормальной реакции явля- ется центробежной силой, с которой точка действует на направляю- щую кривую.
В одном из разделов высшей математики – дифференциальной геометрии – выводится формула для определения радиуса кривизны:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
[1+ (y¢x )2 ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
ρ = |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.25) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y¢x¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вспоминая школьные тригонометрические формулы: |
|
|
|||||||||||||||||||||||||||||||||||||||||||
cos α = |
|
ctgα |
, sin α = |
|
1 |
|
|
|
|
|
|
и |
учитывая, |
|
что |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1+ ctg2α |
|
|
1+ ctg2α |
|
|
|||||||||||||||||||||||||||||||||||||||
tgβ = y¢x = -tg(π - α) = -ctgα , откуда ctgα = −y′x , получаем: |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
− y′x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
cos α = |
|
|
|
|
|
|
, |
sin α = |
|
|
|
|
|
|
. |
|
|
|
|
|
|
(9.26) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1+ (y¢x )2 |
1+ (y¢x )2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Отметим также, что |
|
|
|
|
|
|
æ dy ö2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ dy |
|
|
dx |
ö |
|
+ (y¢x × x& )2 |
|||||||||||||||||
v2 = v2x + v2 y = x& |
2 + y& 2 = x& 2 |
+ |
ç |
|
|
|
÷ |
|
|
= x& 2 |
+ ç |
|
|
|
|
|
× |
|
|
|
÷ |
= x& 2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è dt ø |
|
|
|
|
è dx |
|
|
ø |
|
|
|
||||||||||||||||
и, окончательно, |
|
v2 = x& 2[1+ (y¢x )2 ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Тогда уравнение (9.24) примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
&x& = (g sin α + v2 )(cosα - k sin α) , или |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
& 2 |
¢¢ |
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
yx |
|
|
|
|
|
|
|
|
|
|
|
- yx |
|
|
|
|
|
|
|
|
|
|
|
|
). |
||||||||||
&x& = (g |
|
|
|
+ |
|
|
|
)( |
|
|
|
- k |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1+ (y¢x )2 |
1+ (y¢x )2 |
1+ (y¢x )2 |
1+ (y¢x )2 |
||||||||||||||||||||||||||||||||||||||||||
После очевидных упрощений, получаем:
&x& = - (g + x& 2+y¢x¢ )(k¢ 2+ y¢x ) . (9.27) 1 (yx )
Добавляя к полученному уравнению начальные условия вида:
x t = 0 = x0 , x& t =0 = vx0 ,
получаем задачу Коши для квазилинейного дифференциального уравнения (9.27), которое имеет только численное решение. Напом- ним, что не являющееся линейным дифференциальное уравнение
122
y |
|
|
называется квазилинейным, если его |
||||||||||||
|
|
старшую производную можно выразить |
|||||||||||||
|
|
|
|
|
через младшие. В противном случае |
||||||||||
|
|
|
|
|
уравнение нелинейно. |
|
|||||||||
|
x |
|
|
|
|
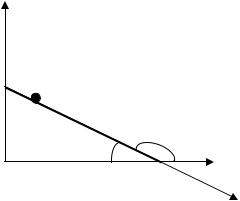
Рассмотрим частный случай дви- |
|||||||||
|
|
|
|
|
жения |
|
по |
наклонной |
плоскости |
||||||
|
z |
|
|
|
|
||||||||||
|
|
β |
|
(рис.9.7). |
|
|
В |
этом |
случае |
||||||
|
ϕ |
|
x |
|
|
||||||||||
|
|
|
tgβ = y′x |
= −tgϕ, |
|
y′x′ = 0 . Учитывая, что |
|||||||||
|
|
|
|
|
|
||||||||||
|
Рис. 9.7 |
|
z |
1+ tg2ϕ = |
|
1 |
|
|
, уравнение (9.27) при- |
||||||
|
|
|
cos2 |
ϕ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
мет вид: |
= −g(k − tgϕ) cos |
2 |
ϕ = g(sin ϕ − k cos ϕ) cos |
ϕ. |
|||||||||||
&& |
|||||||||||||||
|
|
x |
|
||||||||||||
Так как x = z cos ϕ , то x = z cos ϕ, откуда |
|
|
|
||||||||||||
|
|
|
|
&& |
&& |
|
|
|
|
|
|
|
|
|
(9.28) |
|
|
|
|
z = g(sin ϕ − k cos ϕ). |
|||||||||||
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
Это и есть дифференциальное уравнение движения точки по наклонной плоскости.
§11. Движение теряющего массу элемента по прямолинейной плоской поверхности
Название этого параграфа выбрано не случайно. В процессе сель- скохозяйственного производства часто встречают процессы сепара- ции сыпучих сред, смысл которых состоит в удалении ненужных примесей из очищаемого продукта. Это нередко выполняется посред- ством движения некоторого потока по решетам с различного вида от- верстиями, подобранными так, что ненужные примеси естественным образом удаляются из сепарируемой смеси.
В этом случае масса элемента смеси представляет некоторую функциональную зависимость, поэтому, используя свойство произ- водной произведения двух функций, уравнение (9.1) можно записать в виде:
|
dv |
|
dm |
n |
|
|||
m |
+ v |
= å |
|
|
(9.29) |
|||
Fi . |
||||||||
dt |
dt |
|||||||
|
|
i=1 |
|
|||||
В случае сепарации на прямолинейно наклонно расположенных решетах, последнее уравнение принимает вид:
123

m dv |
n |
|
|
= åFi - v dm |
. Здесь v–скорость элемента массы вдоль оси |
||
dt |
i=1 |
dt |
|
z. Учитывая, что согласно уравнению (9.28), сумма активных сил рав-
на
g(sin ϕ − k cos ϕ) , получаем |
(9.30) |
m&z& = mg(sin ϕ − k cos ϕ) − vm. |
|
& |
|
Отметим, что при данном типе сепарации примеси удаляются в направлении, перпендикулярном движению элемента массы, поэтому их относительная скорость в проекции на указанное направление рав- на нулю.
В указанном процессе элемент массы можно вычислять по фор- муле: m = M + mпрe−λz . Здесь M – неизменяемая масса, mпр – началь-
ная масса засорителя, λ – коэффициент сепарации. Отметим, что по- теря массы зависит от длины участка сепарирования.
Найдем производную по времени от массы элемента: |
|
|||||||||||
m& = |
dm |
= |
dm |
|
dz |
|
= -λmпрe−λz × z& . |
|
||||
dt |
dz dt |
|
||||||||||
Учитывая, что v = z и подставляя последнее выражение в (9.29), |
||||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
m&z& = mg(sin ϕ - k cos ϕ) + λmпрe−λz × z&2 . |
|
|||||||||||
Разделив на m , получаем: |
|
|
−λz |
|
|
|
||||||
|
|
|
|
|
|
|
|
λmпрe |
&2 |
|
|
|
&& |
|
|
|
|
|
|
|
|
× z |
|
|
|
|
|
|
|
|
|
+ M + mпрe−λz . |
|
|||||
z = g(sin ϕ - k cos ϕ) |
(9.31) |
|||||||||||
Обычно засоренность определяют отношением массы за-
сорителей к массе чистой фракции p = mMпр , поэтому уравнение
(9.31) окончательно примет вид:
&& |
&2 |
λpe−λz |
|
|
z |
= g(sin ϕ - k cos ϕ) + z |
|
. |
(9.32) |
1+ pe−λz |
||||
Это также квазилинейное дифференциальное уравнение.
124
§ 12. Движение точки в поле силы тяжести с учетом сопротивления воздуха
Вбольшинстве прикладных задач механики аналитическое ре- шение задач движения невозможно. Как было показано в предыдущих параграфах, это касается случаев, когда полученные дифференциаль- ные уравнения квазилинейны или нелинейны.
Вкачестве еще одной задачи, приводящейся к решению квази- линейной системы уравнений, рассмотрим плоское движение частицы
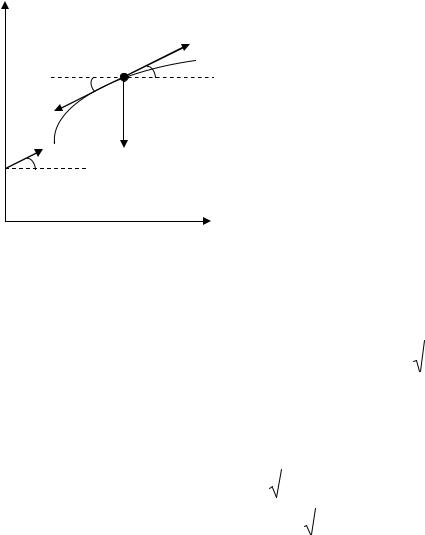
вполе силы с учетом сопротивления воздуха. На частицу М массой m, движущейся по траектории L с текущей скоростью v, действуют
|
|
|
|
|
|
сила тяжести |
mg |
и сила сопротивления |
||||||||||||
y |
|
|
|
|
|
воздуха |
|
|
= mkv2τ , |
|
направленная |
по |
||||||||
|
|
|
|
|
Fc |
|
||||||||||||||
|
|
v |
|
|
|
касательной к траектории L, противо- |
||||||||||||||
|
M |
L |
|
|
|
положно вектору скорости |
|
v (рис.9.8). |
||||||||||||
φ |
|
|
|
|
Постоянная k |
называется коэффициен- |
||||||||||||||
|
φ |
|
|
|
||||||||||||||||
|
|
|
|
том парусности частицы. Этот коэффи- |
||||||||||||||||
Fc |
|
|
|
|
|
|||||||||||||||
mg |
|
|
|
|
циент имеет размерность [1/м ] и зави- |
|||||||||||||||
vo |
|
|
|
|
|
сит только от формы частицы. Диффе- |
||||||||||||||
α |
|
|
|
|
|
ренциальные |
уравнения |
движения |
в |
|||||||||||
|
|
|
|
|
|
|||||||||||||||
h |
|
|
|
|
|
проекциях на оси координат имеют вид: |
||||||||||||||
|
|
|
|
|
|
|
ì |
&& |
|
|
|
2 |
cos |
ϕ |
|
|
||||
|
|
x |
|
|
|
|
ïmx = -mkv |
|
. |
|
||||||||||
Рис. 9.8 |
|
|
|
|
í |
&& |
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
ï |
= -mg - mkv |
sin ϕ |
|
||||||||||||
|
|
|
|
|
|
|
î my |
|
|
|
||||||||||
Учитывая, что cos ϕ = |
v |
x |
, a sin ϕ = |
vy |
, после сокращения на мас- |
|||||||||||||||
|
|
v |
||||||||||||||||||
|
ìx = -kvx v |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
су получаем |
|
|
|
. Учитывая, что v = |
v2x + v2y , |
|
|
|||||||||||||
í && |
= -g - kvy v |
|
|
|||||||||||||||||
|
î y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
vx = x&, vy = y& , окончательно получаем систему уравнений, описы-
вающих рассматриваемое движение
ì&& |
|
|
|
|
|
|
|
& |
& 2 |
& 2 |
|
|
|
||
ïx |
= -kx |
x |
+ y |
. |
(9.33) |
||
í |
|
|
|
|
|
||
ï &y& = -g - ky& |
|
x& 2 + y& 2 |
|
|
|||
î |
|
|
|
|
|
|
|
Добавив к этой системе начальные условия:
При t=0 x = 0, x& = v0 cos α, y = h, y& = v0 sin α , получим задачу для
определения закона движения частицы. В силу квазилинейности сис- темы (9.32), ее решение возможно только численными методами. От-
125
метим, что решение данной системы позволяет определять характер движения частиц с различными коэффициентами парусности. Данная задача возникает, например, при воздушной сепарации потока с раз- личными фракционными составляющими.
Вопросы для самопроверки
1.Сформулируйте законы и задачи динамики точки.
2.Что называют количеством движения точки?
3.Что такое импульс cилы?
4.Сформулируйте общие теоремы динамики точки.
5.Запишите дифференциальное уравнение свободных колебаний без сопротивления среды.
6.Запишите дифференциальное уравнение свободных колебаний при наличии сопротивления среды.
7.Почему при выводе уравнений движении по плоской кривой достаточно одной координаты?
8.Как изменяется движение частицы в случае потери ее массы?
9.В чем разница между уравнениями полета точки с учетом и без учета силы сопротивления?
126
ГЛАВА Х ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
§ 1. Механическая система. Силы внешние и внутренние.
Системой материальных точек (или механической системой) на- зывают такую совокупность, в которой положение или движение ка- ждой точки зависит от положения и движения всех остальных.
Все действующие на систему активные силы и реакции связей разделяют на внешние и внутренние. Внешними ( Fke ) называют силы, действующие на точки данной системы со стороны точек или тел, не входящих в эту систему. Внутренними ( Fki ) называют силы, с кото- рыми материальные точки системы взаимодействуют друг с другом.
На основании закона равенства дей- |
|
|
|
|
|
|
|
||
ствия и противодействия каждой внут- |
|
|
|
|
|
|
|
||
ренней силе соответствует другая внут- |
|
|
|
|
|
|
|
||
|
|
|
F21 |
|
А2 |
||||
ренняя сила, равная ей по модулю и про- |
|
|
|
|
|||||
|
F12 |
|
|
||||||
тивоположная по направлению. Из этого |
А1 |
h |
|
|
|||||
|
|
|
|
||||||
следуют свойства внутренних сил: |
|
|
|
|
|||||
|
|
|
О |
|
|
||||
1. |
Геометрическая сумма всех |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
внутренних сил системы равняется |
|
|
|
|
|
|
|
||
нулю: |
å |
Fki = 0. |
|
|
Рис. 10.1 |
|
|
||
|
|
|
|
|
|
|
|||
2. Сумма моментов всех внутренних сил относительно любого центра или оси равняется нулю (рис.10. 1).
åМо (Fki ) = 0; åМх (Fki ) = 0.
§ 2. Масса системы. Центр масс
Каждая точка системы имеет определенную массу mk , а ее по- ложение относительно системы отсчета Oxyz в каждый момент вре- мени определяется радиус-вектором rk . Масса системы равна ариф- метической сумме масс всех точек или тел, образующих систему: M = åmk . Распределение массы в системе определяется значениями
масс ее точек и их взаимным расположением. Однако оказывается, что при решении большинства задач динамики для учета распределе- ния масс достаточно знать не все величины mk , хк , ук , zк , а выражае-
127
мые через них суммарные характеристики. Ими являются центр масс
иосевые моменты инерции.
Воднородном поле тяжести, для которого g = const, вес любой
частицы тела пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Извест- но, что координаты точек приложения сил тяжести pk , действующих
на частицы тела, определяются так:
x |
= |
åpk x k |
; |
y |
= |
åpk yk |
; |
|
||
åpk |
|
åpk |
|
|||||||
c |
|
|
c |
|
|
|
|
|
||
Учитывая, что |
pk = mk g , получим: |
|
|
|||||||
x |
= |
åmk x k |
; y |
= |
åmk yk |
; |
||||
åmk |
|
åmk |
|
|||||||
c |
|
|
|
c |
|
|
|
|
||
z |
= |
åpk zk |
. |
|
||
|
åpk |
|
||||
c |
|
|
|
|
||
z |
= |
åmk zk |
. (10.1) |
|||
åmk |
||||||
|
c |
|
|
|||
Геометрическая точка С, координаты которой определяются формулами (10.1), называется центром масс механической системы.
Если положение центра масс определять его радиус-вектором, то из равенств (10.1) для rс получается формула:
r |
= |
åmk rk |
, |
(10.2) |
c |
|
åmk |
|
|
где rk - радиус-векторы точек, образующих систему. В случае,
когда твердое тело находится в однородном поле сил тяжести, то его центр масс совпадает с центром тяжести.
§3. Момент инерции тела относительно оси. Радиус инерции
При поступательном движении твердого тела мерой его инертно- сти является масса. При вращательном – момент инерции. Моментом инерции тела или системы относительно данной оси Оz называется скалярная величина, равная сумме произведений масс всех точек тела
или системы на квадрат расстояний от этой оси: Jz = åmk h2k .
Другими словами, осевой момент инерции является мерой инертности тела при вращательном движении. При этом для одной ма-
териальной точки, находящейся на расстоянии h от оси, Jz = mh2 .
Для вычисления осевых моментов инерции можно расстояния от осей выражать через координаты хк , ук , zк этих точек. Тогда моменты инерции относительно осей Oxyz будут определяться формулами:
128
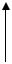
Jx = åmk (yk2 + zk2 ); Jy = åmk (xk2 + zk2 ); |
|
Jz = åmk (yk2 |
(10.3) |
+ xk2 ). |
|
В случае однородного твердого тела, когда количество точек стремиться к бесконечности, а масса точки – к нулю, суммы в фор- мулах (10.3) превращаются в интегралы по соответствующему объе- му:
Jx = ò(y2 + z2 )dm Jy = ò(x2 + z2 )dm |
(10.3а) |
. |
|
Jz = ò(y2 + x2 )dm |
|
Интегралы в формулах (10.3а) следует понимать как интегралы в обобщенном смысле, так как в некоторых ситуациях они могут обра- титься в тройные, двойные и даже в обычные определенные интегра- лы.
В случае однородных тел m = γV , где γ–плотность тела, V–его
объем. Так как dm = γdV , γ = |
|
M |
, где М–масса тела, формулы (10.3а) |
||||||||||||||||||||||||||||||||||||||||||||
|
V |
||||||||||||||||||||||||||||||||||||||||||||||
примут вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Jx |
= |
|
|
|
(y2 |
+ z2 )dV Jy = |
(x2 + z2 )dV |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
V |
ò |
V ò |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(10.3б) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
V ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Jz = |
M |
|
|
|
(y2 + x2 )dV |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Например, момент инерции однородного стержня длиной L отно- |
|||||||||||||||||||||||||||||||||||||||||||||
сительно центральной оси, изображенной |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
на рис. 10.2, равен определенному интегра- |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
лу в промежутке от 0 до L/2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
M |
L / 2 |
|
|
|
|
|
|
M |
æ x3 öL / 2 |
|
|
|
|
|
|
ML2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Jz = |
|
|
|
|
ò x |
2 |
dx = |
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|
Рис. 10.2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
L |
|
|
|
L |
ç |
|
|
÷ |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
− L / 2 |
|
|
|
|
|
|
è |
|
|
3 ø− L / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Момент инерции сплошного однородного диска радиуса R отно- |
|||||||||||||||||||||||||||||||||||||||||||||
сительно центральной |
оси, |
|
|
|
изображенной |
на рис. 10.3, |
равен |
||||||||||||||||||||||||||||||||||||||||
Jz = |
|
|
M |
|
(y2 + x2 )dS = |
|
M |
|
|
|
(y |
2 + x2 )dS = |
|
M |
|
r2 × rdrdϕ = |
|
|
|||||||||||||||||||||||||||||
|
|
S |
ò |
|
|
S |
òò |
|
S òò |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
|
M |
|
2π |
|
R |
|
|
|
|
|
|
|
M |
|
|
|
R4 |
|
|
|
|
|
|
mR2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
òdϕò r3dr = |
|
|
× |
2π = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
S |
0 |
|
0 |
|
|
|
|
|
πR |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
129
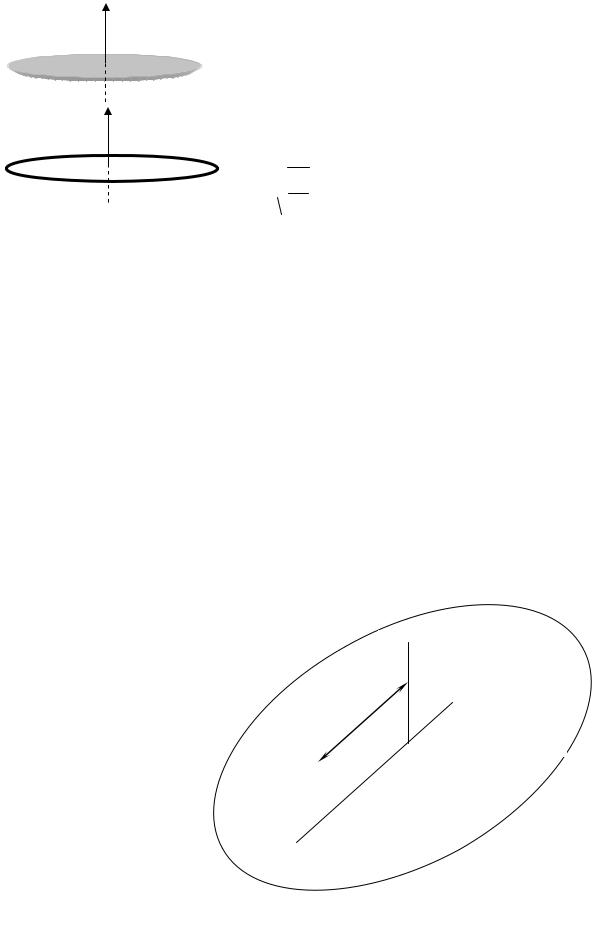
Рис. 10.3
Рис. 10.4
Аналогично вычисляется и момент инерции обода радиуса R относительно центральной оси, изображенной на рис. 10.4
он равен Jz = mR2 .
Часто в ходе расчетов пользуются понятием радиуса инерции. Это линей- ная величина, определяемая равенством:
ρz = 
 MJz , где М – масса тела.
MJz , где М – масса тела.
Радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
Отметим, что радиус инерции имеет размерность [м] и зависит только от формы однородного тела, поэтому в справочной литературе его задание более предпочтительно. Зная радиус инерции и массу со- ответствующего тела, его момент инерции определяется по формуле
Jz = Mρ2z .
§4. Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса
Моменты инер- ции данного тела от- носительно различ- ных осей будут раз- ными. Покажем, как,
зная момент инерции тела относительно одной координатной оси, найти момент инерции относитель- но другой, ей парал- лельной.
Проведем через центр масс С тела произвольные оси
z1
z |
|
d |
C |
|
у1 |
|
|
|
|||||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|
|
|
|
O |
|
у |
|||
|
|
|
|
|
||
x1 x
Рис. 10.5
130
