
Учебное пособие ТеорМех
.pdf
Отличие кинетической энергии от введенных ранее понятий ко-
личества движения системы и кинетического момента заключается в том, что во-первых, она является характеристикой и поступательного и вращательного движения, во-вторых, это величина скалярная и в третьих, на ее изменение влияют как внешние, так и внутренние силы системы.
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
Поступательное движение. В этом случае все точки тела дви- жутся с одинаковыми скоростями, равными скорости центра масс системы. Следовательно, для любой точки vk = vc и из формулы
(10.18)
Tпост = å |
mk vс2 |
= å(mk ) |
vс2 |
= M |
vс2 |
. |
|
|
|
||||
2 |
2 |
2 |
|
|||
Кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости его центра масс.
Вращательное движение. Если тело вращается вокруг какой- нибудь оси Оz (рис.10.11), то скорость любой ее точки определяется как vk = ωhk , где hк – расстояние от точки до оси вращения, ω – угло-
вая скорость тела. Подставляя это значение в формулу (10.17), полу-
чим Tвр = å mk υk2 |
= å mkω2hk2 = å(mk hk2 ) ω2 , |
|
|
|
|
|
||
2 |
2 |
2 |
|
|
|
|
|
|
z |
а учитывая, что å(mk h k2 ) = Jz , окон- |
|||||||
|
чательно получаем |
|
|
|
|
ω2 |
|
|
|
|
|
= |
J |
z |
|
||
ω |
T |
|
|
|
. |
(10.19) |
||
|
|
|
|
|||||
вр |
|
|
2 |
|
|
|||
hk |
Кинетическая |
|
энергия |
тела при |
||||
|
Vk вращательном движении равна полови- |
|||||||
|
не произведения момента инерции тела |
|||||||
|
относительно оси вращения на квадрат |
|||||||
|
его угловой скорости. |
|
|
|
|
|
||
|
Плоское движение. При этом движе- |
|||||||
|
нии скорости всех точек тела в каждый |
|||||||
Рис. 10.11 |
момент времени распределены так, как ес- |
|||||||
|
ли бы тело вращалось вокруг оси, перпен- |
|||||||
дикулярной плоскости движения и проходящей через мгновенный
141
центр скоростей Р (рис.10.1). Следовательно, по формуле (10.18) ки- нетическая энергия тела в каждый момент времени будет определять- ся:
|
|
|
|
|
|
|
|
= |
|
J |
Р |
ω2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(10.19) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
плоск |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
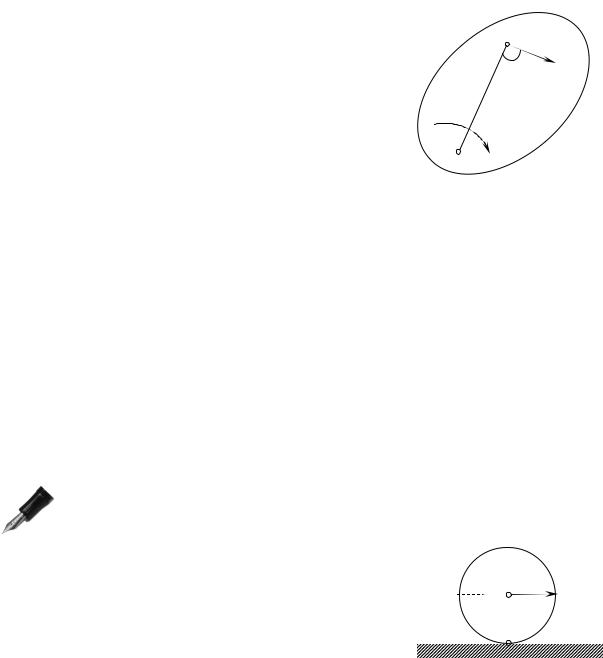
где JР - момент инерции относительно оси, |
|
|
|
|
|
|
|||||||||||||||||||||
проходящей через мгновенный центр скоро- |
|
|
|
С |
|
||||||||||||||||||||||
стей Р. Очевидно, что величина JР |
|
|
является |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
90о |
υс |
|||||||||||||||||||||
мгновенной, т.е. постоянно меняется с тече- |
|
|
|
|
|||||||||||||||||||||||
нием времени. Введем вместо нее постоянный |
|
|
|
|
|
|
|||||||||||||||||||||
момент инерции JС относительно оси, прохо- |
|
|
|
ω |
|
||||||||||||||||||||||
дящей через центр масс С тела. Тогда, по тео- |
|
|
Р |
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
реме Гюйгенса |
JР = JС + Md2 , |
где |
d=РС. |
|
|
|
Рис. 10.12 |
||||||||||||||||||||
Подставив это выражение в (10.20), получим: |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
J |
Р |
ω2 |
|
(J |
С |
+ Md2 )ω2 |
|
J |
С |
ω2 |
+ Md2ω2 |
|
|||||||||||||
T |
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
плоск |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
Учитывая, что точка Р – мгновенный центр скоростей и, следова- |
|||||||||||||||||||||||||||
тельно, ωd = ω× PC = vc , а значит |
|
|
|
|
ω2 |
|
|
Mv2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
= |
J |
С |
+ |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
c |
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
плоск |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
т.е., при плоском движении кинетическая энергия тела равна
энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.
|
|
|
Пример. Определим кинетическую энергию катка массы M и |
|||||||||||||||
|
|
|
радиуса R , движущегося со скоростью vс по горизонтальной |
|||||||||||||||
|
|
|
поверхности (рис.10.13). Тогда его кинетическая энергия оп- |
|||||||||||||||
|
|
|
ределится по формуле: |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
J |
С |
ω2 |
Mv2 |
|
|
|
|
||
|
|
|
|
T |
|
|
= |
|
|
+ |
c |
. |
|
|
|
υс |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
плоск |
|
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|||
|
Учитывая, что момент инерции сплошно- |
|||||||||||||||||
|
|
|||||||||||||||||
го диска JС = |
|
MR 2 |
, получаем: |
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
Рис. 10.13 |
||||||||||||||
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
MR2ω2 |
Mv2 |
|
|
|
|
|
|
|
|
||||||
|
|
= |
+ |
, кроме того, ω = |
v |
c |
|
|
||||||||||
T |
|
|
|
|
|
|
c |
|
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
плоск |
|
2 × 2 |
|
|
|
2 |
|
|
|
|
|
|
R |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
следовательно,
142

T = |
MR2vc2 |
+ |
Mvc2 |
= |
3 |
Mv2 . |
|
|
|
|
|||||
плоск |
2 |
× 2 × R2 |
2 |
|
4 |
c |
|
|
|
|
|||||
§15. Теорема об изменении кинетической энергии системы
Ранее была доказана теорема, справедливая для любой из точек системы. Следовательно, если рассмотреть какую-нибудь точку сис- темы массой mk, имеющую скорость vk, то для этой точки будет
d mk vk2 |
= dAek + dAik , |
2 |
|
где dAek , dAik - элементарные работы действующих на точку
внешних и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, найдем, что
då mk vk2 |
= ådAek + ådAik или |
|
2 |
|
|
dT = ådAek + ådAik . |
(10.21) |
|
Равенство (10.20) выражает теорему об изменении кинетической энергии системы в дифференциальной форме. Проинтегриро-
вав обе части этого равенства в пределах, соответствующих переме- щению системы из некоторого начального положения, где кинетиче- ская энергия равна То, в положение, где значение кинетической энер- гии становится равным Т1, получим
T1 - То = åAek + åAik . |
(10.22) |
Пример. Определим угловую скорость и угловое ускоре- ние стержня массой M и длиной L, движущегося из состоя- ния покоя как это показано на рис.10.14. Так как стержень, находящейся в состоянии покоя, совершает вращательное
движение относительно оси z, проходящей через точку О, то тео-
|
С |
рема об изменении кинетической энергии |
|||||||
О |
|
будет |
выглядеть |
следующим |
образом: |
||||
|
|||||||||
φ |
|||||||||
|
Jzω2 |
|
|
L |
|
|
|
||
|
С |
= Mg |
sin ϕ. |
Здесь работа силы |
|||||
|
2 |
2 |
|||||||
|
|
|
|
|
|
|
|||
|
|
тяжести определяется, в силу ранее |
|||||||
|
ω,ε |
указанной ее потенциальности, |
на вер- |
||||||
|
тикальном перемещении |
L |
|
Рис. 10.14 |
2 sin ϕ . Учиты- |
||
|
|
|
|
143

вая, что Jz = |
ML2 |
, получаем: ML2 ω2 = Mg |
L sin ϕ, откуда |
|||||
|
3 |
3 |
2 |
|
2 |
|||
|
|
ω2 = |
3g |
sin ϕ . |
(10.23) |
|||
|
|
|
|
|||||
|
|
|
|
L |
|
|||
Последнее выражение дает нам искомую угловую скорость: |
||||||||
|
|
|
|
|
|
|
||
|
|
ω = |
3g |
sin ϕ . |
(10.24) |
|||
|
|
|
||||||
|
|
|
|
L |
|
|||
Дифференцируя выражение (10.22) по времени с учетом того, что и ω и φ являются функциями, зависящими от времени, получаем:
& |
3g |
& |
& |
|
& |
|
||
L |
|
|||||||
2ω× ω = |
cos ϕ × ϕ . Так как ϕ = ω, а ω = ε , то |
|
||||||
|
|
|
|
|
ε = |
3g |
cos ϕ. |
(10.25) |
|
|
|
|
|
2L |
|||
|
|
|
|
|
|
|
|
|
Отметим, что при φ=π/2 угловая скорость стержня макси- |
||||||||
мальна, а угловое ускорение равно нулю. |
|
|||||||
|
|
|
|
Рассмотрим пример движения физического маятни- |
||||
|
|
ка, то есть тела, подвешенного в некоторой точке и со- |
||||||
|
|
вершающего |
качание |
относительно этой |
точки |
|||
|
|
(рис.10.15). Запишем уравнение вращения твердого тела: |
||||||
|
|
|
|
|||||
Jzε = åmz (Fk ) = -mg × OC × sin ϕ. По теореме Гюйгенса |
|
|||||||
 O
O
φ
 ω
ω
C
mg
Рис. 10.15
(JС + m × OC2 )ϕ&& = -mg × OC × sin ϕ .
Здесь JC – момент инерции тела отно- сительно оси, проходящей через центр масс С. Вводя в рассмотрение радиус инерции тела относительно централь-
ной оси, получаем JC = mρC2 . Тогда
(mρC2 + m × OC2 )ϕ&& = -mg × OC × sin ϕ.
При малых колебаниях sin ϕ ≈ ϕ , после некоторых преобразований:
&& |
g |
ϕ = 0. Обозначим че- |
|
ρC2 + OC2 |
|||
ϕ + |
|
ρ2 |
+ OC2 |
OC |
|
рез Lпр = |
и назовем эту величину приведенной длиной фи- |
|||
C |
OC |
|||
|
|
|
зического маятника. Окончательно получаем:
144

&& |
g |
ϕ = 0. |
|
Lпр |
|
||
ϕ + |
(10.26) |
Это уравнение абсолютно аналогично уравнению колебаний математического маятника (9.18), приведенного в главе 9. Отсюда следует, что период колебания физического маятника определяется по формуле:
T = 2π |
|
Lпр |
|
. |
(10.27) |
|
|||||
|
|
g |
|
||
Таким образом, колебания данного физического маятника будут происходить по такому же закону, что и колебания математическо- го маятника с длиной нити, равной
Lпр = |
ρ2 |
+ OC2 |
. |
(10.28) |
C |
OC |
|||
|
|
|
|
§16. Экспериментальные определения моментов инерции
В ряде случаев для тел нестандартной формы необходимо экс- периментально определять моменты или радиусы инерции. Для этого можно использовать метод маятниковых колебаний, сущность ко- торого состоит в следующем.
Предварительно определяется центр масс тела C. Затем тело под- вешивается в некоторой точке O, не являющейся центром масс, от- клоняется от положения равновесия на небольшой угол, после чего оно начинает совершать малые колебания. С помощью секундомера с некоторой повторностью опыта определяется период колебаний Т.
Затем тяжелая материальная точка подвешивается на невесомой нерастяжимой нити (математический маятник) и начинает совершать малые колебания. Длина нити Lпр в ходе опытов выбирается так, что- бы период колебаний стал равен Т. После чего из формулы (10.28) определяется искомый радиус инерции:
ρC = 
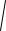 Lпр × OC - OC2 .
Lпр × OC - OC2 .
В некоторых случаях может быть применен метод крутильных колебаний. Он состоит в том, что тело подвешивается в центре масс на упругой проволоке и приводится к малым крутильным колебани- ям. С помощью секундомера с некоторой повторностью опыта опре- деляется период колебаний Т. Используя уравнение вращения твердо-
го тела (10.18): Jzε = åmz (Fk ) и тот факт, что на тело действует только момент сопротивления кручению mz = –cϕ, получаем
145

Jzϕ = −cϕ , или ϕ + |
c |
ϕ = 0 . Аналогично рассматриваемым выше слу- |
|
&& |
&& |
Jz |
|
|
|
|
|
чаям математического и физического маятников, период крутильных колебаний определится по формуле:
T = 2π |
|
Jz |
|
. |
(10.29) |
|
|||||
|
|
c |
|
||
Затем к этой же проволоке подвешивается некоторое эталонное тело, например, сплошной однородный диск, момент инерции которо- го Jэт известен. Также опытным путем определяется период его кру-
тильных колебаний Тэт. Так как T |
= 2π |
|
|
Jэт |
|
, то разделив последнее |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
эт |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
||
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
|||
|
|
|
|
J |
эт |
|
|
|
|
|
|
|
|
|
|
|
|||
равенство на (10.28), получим |
эт |
= |
|
|
|
|
|
, откуда J |
|
= J |
|
|
. |
||||||
T |
|
|
|
|
z |
эт T2 |
|||||||||||||
|
|
|
|
J |
z |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эт |
|
|||
§17. Плоское движение твердого тела
Учитывая рассуждения, приведенные в §14 данной главы, плос- кое движение твердого тела можно рассматривать как плоское дви- жение его центра масс в системе координат (x,y) и вращательное движение вокруг этого центра масс:
|
&& |
= |
åFix |
|
|
|
|
ü |
|
||
mx |
|
|
|
|
ï |
|
|||||
|
&& |
= |
åFiy |
|
|
|
|
ï |
(10.30) |
||
my |
|
|
|
|
ý . |
||||||
J |
|
&& |
å |
m |
|
|
|
|
ï |
|
|
|
|
|
|
|
|
||||||
|
C |
|
|
|
C |
|
i |
þ |
|
||
Рассмотрим |
|
следующий |
|
|
пример. Пусть |
однородный |
|||||
диск катится вверх по наклонной плоскости с углом α, имея начальную скорость центра v0. Коэффициент сопротивле-
ния |
качению равен f. Требуется определить, |
какой путь |
|||
|
|
|
x |
пройдет диск до останов- |
|
|
|
N1 |
ки? |
|
|
|
|
|
направление |
||
|
|
|
|
Выберем |
|
|
C |
|
|
по наклонной плоскости за |
|
|
|
|
|
ось х (рис.10.16). Тогда в |
|
N2 |
mg |
μ |
|
системе (10.30) останется |
|
α |
|
|
первое и третье уравнения. |
||
|
|
|
|||
|
Рис. 10.16 |
|
На диск, кроме силы тяже- |
||
|
|
|
|
||
146
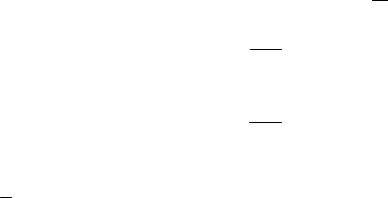
сти mg, действуют еще проекции нормальной реакции N1 и N2 (см. рис.3.19). Запишем уравнения плоского движения диска:
m&x& = −mg sin α − N2 , JCϕ&& = N2R − N1μ . Здесь R – радиус диска, μ
– коэффициент трения качения (см. главу 3). Учитывая, что в на- правлении, перпендикулярном оси х, движение отсутствует, получа- ем:
mg cos α = N1. Тогда |
уравнение вращения |
примет |
вид: |
||||
mR2 |
&& |
|
mR |
&& |
|
μ |
. Как |
2 |
|
2 |
|
|
|||
ϕ = N2R − N1μ , или, после деления на R, |
ϕ = N2 − N1 R |
||||||
и в главе 3, обозначим коэффициент сопротивления качению f = Rμ .
Из последнего уравнения можно выразить N2: N2 = mR2 ϕ&& + fN1 . Под-
ставляя значения проекций нормальной реакции N1 и N2 в уравнение движения вдоль оси х, получаем: m&x& = −mg sin α − mR2 ϕ&& − fmg sin α.
Учитывая, что &x& = Rϕ&& , после сокращения на m и некоторого упро-
щения, получим: &x& = − 23 g(sin α + f sin α) . Если принять, что при t=0
& |
, |
|
|
|
|
|
x=0, x = v0 |
|
|
|
|
|
|
то, после интегрирования последнего уравнения, получаем: |
||||||
|
x& = − |
2 g(sinα + f sinα)t + v0 , |
(10.31) |
|||
|
|
1 |
|
3 |
|
|
|
x = − |
g(sin α + f sin α)t2 |
+ v0t . |
(10.32) |
||
|
|
|||||
|
3 |
|
|
|
||
& |
|
|
|
|
|
Полагая в (10.31) x = 0, получаем время движения по наклонной |
|||||
плоскости до остановки |
t = |
|
3v0 |
, а из(10.32) - пройден- |
|
2g(sin α + f sin α) |
|||||
ный путь |
|
|
3v02 |
|
|
|
x = |
|
. |
||
|
|
|
|||
4g(sin α + f sin α)
147
Вопросы для самопроверки
1.Что называют механической системой?
2.Каковы свойства внутренних сил системы?
3.Чем характеризуется мера инертности тела при поступатель- ном и вращательном движениях?
4.Что такое радиус инерции?
5.Сформулируйте теорему Гюйгенса.
6.Сформулируйте теорему о движении центра масс системы.
7.Сформулируйте теорему об изменении количества движения системы.
8.Что называют кинетическим моментом системы?
9.Как определить кинетическую энергию во вращательном движении?
10.Как определить кинетическую энергию в плоском движении?
11.Сформулируйте теорему об изменении кинетической энергии системы?
148
ГЛАВА XI. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
В различных областях современной техники возникают сложные задачи, для решения которых желательно иметь универсальный ана- литический аппарат, основанный на общих принципах механики. Раз- работка такого аппарата, изложение общих принципов механики, вы-
вод из них дифференциальных уравнений движения и исследование самих уравнений и методов их интегрирования составляют основное содержание аналитической механики.
§ 1. Принцип возможных перемещений.
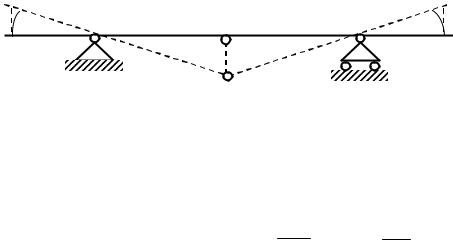
Возможным (или виртуальным) перемещением несвободной ме- ханической системы называется всякое воображаемое бесконечно ма- лое перемещение, допускаемое в данный момент наложенными на систему связями. Из данного определения вытекает, что возможные перемещения точек механической системы рассматриваются как бес- конечно малые первого порядка малости. Так, например, возможным перемещением шарнирного рычага АСВ (рис.11.1)
А’ |
А1 |
B |
1 |
B’ |
δsA |
|
δsB |
||
C |
|
|
||
А |
|
δsC |
|
B |
|
|
|
|
C’
Рис. 11.1
является поворот звеньев АС и СВ в результате бесконечно малого смещения δsс шарнира С в вертикальном направлении. Это смещение вызовет перемещения точек А и В по дугам AA1 и BB1. Однако с точ- ностью до величин первого порядка малости эти перемещения заме-
няют возможными перемещениями δsA = AA' и δsB = BB' , перпенди-
кулярными к АВ.
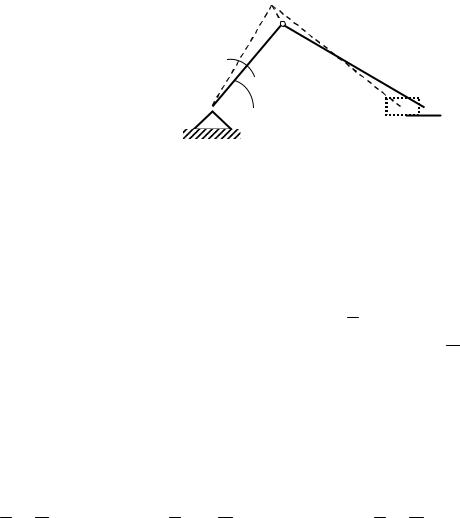
Возможным перемещением кривошипно-ползунного механизма, изображенного на рис.11.2, является поворот кривошипа OA из за- данного положения, определяемого углом φ, на бесконечно малый угол δφ вокруг оси О. Возможное перемещение δsА точки А представ- ляет собой отрезок касательной АА' к дуге АА1, равный по величине δsA = OA × δϕ . Возможным перемещением δsB точки В ползуна явля-
ется бесконечно малый отрезок BB1 прямолинейной траектории точки В.
149
А’ А1 
А
δφ
φ
О

 В1 В
В1 В
Рис. 11.2
Действительные перемещения точек несвободной механической системы, совершаемые от действия приложенных сил, всегда нахо-
дятся среди возможных перемещений точек системы только в том случае, если наложенные на систему связи не изменяются со временем. Такие связи называются стационарными.
Будем рассматривать несвободную механическую систему из n материальных точек. Обозначим через Fi равнодействующую задан- ных активных сил, приложенных к i-й точке, через Ri — равнодейст-
вующую сил реакций связей в этой точке, a δsi — ее возможное пере-
мещение. Связи, для которых сумма работ реакций на любом воз-
можном перемещении системы равна нулю, называются идеаль-
ными. По определению, для систем с идеальными связями
|
|
i ,δsi ) = 0 , (i=1, 2, …, n). |
(11.1) |
åRiδsi cos(R |
|||
Если система находится в равновесии, то для каждой из n точек Fi + Ri = 0, то есть Fi = −Ri . Так как силы Fi и Ri равны по величине и противоположны по направлению, то cos(Fi ,δsi ) = − cos(Ri ,δsi ) и
работы этих сил на возможном перемещении точки δsi, равны по ве- личине, но противоположны по знаку. Поэтому сумма элементарных работ всех сил, приложенных к i-й точке, на любом возможном пере- мещении равна нулю:
Fiδsi cos(Ri ,δsi ) + Riδsi cos(Ri ,δsi ) = 0 , (i = 1, 2,..., n).
Суммируя такие равенства по всем точкам системы, получим:
åFiδsi cos(Ri ,δsi ) + åRiδsi cos(Ri ,δsi ) = 0, (i = 1, 2,..., n).
Отсюда, в случае системы с идеальными связями с учетом усло-
вий (11.1), имеем: |
|
åFiδsi cos(Ri ,δsi ) = 0, (i = 1, 2,..., n). |
(11.2) |
Равенство (11.2) выражает принцип возможных перемещений:
для равновесия механической системы с идеальными стационарными связями необходимо и достаточно обращения в нуль суммы
150
