Учебное пособие ТеорМех

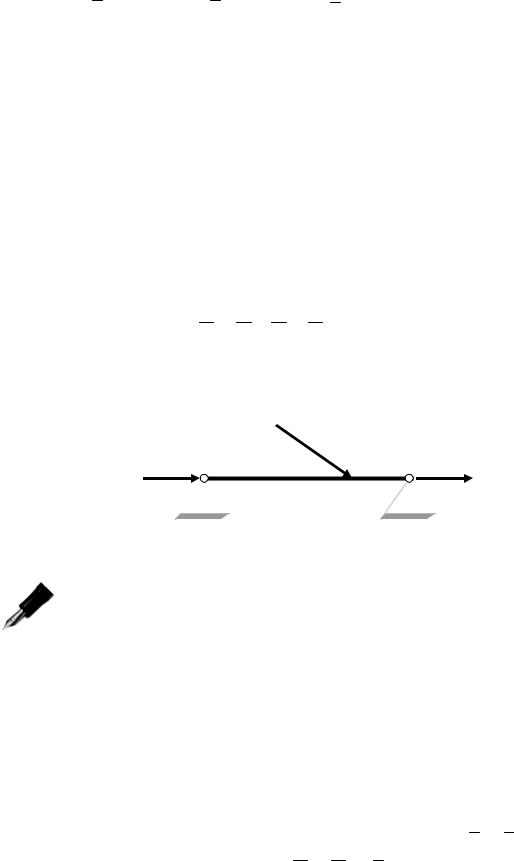
å mA (Fk )= 0; å mB (Fk )= 0;

ной прямой).

Действительно, первые два из предыдущих равенств гарантиру- ют равенство нулю главного момента системы сил, но при этих усло- виях главный вектор может лежать на прямой АВ. Третье же условие обязывает этот вектор быть равным нулю, так как точка С не лежит на прямой АВ.

Очевидно, что при нахождении условий равновесия некоторых тел, находящихся под действием плоской системы сил, в этих уравне- ниях не должно быть более трех неизвестных, иначе система (3.1) бу- дет неразрешима. В этих ситуациях задача становится статически неопределимой. Например, в простейшей ситуации равновесия бал- ки, опирающейся на два неподвижных шарнира (рис.3.8), мы имеем 4 неизвестных силы – XA , YA , XB , YB , что не дает возможности их

определения.

YA F YB

XA A B XB

Рис 3.8

Пример статически определимой задачи нахождения реак- ций опор балки, которая часто встречается в заданиях для студентов, начинающих изучение статики.

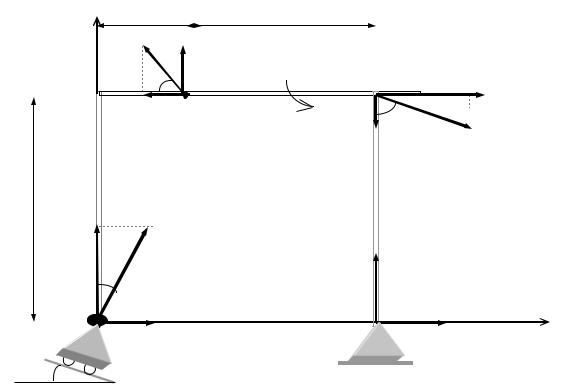
Жесткая рама (рис.3.9) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на

катках. Все действующие силы и размеры показаны на рисунке.

Дано: F1= 25 кН, F 2=18 кН, α =60о , γ =75о , β =30о , М= 50 кН·м, а=0,5 м.

Определить реакции в точках А и В, вызываемые действующими нагрузками.

Решение. Рассмотрим равновесие рамы. Проведем координат- ные оси ХY и изобразим действующие на раму силы F1 , F2 , пару сил с моментом М и реакции связей XA , YA , RB (реакцию неподвижной опоры А изображаем двумя ее составляющими, реакция шарнирной

31

опоры на катках направлена перпендикулярно опорной плоскости).

Для полученной плоской системы сил составим три уравнения

Рис. 3.9

Подставив в составленные уравнения числовые значения задан- ных величин и решив эти уравнения, определим искомые реакции: ХА =-8,5 кН; YА= -23,3 кН; RB= 7,3 кН. Знаки указывают на то, что си- лы ХА и УА направлены противоположно показанным на рис.3.9

§ 5. Условия равновесия составных тел

Иногда возникает необходимость определить условие равнове- сия и (или) реакции опор составных тел, т.е. твердых тел, каким-либо образом соединенных между собой.

Представим себе два тела, шарнирно соединенных между собой в точке С (рис.3.10). На каждое из этих тел могут действовать различ-

32

ствляет воздействия на другое, которые по третьему закону Ньютона должны быть равны между собой, полу- чаем следующую ситуацию (рис.3.11).

Рис. 3.11

Далее, для каждого из тел составляются три уравнения равнове- сия, из которых определяются неиз- вестные силы.

В ситуации, когда тела облокачи- ваются одно на другое без трения, картина аналогична (рис.3.12).

В этом случае тело также “раз- рывается” на две части, и действия

каждой части на другую компенсируется силами реакции связей, рав- ными по величине и противоположными по направлению (рис.3.13 ). Сила реакции RC направлена перпендикулярно плоскости, на кото- рую облокачивается одно из тел.

RC

С

С

RC

Рис. 3.13

Рассмотрим пример, который иллюстрирует тот факт, что

при определении неизвестных усилий в составных телах не обязательно составлять все уравнения равновесия. На

33

рис.3.14 изображено составное тело, состоящее из трех шарнирно соединенных между собой балок, две из которых опираются на не- подвижные шарниры. Требуется определить величину силы F, необ- ходимую, чтобы тело находилось в равновесии, считая величину силы

Q заданной и AK = KC = BP = PD.

Рис. 3.14

Решение. Разъединим наше составное тело в шарнирах С и D и

заменим силы взаимодействия соответствующими реакциями связей

(рис.3.15).

Попробуем составить наименьшее число уравнений, которые могли бы определить неизвестную величину силы F. Первым уравне-

нием рационально составить уравнение моментов относительно точки А:

XC × AC - Qsinα × AK = 0 .

Учитывая, что AC=2AK, получаем, что

XC = 12 Q ×sin α .

Далее, составляя для средней части конструкции уравнение равновесия в направлении оси Х, получаем, что

XD = -XC = - 12 Q ×sin α.

Cоставляя теперь уравнение моментов относительно точки В, мы получаем соотношение: F = - 12 XD = 14 Q ×sin a .

34

YD XC YC YC YD XD

K XC XD P F

Q

XB

XA YB

YA

Рис. 3.15

§ 6. Трение

Трение двух соприкасающихся тел представляет собой довольно сложное физическое явление, сопровождающееся нагревом тел, их электризацией, разрушением, диффузией вещества и многими други- ми явлениями. Интенсивность взаимодействия тел при трении зави- сит от множества обстоятельств, среди которых наибольшее значение

имеют интенсивность сдавливания тел, характеризуемая нормальной составляющей реакции взаимодействия между телами, скорость их взаимного перемещения и степень обработки поверхностей материала трущихся тел.

Первой из сил трения рассмотрим трение покоя. Представим се- бе ситуацию, когда к телу весом G прикладывается горизонтальная сила F (рис.3.16). Если сила F начинает возрастать от своего нулево- го значения, то тело все же будет оставаться в покое. Следовательно, горизонтальная составляющая реакции поверхности, называемая си- лой трения покоя Fтр.п , уравновешивает приложенную силу F и воз-

растает вместе с ней до тех пор, пока равновесие тела не нарушится. Это произойдет в тот момент, когда сила трения покоя не достигнет своего максимального значения, называемого силой трения покоя, которая, как показывают опытные данные, определяется по формуле

Fтр, п = fпN,

где fп – коэффициент трения покоя, N – нормальная реакция поверх- ности.

Часто ошибочно считают, что коэффициент трения покоя обяза- тельно должен быть меньше единицы. Это неверно, так как при дос-

таточно шероховатой или липкой поверхности значение величины силы Fтр, п = F может превышать величину нормальной реакции N .

35

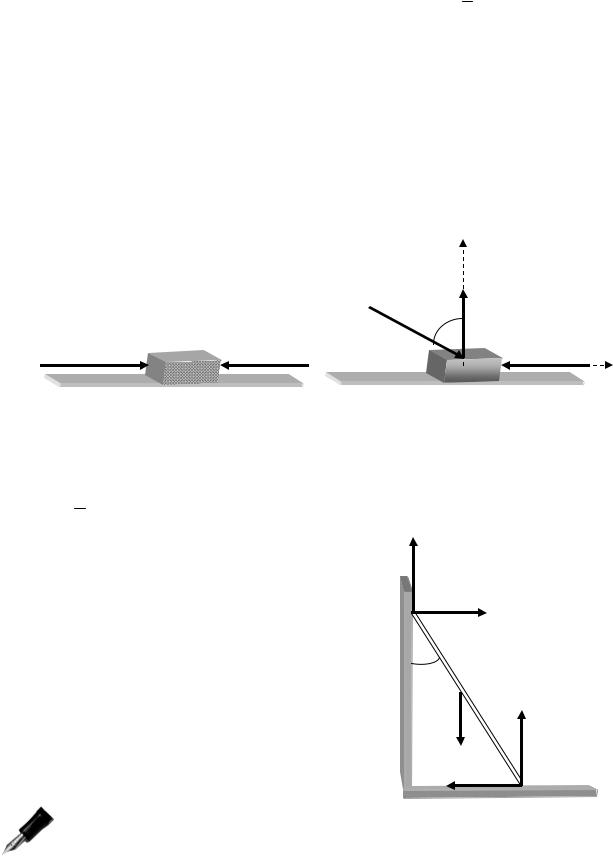
Рассмотрим теперь ситуацию, в которой мы пытаемся вывести тело из положения равновесия с помощью некоторой силы Q, направленной

под углом α к вертикальной оси Y (рис.3.17). Спроектировав дейст- вующие на тело силы на ось Y, получаем следующее соотношение: N - Qcosα = 0. Отсюда N = Qcosα. Проектируя теперь силы на ось X, выводим следующее соотношение Qsinα - fпQcosα = 0, откуда следу-

ет, что fп =tgα.

Таким образом, если сила, действующая на тело, отклонена от вертикали на угол α, меньший arctgfп, то тело будет находиться в рав- новесии независимо от величины этой силы (рис.3.17). Эта область называется конусом трения.

Когда тело выводится из состояния покоя, то при его движении по некоторой поверхности возникает сила трения скольжения, ве- личина которой определяется по формуле такой же, как и сила трения покоя: Fтр = fN , где f – коэффициент

стоянии равновесия? На рассматриваемое тело действует

36

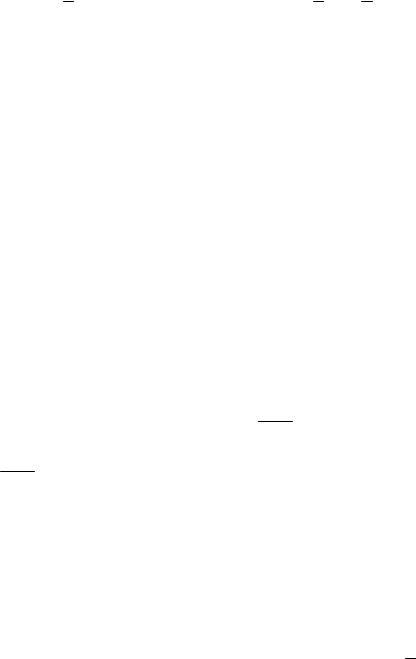
сила тяжести G , две силы реакций опор – N1 и N2 и две силы тре-

ния: Fтр1 = fN1 и Fтр2 = fN2 (мы предполагаем, что коэффициенты трения о вертикальную и горизонтальную опору равны между со- бой). Составим три уравнения равновесия, причем уравнение момен-

тов составляется относительно точки А

ìïN1 - Fтр2 = 0 íFтр1 - G + N2 = 0

ïîN2 2Lsin a - Fтр2 2Lcosa - GLsin a = 0.

Из первого уравнения получаем, что N1 = fN2; с учетом этого из

второго следует, что f2N2 – G +N2 = 0, откуда получаем, что

N2 = G/(1 + f2).

Подставляя это значение в уравнение моментов и разделив его на Lsinα, получаем следующее соотношение:

2G/(1+f2) – 2fG/(1+f2)ctgα - G = 0,

которое после сокращение на G и несложных преобразований приводит нас к формуле: tgα = 12f-f 2 . Таким образом, если

α ≤ arctg12f-f 2 , то независимо от веса тела оно будет находиться в

равновесии.

Перейдем теперь к вопросу о трении качения. Отметим, что сам термин трение качения неверен, так как при качении тела по некото-

рой поверхности не происходит скольжения одной поверхности по другой и степень обработки этих поверхностей значения не имеет. Поэтому сопротивление при качении тел вызывается несколько дру- гими механизмами.

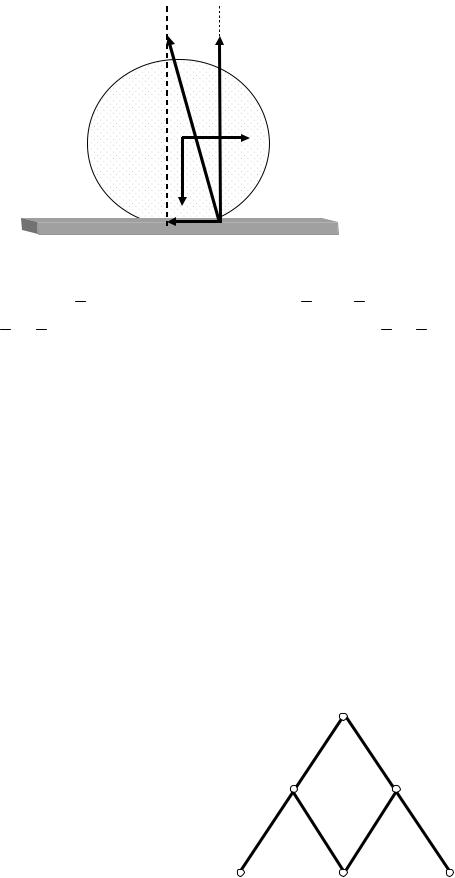
При качении тела радиуса R под действием силы F непременно происходит деформация как самого тела, так и той поверхности, по которой происходит качение. В связи с этим катящееся тело весом Р во время движения как бы накатывается на некоторый порог, в связи с

чем нормальная реакция несколько смещена от середины площадки соприкосновения с поверхностью в сторону качения. Кроме того, эта

нормальная реакция направлена под некоторым углом к вертикали

(рис.3.19).

37

μ

N N1

P F

N2

Рис. 3.19

Раскладывая силу N на две составляющие N1 и N2 получаем, что пара сил ( N2 , F) приводит тело в движение, а пара ( N1 , P) вы-

зывает сопротивление качению, поэтому при качении возникает не сила трения, а момент сопротивления.

Рассмотрим, при каких условиях тело будет двигаться равно- мерно, то есть находиться в равновесии. Запишем три уравнения рав- новесия:

F − N2 = 0, N1 − P = 0, N1μ − N2R = 0.

Последнее из равенств представляет собой уравнение моментов относительно центра тела; μ - коэффициент трения качения, имеющий размерность длины. Из этих уравнений следует, что:

Pμ − FR = 0.

38

честве шарниров, называемых узлами.

Найдем соотношение между количеством стержней n и узлов s в простейших фермах (рис.3.20). Основой построения простейшей фермы является треугольник АВС, то есть трем шарнирам соответст- вуют три стержня. Для присоединения каждого следующего шарнира потребуются два стержня. Таким образом,

n = 3 + 2( s – 3 ) = 2s – 3.

Основной нашей задачей будет определение внутренних сил,

возникающих в стержнях фермы под действием активных внешних нагрузок и реакций опор. При этом мы будем предполагать отсутст- вие трения в шарнирах, абсолютную твердость стержней, а также факт приложения внешних сил только в узлах фермы.

При этих предположениях стержни будут или растянуты, или сжаты.

Конечно, три введенных предположения не соответствуют точно действительности — их можно рассматривать как средство получения первого приближения к величине истинных внутренних усилий, воз- никающих в стержнях фермы под действием внешних сил. В реаль- ных фермах стержни соединены между собой не шарнирно, а посред- ством сварки или заклепок. Поэтому в стержнях фермы возникает, кроме растяжения или сжатия, изгиб. Однако согласно исследованиям академика Е. О. Патона напряжения от изгиба невелики, ими можно пренебречь.

Второе предположение является обычным для статики абсолютно твердого тела. Практическое значение погрешностей, связанных со вторым предположением, также невелико.

Третье предположение не приводит к значительным ошибкам при определении внутренних сил в стержнях фермы, если отношения длин стержней к пролету фермы малы.

Во всяком случае, приближенное решение задачи о распределе- нии внутренних сил в стержнях фермы, найденное на основании трех приведенных выше предположений, в большинстве случаев может

найти практическое применение при технических расчетах элементов фермы на прочность.

Покажем теперь, что задача определения внутренних сил в стержнях простейших ферм статически определенна. Действительно, пусть количество узлов в ферме равно s. Для каждого узла можем со- ставить два аналитических условия равновесия каждого узла как точ- ки, находящейся под действием системы сходящихся сил на плоско-

39

сти. Всех уравнений равновесия мы получим 2s. Эти уравнения будут одновременно включать три уравнения равновесия фермы в целом.

Следовательно, из 2s уравнений мы должны найти 2s-3 внутрен- них сил в стержнях фермы и три реакции опор фермы — всего 2n не- известных, то есть столько же, сколько и стержней в ферме. Эта зада- ча статически определенна.

Задачу определения внутренних сил в стержнях ферм можно ре- шать двумя способами: графическим и аналитическим.

Мы приведем далее примеры аналитических способов определе- ния внутренних сил в стержнях ферм. Условимся внутренние силы, возникающие в стержнях ферм, называть усилиями. Простейший

способ определения усилий в стержнях ферм основывается на методе вырезания узлов. Прежде чем определять усилия в стержнях фермы, надо сначала найти все внешние реакции, хотя формально условия

равновесия узлов фермы содержат в себе условия равновесия фермы в целом, а следовательно, позволяют найти и внешние реакции. Все же предварительное определение реакций позволяет существенно упро- стить решение задачи.

Определение усилий в стержнях фермы производится по сле- дующему алгоритму:

1.Составляются три уравнения равновесия для определения ре- акций опор.

2.Вырежем узел, в котором сходятся не более двух неизвестных усилий.

3.Направим векторы сил, соответствующие усилиям в стержнях, в направлении от узла.

4.Для каждого узла составим два уравнения равновесия для схо- дящейся системы сил.

Если внутренние усилия положительны, то стержень растянут,

если отрицательные – то сжат.

Рассмотрим пример расчета усилий в стержнях про- стейшей фермы (рис.3.21). На рисунке изображена ферма, состоящая из 9 стержней и 6 узлов (9 = 2·6 – 3), причем AC=AD=BD=a. На ферму действуют две силы: F1=40 н, F2=20 н. Обозначим через XA, YA,YB реакции шарниров в точках А и

В. Тогда уравнения равновесия примут вид:

XA − F2cos45o = 0 ; −F2sin450 − F1 + YA + YB = 0;

40