
Учебное пособие ТеорМех
.pdf
1. Если ωпер = 0 , т.е. в случае поступательного переносного
движения.
2. Если vотн = 0 , т.е. в случае относительного покоя точки.
3. Если sin α = 0, т.е. когда относительная скорость точки па- раллельна оси вращения.
Направлен вектор акор , так же как и вектор ω × vотн , т.е. пер- пендикулярно плоскости, проходящей через векторы vотн и ω , в ту
сторону, откуда кратчайшее совмещение этих векторов видно проис- ходящим против хода часовой стрелки.
Для определения направления кориолисова ускорения удобно пользоваться правилом Жуковского: чтобы найти направление кориолисова ускорения, следует спроектировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90о в сторону переносного вращения.
Рассмотрим пример: |
|
|
|
|
Дано: R = 25 см, |
O2 |
|
|
|
ϕпер = 4t − 0,2 t2рад , |
|
|
|
|
|
D |
|
О |
|
OM = π t2 см t1 = 5 c. |
|
|
||
|
|
|
||
4 |
|
|
|
|
Найти в заданный момент вре- |
|
R |
М |
|
мени абсолютную скорость и абсо- |
|
|
|
|
лютное ускорение точки М. Показать |
|
|
|
|
на чертеже положение точки в мо- |
|
|
|
|
мент времени t1 , а также найденные |
|
|
|
|
векторы скорости и ускорения. |
|
|
|
|
Решение. Абсолютное движение |
А |
|
|
|
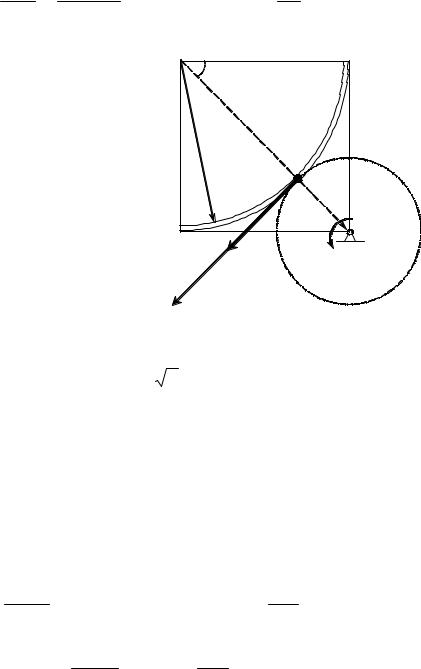
точки М относительно неподвижной |
Рис. 8.6 |
ϕпер |
О1 |
|
плоскости, в которой вращается рам- |
|
|
|
|
ка D, является сложным и состоит из двух движений: относитель- ного по рамке и переносного вместе с рамкой.
Для определения относительного движения мысленно остановим рамку (исключим переносное движение), тогда точка движется по дуге окружности OM, т.е. эта дуга траектория относительного движения точки М. Относительное движение точки задано естест- венным способом. Найдем положение точки М на относительной траектории:
101

sотн = OM(t = 5) = π4 × 52 = 254× π (см).
Угол, на который повернулась точка М за 5с вокруг центра О2
ÐOO2M = |
sотн (5сек) |
= |
25π 4 |
= |
π (рад), |
|
R |
25 |
|||||
|
|
|
4 |
т.е. точка в рассматриваемый момент времени находится на бис- сектрисе ÐOO2M в положении М1.
Относительная скорость точки М
vотн = |
dsотн |
|
d t |
||
|
В заданный момент времени
|
π |
|
|
π |
|
æ |
см ö |
|
= |
4 |
× 2t |
= |
2 |
× t |
ç |
|
÷. |
|
||||||||
|
|
|
|
è |
c ø |
|||
|
π |
æ |
см ö |
|
vотн (5) = |
2 |
× 5 = 2,5π = 7,85 ç |
|
÷, |
|
||||
|
è |
c ø |
||
причем вектор vотн направлен по касательной к траектории относительного движения, т.е. перпендикулярно O2M вправо
( vотн > 0 ) (рис.8.6).
Относительное ускорение точки М
aотн = aотнτ + aотнn .
Касательное относительное ускорение
τ |
dvотн |
æ π |
ö/ |
|
π |
æ |
см ö |
||
aотн = |
|
= ç |
|
× t÷ |
= |
|
= 1,57 ç |
|
÷ |
d t |
2 |
2 |
|
||||||
|
è |
ø |
|
è c2 |
ø |
||||
и aотнτ направлено так же, как и относительная скорость (рис.8.7). Так как касательное относительное ускорение не зависит от времени и vотн > 0 и aотнτ > 0, то относительное движение точки
равноускоренное.
Нормальное относительное ускорение
|
aотнn = |
vотн2 |
, |
|
ρ |
||
|
|
|
|
|
где ρ = R – радиус кривизны относительной траектории точки |
||
(в |
случае прямолинейного относительного движения ρ = ∞ и |
||
aотнn |
= 0). |
|
|
102
|
|
aотнn |
= |
|
v2 |
|
|
(2,5 π)2 |
|
= 0,25π2 |
|
æ см ö |
|||||||||
|
|
|
отн = |
|
25 |
|
= 2,46 ç |
÷, |
|||||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
è c2 |
ø |
||
и aотнn направлено к центру кривизны |
O2 |
|
π |
|
|
||||||||||||||||
относительной траектории от М к |
|
|
О |
||||||||||||||||||
|
4 |
|
|||||||||||||||||||
О2 (рис.8.7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
переносного |
|
|
|
|
|
|
||||||||
Для |
определения |
|
|
R |
|
|
|||||||||||||||
движения точки М мысленно остано- |
|
|
|
|
|||||||||||||||||
вим в рассматриваемый момент вре- |
|
|
|
D |
М1 |
|
|||||||||||||||
мени точку на относительной тра- |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||
ектории в положении М1 (исключим |
|
|
|
|
|
|
|||||||||||||||
относительное движение). Тогда, |
|
|
|
|
|
О1 |
|||||||||||||||
вращаясь вместе с телом D, точка |
|
А |
vпер |
ϕпер |
|||||||||||||||||
М1 описывает окружность радиуса |
|
|
|
|
|||||||||||||||||
М1О1 с центром в точке О1. Эта ок- |
|
|
|
vотн |
|
|
|||||||||||||||
ружность является переносной тра- |
|
|
|
|
Рис. 8.7 |
||||||||||||||||
екторией точки в момент времени t1 = 5 c. Найдем радиус этой ок- |
|||||||||||||||||||||
ружности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1O1 = O1O2 - O2M1 = R |
2 - R = R × 0,41см . |
||||||||||||||||||
Переносную скорость и переносное ускорение точки найдем как |
|||||||||||||||||||||
скорость и ускорение точки М1, принадлежащей вращающемуся те- |
|||||||||||||||||||||
лу D: |
|
v |
|
|
|
= ω |
|
× M O ; |
|
|
a |
|
|
= aτ |
+ an |
, |
|||||
|
|
пер |
|
пер |
|
|
пер |
||||||||||||||
|
aτ |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
пер |
пер |
|
|||||
где |
= ε |
пер |
× M O , |
|
|
an |
|
= ω2 |
|
× M O . |
|
|
|||||||||
|
пер |
|
|
|
1 |
1 |
|
|
|
пер |
|
пер |
|
1 1 |
|
|
|||||
Найдем угловую скорость и угловое ускорение переносного дви- |
|||||||||||||||||||||
жения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωпер |
|
= |
dϕпер |
|
= 4 - 0,2 × 2t |
= 4 - 0,4 × t |
æ рад |
ö |
|||||||||||
|
|
|
d t |
|
ç |
÷ . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è c |
ø |
||
|
|
|
|
|
|
|
|
εпер |
|
= |
dωпер |
= -0,4 |
æ |
рад ö |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
d t |
ç |
÷. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
c2 ø |
|
|
|
Поскольку ωпер > 0, |
εпер < 0 и |
|
εпер |
не зависит от времени, то |
|||||||||||||||||
переносное вращение равнозамедленное. |
|
|
|
|
|
|
|||||||||||||||
В рассматриваемый момент времени |
|
|
|
|
|||||||||||||||||
vпер (5) = ωпер (5)× M1O1 |
æ |
см ö |
|
= 2× 25×0,41 = 20,5 ç |
|
÷ . |
|
|
|||
|
è |
c ø |
|
Вектор vпер направлен перпендикулярно М1О1 в сторону пере- носного вращения (рис.8.7).
103
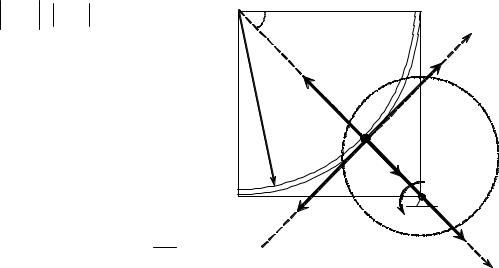
Касательное переносное ускорение |
|
|
|
|
|||
aτ |
= ε |
|
|
|
æ |
см ö |
|
пер |
(5) × M O = 0,4 |
× 25× 0,41 = 4,1 |
ç |
|
÷ . |
||
|
|||||||
пер |
|
1 1 |
|
è c2 ø |
|||
|
|
|
|
|
|||
Вектор aперτ направлен противоположно vпер (рис.8.8).
Нормальное переносное ускорение
an |
= (ω |
|
2 |
× M O = 22 |
æ |
см ö |
пер |
(5)) |
× 25 × 0,41 = 41 ç |
÷. |
|||
пер |
|
|
1 1 |
è c2 ø |
||
|
|
|
|
|
||
Вектор aперn направлен от точки М1 к О1 (рис.8.8).
Для определения абсолютной скорости применим теорему о сложении скоростей в сложном движении
vабс = vотн + vпер .
В данной задаче векторы vотн и vпер направлены в одну сторону вдоль одной прямой (рис. 8.7), следовательно, модуль vабс :
æ |
см ö |
|
vабс = vотн + vпер = 7,85 + 20,5 = 28,35 ç |
|
÷ . |
|
||
è |
c ø |
|
Абсолютное ускорение найдем по теореме Кориолиса
aабс = aотн + aпер + aкор . |
(8.5) |
Ускорение Кориолиса
aкор = 2 ×[ωпер , vотн ].
Определим модуль ускорения Кориолиса
a |
кор |
= 2 ω |
× v |
отн |
× sin (ω |
, v |
|
) |
π |
|
О |
Х |
|
|
пер |
|
|
пер |
|
отн O2 |
|
||||||
|
|
|
. |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переносное |
вращение |
проис- |
|
R |
aотнn |
|
aперτ |
||||||
ходит вокруг оси, перпендикуляр- |
|
|
|
||||||||||
|
|
|
М1 |
|
|||||||||
ной плоскости рамки D, поэтому |
|
D |
|
|
|||||||||
угол |
между переносной |
угловой |
|
|
|
aперn |
|
||||||
скоростью ωпер |
и относительной |
|
|
|
|
О1 |
|||||||
линейной vотн равен 90°, тогда |
|
|
|
А |
|
|
|||||||
|
|
|
aотнτ |
ϕпер |
aкор |
||||||||
|
|
|
|
|
|
æ см ö |
|
|
|
||||
aкор |
|
|
|
|
|
|
|
|
|
Y |
|||
= 2 × 2 × 7,85 ×1 = 31,4 ç |
÷. |
|
|
Рис. 8.8 |
|||||||||
|
|
|
|
|
|
è c2 ø |
|
|
|
|
|||
104

Для определения направления aкор в данной задаче вектор отно-
сительной скорости необходимо повернуть на прямой угол в направ- лении переносного вращения, т.е. вектор aкор направлен от М1 к О1
(рис.8.8).
Абсолютное ускорение найдем методом проекций, для чего ось
Хнаправим по М1О1.
Вразвернутом виде (1) можно записать
aабс |
= aотнτ + aотнn |
+ aперτ + aперn + aкор . |
|
|
|
|
|
|
|
(8.6) |
||||||||
Запишем выражение (8.6) в проекциях на оси М1ХУ |
|
|
|
|
|
|
|
|
||||||||||
aабс X = -aотнn + aперn |
|
|
|
|
|
|
|
|
|
|
|
æ см ö |
||||||
+ aкор |
= -2,46 + 41+ 31,4 = 69,94 ç |
|
|
÷; |
||||||||||||||
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è c |
ø |
|||
aабс Y = -aотнτ |
+ aперτ |
|
|
|
æ см |
ö |
|
|
|
|
|
|||||||
= -1,57 + 4,1 = 2,53 ç |
|
|
÷. |
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
è c |
ø |
|
|
|
|
|
|||
По теореме Пифагора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
см ö |
|
|
|||
aабс = aабс2 |
Х + aабс2 |
|
|
|
69,942 + 2,532 » 70 |
|
|
|||||||||||
Y = |
ç |
|
|
|
÷ . |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
è c2 |
ø |
|
|
||||
Вопросы для самопроверки
1.Какое движение называют переносным (относительным, абсолютным)?
2.Чему равна абсолютная скорость точки в сложном движении?
3.Как направлен вектор переносной скорости точки?
4. Как определить абсолютное ускорение точки в сложном движении?
5.Как найти направление вектора абсолютного ускорения точки в сложном движении?
6.В каких случаях модуль ускорения Кориолиса равен нулю?
105

РАЗДЕЛ ТРЕТИЙ
ДИНАМИКА ТОЧКИ И СИСТЕМЫ
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил. В этом разделе, в от- личие от кинематики, при изучении движения тел принимают во вни- мание как действующие на них силы, так и инертность самих матери- альных тел. Инертность тела проявляется в том, что оно сохраняет свое движение при отсутствии действующих сил, а когда силы начи- нают на него действовать, то скорости точек тела изменяются не мгновенно, а постепенно и тем медленнее, чем больше инертность этого тела. Количественной мерой инертности материального тела является физическая величина, называемая массой тела. Одной из
важнейших характеристик движения материальной точки является ее
количество движения. Это векторная величина mv , равная произведению массы точки на ее скорость. Направлен вектор mv так же, как и вектор скорости точки, т.е. по касательной к траектории.
Единицей измерении количества движения в системе СИ является [Н·с].
ГЛАВА IХ ДИНАМИКА ТОЧКИ
§ 1. Законы динамики. Задачи динамики.
В основе динамики лежат законы, сформулированные Ньютоном:
1.Закон инерции. Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние.
2.Закон равенства действия и противодействия. Две матери-
альные точки действуют друг на друга с силами, равными по модулю и направленными вдоль одной прямой, соединяющей эти точки, в противоположные стороны.
Последний закон нам уже встречался в первой главе.
Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу; 2) зная действующие на точку силы, определить закон движения точки (основная задача динамики).
106

§2. Теорема об изменении количества движения точки. Импульс силы.
Одним из важнейших базовых постулатов динамики является положение о том, что фактором, влияющим на изменение количества движения точки, являются силы, действующие на эту точку. Этот по-
стулат носит название теоремы об изменении количества движения точки в дифференциальной форме:
|
d(mv) |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
= å |
|
|
|
|
|
|
|
|
|
|
(9.1) |
|||||
|
Fi . |
||||||||||||||||
|
|
dt |
|||||||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|||||
Так как силы, действующие на точку, являются сходящейся |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
системой сил, то они имеют равнодействующую |
|
= å |
|
|
и формула |
||||||||||||
R |
Fi |
||||||||||||||||
(9.1) примет вид: |
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
d(mv) |
= |
|
. |
|
|
|
|
|
|
|
|
|
(9.2) |
||
|
|
R |
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Умножив формулу (9.2) на dt и проинтегрировав на промежутке |
|||||||||||||||||
|
|
t 2 |
|
|
|
|
t 2 |
|
|||||||||
времени от t1 до t2, получим: òd(mv) = |
|
ò |
|
|
|
|
|||||||||||
|
Rdt , или |
|
|||||||||||||||
|
|
t1 |
|
|
|
|
|
t1 |
|
||||||||
|
|
|
|
|
|
t 2 |
|
||||||||||
mv2 - mv1 = ò |
|
|
(9.3) |
||||||||||||||
Rdt . |
|||||||||||||||||
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
Для характеристики действия, оказываемого на тело некоторой силой за некоторый промежуток времени, используются понятие импульса силы. Введем понятие элементарного импульса силы, т.е. импульса за элементарный промежуток времени dt. Элементарным импульсом силы называется векторная величина dS , равная произве- дению силы F на элементарный промежуток времени dt
dS = F × dt .
Направлен элементарный импульс вдоль линии действия силы. Импульс S любой силы F за время t2-t1 вычисляется как предел
интегральной суммы соответствующих элементарных импульсов, т.е.
t 2
S = ò F × dt .
t1
Импульс силы за некоторый промежуток времени равен опреде- ленному интегралу от элементарного импульса, взятому в пределах от
107
t1 до t2. Если сила F постоянна по модулю и направлению, то |
S = F × t |
||||||
и модуль S = F× t . Единицей измерения импульса силы в системе СИ |
|||||||
является [Н·с]. |
|
|
|
|
|
|
|
|
Таким образом, формула (9.3) выражает теорему об изменении |
||||||
количества движения точки в интегральной форме: изменение ко- |
|||||||
личества движения точки за некоторый промежуток времени |
|||||||
равно сумме импульсов всех действующих на точку сил за тот же |
|||||||
промежуток времени. |
|
|
|
|
|
||
|
Учитывая, что a = dv |
, в случае постоянной массы точки |
урав- |
||||
|
|
dt |
n |
|
|
|
|
|
|
|
|
|
|
|
|
нение (9.1) примет вид: ma = åFi , которое обычно называют вторым |
|||||||
законом Ньютона. |
i=1 |
|
|
|
|
||
|
|
|
|
|
|||
|
§ 3. Дифференциальные уравнения движения точки. |
|
|||||
|
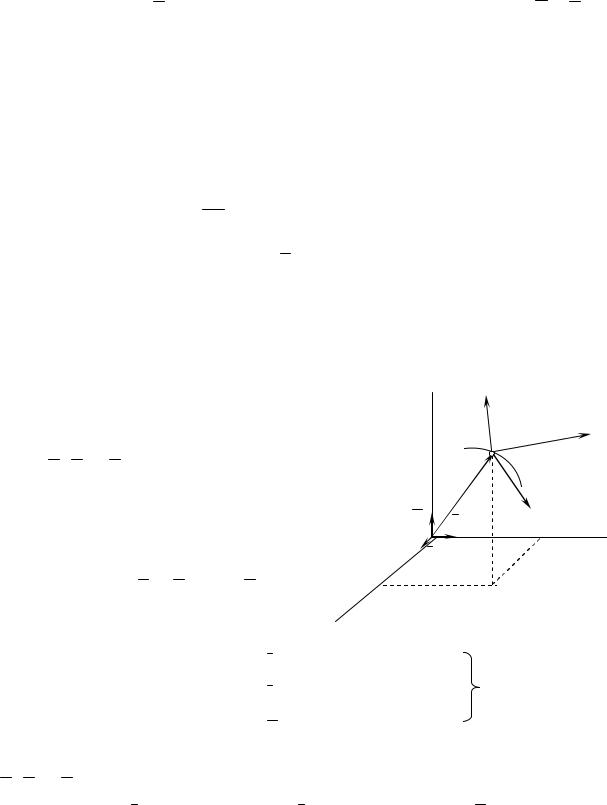
Рассмотрим |
движение матери- |
|
z |
Fn |
|
|
альной точки М постоянной массой |
|
|
|
F1 |
|||
m под действием приложенных к ней |
|
|
М |
|
|||
сил |
F1, F2 ,...Fn |
(рис.9.1). |
Выберем |
|
|
r |
|
прямоугольную |
систему |
координат |
|
|
F2 |
||
|
|
z |
|||||
х,у,z. |
|
|
|
k |
|
||
|
|
|
j |
y |
|||
|
В этом случае основное уравне- |
|
i |
|
|
||
ние динамики имеет вид: |
|
|
y |
|
|||
|
ma = F1 + F2 + ... + Fn . |
x |
x |
|
|
||
|
Спроектируем это векторное ра- |
|
Рис. 9.1 |
|
|||
венство на координатные оси: |
|
|
|
|
|||
|
|
ma(cos a, i) = Fx1 + Fx2 + ... + Fxn |
|
|
|||
|
|
ma(cos a, j) = Fy1 + Fy2 + ... + Fyn |
|
|
|||
|
|
ma(cos a, k) = Fz1 + Fz2 + ... + Fzn |
|
|
|||
|
Где Fх1,Fy1, Fz1, Fх2 , Fy2 , Fz2 ,..., Fхn , Fyn , Fzn |
– проекции сил |
|
||||
F1, F2 ,...Fn на оси х,у,z. Так как |
|
|
|
|
|||
|
a(cos a, i) = ax = &x& ; a(cos a, j) == a y = &y&; a(cos a, k) = az |
= &z&, |
|||||
|
то |
|
|
|
|
|
|
|
|
|
108 |
|
|
|
|

mx = Fx1 + Fx2 + ... + Fxn |
= åFkx |
|
&& |
= åFky |
|
my = Fy1 + Fy2 + ... + Fyn |
(9.4) |
|
&& |
= åFkz |
|
mz = Fz1 + Fz2 + ... + Fzn |
|
|
&& |
|
|
Уравнения (9.4) называются дифференциальными уравнения-
ми движения точки.
Отметим, что основное уравнение движения может быть записа- но в несколько другой форме, схожей с формой записи уравнения равновесия. Обозначим в записи второго закона Ньютона Ф = −ma и перенесем все слагаемые в левую часть. Получим:
F1 + F2 + ... + F + Ф = 0.
Сила Ф , равная произведению массы точки на ее ускорение и направленная противоположно ускорению, называется силой инер- ции.
Последнему равенству можно дать такую трактовку: если в каж-
дый момент времени к фактически действующим на точку силам прибавить силу инерции, то полученная система сил бу-
дет уравновешенной. Это положение, эквивалентное второму за- кону Ньютона, выражает принцип Даламбера.
§ 4. Решение основной задачи динамики.
Движение материальной точки будет прямолинейным, когда рав- нодействующая всех приложенных сил имеет постоянное направле- ние, а скорость в начальный момент времени равна нулю или направ- лена вдоль силы.
Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений (9.4)
mx = åFkx . |
(9.5) |
&& |
|
Это уравнение называют дифференциальным уравнением прямолинейного движения точки. Для решения основной задачи динамики его надо проинтегрировать. В полученное решение войдут две постоянные интегрирования С1 и С2 и общее решение такого уравнения будет иметь вид: x = f (t,С1,С2 ) . При определений С1 и С2
понадобятся начальные условия.
Изучение всякого движения начинают с некоторого определен- ного момента времени, называемого начальным моментом. От этого
109

момента отсчитывают время движения, считая, что в начальный мо- мент времени t=0. Обычно, за начальный принимают момент начала движения под действием заданных сил. При этом положение точки называют начальным положением, а ее скорость – начальной ско-
ростью. В случае прямолинейного движения начальные условия за-
дают в виде: при t = 0 x = xo |
x = vo . По начальным условиям оп- |
|
& |
ределяются С1 и С2 и находится частное решение уравнения (9.5) в
виде x = f (t, хо , vо ).
В случае криволинейного движения точки на плоскости основная задача динамики решается с помощью двух уравнений системы (9.4). Проинтегрировав эти уравнения, находят координаты х, у движущей- ся точки как функции от времени t, т.е. определяют закон движения движущейся точки. Решение будет содержать четыре постоянных интегрирования С1, С2, С3 и С4. Начальные условия, необходимые для
их |
определения |
задаются |
|
|
в |
|
виде: |
||
t = 0 x = xo x& = vxo y = yo y& = vyo . |
|
|
|
|
|
||||
|
Рассмотрим пример плоского движения точки М с на- |
||||||||
|
чальной скоростью v0 под действием силы тяжести без со- |
||||||||
|
противления воздуха. В этом случае нам необходимы два |
||||||||
|
уравнения движения из системы (9.4). Так как на точку дей- |
||||||||
|
|
|
ствует только сила тяжести, они при- |
||||||
y |
|
|
мут вид: mx = 0, my = −mg, где g – ус- |
||||||
M |
|
|
&& |
&& |
|
|
|
|
|
|
|
корение силы тяжести (рис.9.2). Интег- |
|||||||
vo |
mg |
|
рируя два раза последние уравнения, по- |
||||||
α |
|
лучаем: |
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
h |
|
|
x = C1 |
, y = −gt + C2 |
|
|
|
(9.6) |
|
|
|
x = C t + C |
, y = − gt |
2 |
+ C |
t + C |
|||
|
|
|
|
4 |
|||||
|
|
x |
1 |
3 |
2 |
2 |
|
||
|
Рис. 9.2 |
|
|
|
|
|
|||
|
Отметим, что пока положение на- |
||||||||
|
|
||||||||
чала координат нам не понадобилось. Как видно из уравнений (9.6), для получения решения нам необходимо определить четыре постоян- ные: С1, С2, С3, С4. Это делается с помощью начальных условий: на- чального положения точки и начальной ее скорости. Здесь необходим выбор начала координат. Выбрав его, как показано на рис.9.2, мы по- лучаем, что при t=0 x = 0, x& = v0 cos α, y = h, y& = v0 sin α . Подставляя
эти условия в систему (9.6), получаем: С1=v0cosα, С3=0, С2=v0sinα, С4=h. Тогда уравнения движения точки примут вид:
110
