
Учебное пособие ТеорМех
.pdf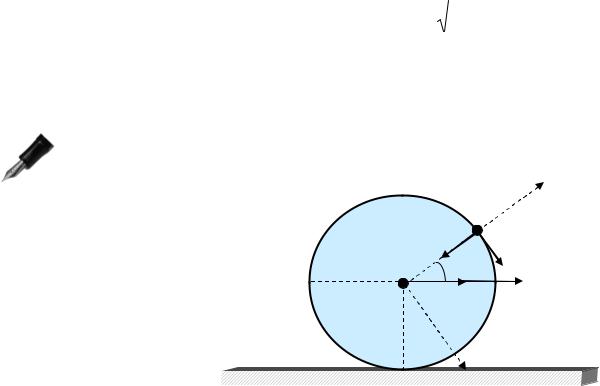
aB = |
ε × OA cosβ + ω2 |
× OA sin β + ωBA2 |
× BA |
. |
|
cos α |
|
||
|
|
|
|
Подставив найденное значение ускорения точки В во второе уравнение системы (7.8), можно определить угловое ускорение εВА, которое нам понадобится для определения ускорения точки С.
Ускорение точки С также определяется по формуле (7.6):
аC = аB + аτCB + аnCB . |
(7.9) |
Отметим, что в качестве полюса можно было бы выбрать точку А. Проектируя равенство (7.9) на оси x и y, получим
ì |
|
|
|
n |
|
ïaCx |
= aB cos α - aCB |
. |
|||
í |
|
= -a |
|
sin α + aτ |
|
ïa |
Cy |
B |
|
||
î |
|
CB |
|
||
Отметим, что в случае нахождения ускорения точки В нам не было известно угловое ускорение АВ, но было известно направление ускорения точки В. Направление ускорения точки С нам сейчас неиз- вестно, поэтому мы и определяем сначала его проекции на оси коор- динат aCx и aCy . Зато мы знаем εВА, что поможет нам определить
ускорение точки С по формулам:
ì |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||
ïaCx |
= aB cos α - ωAB × BC |
, |
aC = |
|
|||||||
í |
|
= -a |
|
sin α + ε |
|
× BC |
aCx + aCy . |
||||
ïa |
Cy |
B |
AB |
|
|
|
|
|
|||
î |
|
|
|
|
|
|
|
|
|||
Одним из часто встречаемых видов движения является качение однородного диска (цилиндра) по горизонтальной плоскости.
|
|
Рассмотрим следующий пример . Пусть центр диска A |
|||||
|
радиуса |
R, |
ка- |
|
|
x |
|
|
тящегося |
по |
|
|
|||
|
горизонтальной |
|
|
B |
|||
плоскости, имеет в дан- |
|
|
|||||
|
aBAn |
aBAτ |
|||||
ный момент |
времени |
|
|||||
скорость v и ускорение а |
|
α |
|
||||
(рис.7.18). |
Требуется |
A |
aA |
vA |
|||
определить |
ускорение |
R |
|
|
|||
точки |
В, |
расположен- |
|
y |
|||
ной как |
показано на ри- |
|
|
||||
сунке. По формуле (7.6) |
Рис. 7.18 |
|
|||||
аB = аА + аτBA + аn BА . |
|
||||||
Проектируя это равенство на оси x и y, получим
91

|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
× AB |
|
|||
|
|
|
ïaBx = aA cos α - ω |
|
|
|
. |
|||||||||||||
|
|
í |
|
|
|
= a |
|
sin α + ε × AB |
||||||||||||
|
|
|
ïa |
By |
A |
|
||||||||||||||
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Учитывая, что ω = |
vA |
= |
|
v |
|
и ε = |
aA |
= |
|
|
a |
, получаем |
||||||||
|
|
R |
|
|
|
|
||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
R |
|
R |
|
||||||
|
|
|
|
ì |
|
|
|
= a cos α - v |
2 |
|
|
|||||||||
|
|
|
|
|
ïa |
Bx |
|
|
|
|||||||||||
|
|
|
|
í |
|
|
|
|
|
|
R . |
|
||||||||
|
|
|
|
ï |
|
|
|
= a sin α + a |
|
|
|
|
||||||||
|
|
|
|
|
îaBy |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ì |
|
= - v |
2 |
|
|
||||
В частности, если а=0, то |
ïa |
Bx |
|
|
|
|
||||||||||||||
í |
|
R , то есть ускорение на- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ï |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îaBy |
|
|
|
|
|
|
|||
правлено к центру диска и имеет величину v2 /R. |
|
|||||||||||||||||||
Если же α = - |
π , то есть точка В – точка касания с плоско- |
|||||||||||||||||||
ì |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= - v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ïa |
Bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
стью, то также í |
|
|
|
R , то есть ускорение направлено к цен- |
||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îaBy = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тру диска и имеет величину v2 /R.
§10. Мгновенный центр ускорений
При непоступательном движении плоской фигуры у нее в каж- дый момент времени имеется точка Q, ускорение которой равно ну- лю. Эта точка называется мгновенным центром ускорений. Опреде- ляется положение центра Q, если известны ускорение aA какой-
нибудь точки А фигуры и величины ω и ε, следующим путем:
1)находим значение угла μ из формулы tgμ = ωε2 ;
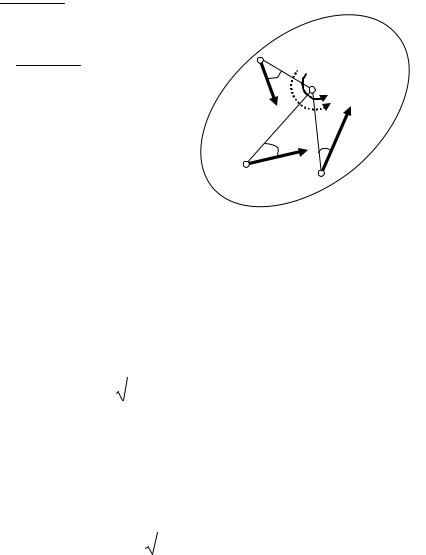
2)от точки А под углом μ к вектору aA проводим прямую АЕ (рис.7.19); при этом прямая АЕ должна быть отклонена от aA в сто-
рону вращения фигуры, если вращение является ускоренным, и про- тив вращения, если оно является замедленным, т. е. в сторону направ- ления углового ускорения ε;
3) откладываем вдоль линии АЕ отрезок AQ, равный
AQ = |
aA |
(7.10) |
ε2 + ω4 |
92
Построенная таким путем точка Q и будет мгновенным центром ускорений. В самом деле, по известным формулам aM = aA + aMA и
аМА = МА
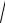 ε2 + ω4 :
ε2 + ω4 :
aQ = aA + aQA ,
где численно аQА = QА
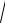 ε2 + ω4 . Подстав-
ε2 + ω4 . Подстав-
ляя сюда значение AQ из равенства (7.10), находим, что aA = aQA . Кроме того, вектор
М |
ω |
μ |
Q |
aM |
ε |
aB |
|
μ |
μ |
aQA должен образовывать с линией AQ |
А |
a |
A |
В |
||
угол μ, следовательно, вектор aQA паралле- |
|
|||||
|
|
|
|
|||
лен aA , но направлен в противоположную |
Рис. 7.19 |
|
||||
сторону. Поэтому aQA = −aA и aQ = 0. |
|
|
|
|
||
Если точку Q выбрать за полюс, то так как aQ = 0, ускорение лю- |
||||||
бой точки М тела согласно формуле aM = aA + aMA будет |
|
|
||||
aM = aQ + aMQ = aMQ . |
|
|
|
|
||
При этом из равенств (7.10) следует, что численно |
|
|
|
|||
|
|
|
|
|
||
аM = QM |
ε2 + ω4 |
. |
|
|
|
(7.11) |
Следовательно, ускорения точек плоской фигуры определяют-
ся в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра ускорений Q. При этом, как следует из (7.11),
аM |
|
аA |
|
|
||
= |
= ... = |
ε2 + ω4 |
(7.12) |
|||
QM |
QA |
|||||
|
|
|
|
|||
т. е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгновенного центра ускорений. Картина распределе-
ния ускорений (т. е. поле ускорений точек плоской фигуры в данный момент времени) показана на рис.7.19.
Следует иметь в виду, что положения мгновенного центра скоро- стей Р и мгновенного центра ускорений Q в данный момент времени не зависят друг от друга.
Например, если колесо катится по прямолинейному рельсу, при- чем скорость его центра С постоянна, то мгновенный центр скоростей находится в нижней точке Р, следовательно, точка Р не является од- новременно мгновенным центром ускорений. Мгновенный центр ус- корений в этом случае находится, очевидно, в центре колеса, так как он движется равномерно и прямолинейно. Центры скоростей и уско-
93
рений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.
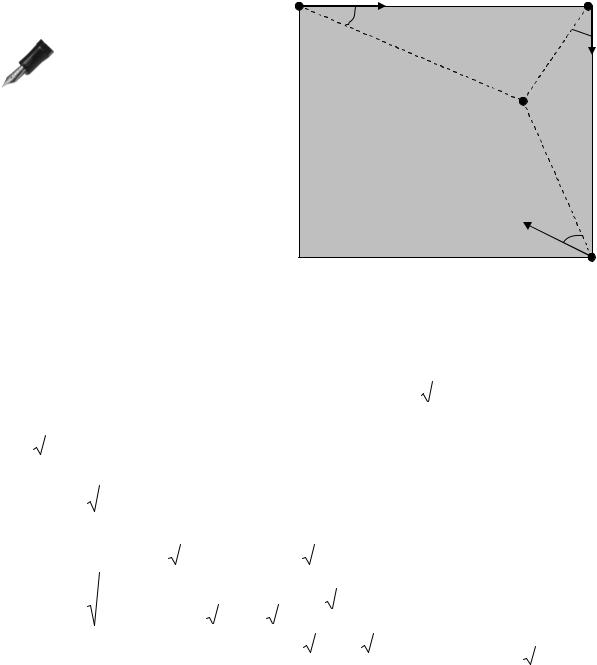
Рассмотрим следующий пример. Дан квадрат со стороной b. Ускоре-
ние точки А равно 2a,ускорение точки В равно а. Найти ускорение точки D (рис.7.20). По условию мгновен-
ный центр ускорений должен находиться в два раза дальше от точки А, чем от точки В, то есть AQ=2BQ. Как видно из рисунка, треугольник ABQ – прямоугольный и tgα = 0,5. От-
A |
aA |
B |
|
|
α |
|
aB |
|
|
α |
|
|
|
Q |
|
aD α
D
Рис. 7.20
резок BQ равен bsinα. Так как |
|
sin2 α + cos2 α = 1, |
то, разделив на |
|||||||||||||||||||||||||||||||||||||||||||
sin2 α , получим 1+ ctg2α = |
1 |
|
|
. Тогда sin α = |
1 |
|
|
, то есть BQ ра- |
||||||||||||||||||||||||||||||||||||||
sin2 |
α |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
5 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
вен |
|
. По теореме косинусов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
DQ = |
BQ2 + BD2 - 2 × BQ × BD × cos α |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Так как sin α = |
1 |
|
|
, то cos α = |
|
2 |
|
. Тогда |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
5 |
5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
DQ = |
b2 + b2 |
- 2 × |
b |
|
|
× b × |
|
2 |
|
|
|
|
= b |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 / 5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
5 |
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
aD |
|
|
DQ |
= |
b |
|
|
× |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
И окончательно, |
= |
|
2 / 5 |
5 |
, откуда aD = a |
|
. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
BQ |
|
|
|
|
|
b |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
aB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
94
Вопросы для самопроверки
1.Какое движение твердого тела называют поступательным?
2.Как определить угловую скорость вращательного движения твердого тела?
3.Куда направлен вектор углового ускорения?
4.Что называют осью вращения?
5.Какое движение твердого тела называют плоским?
6.Что такое мгновенный центр скоростей?
7.В чем заключается теорема о проекциях скоростей двух точек тела?
8.Как найти мгновенный центр скоростей?
9.Что необходимо знать для определения скорости точки в плоском движении?
10.Что такое мгновенный центр ускорений?
11.Как найти мгновенный центр ускорений?
12.Как определить линейную скорость точки на вращающемся теле?
13.Что необходимо знать для определения ускорения точки
в плоском движении?
95

ГЛАВА VIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§1. Относительное, переносное и абсолютное движения
Сложное движение точки – это такое движение, при котором точка одновременно участвует в двух или нескольких движениях. На- пример, сложное движение совершает пассажир, перемещающийся по вагону движущегося поезда; сложное движение также совершает лод- ка, переплывающая реку.
В этом случае движение точки рассматривают по отношению к двум системам отсчета, одна из которых считается основной или ус- ловно неподвижной, а другая определенным образом движется по от- ношению к первой. В приведенных примерах к неподвижным систе- мам отсчета относят системы, связанные с железнодорожными рель- сами или с берегом реки, а подвижными будут системы, связанные с поездом или с течением реки.
Таким образом, сложное движение разлагается на два более про-
стых. Рассмотрим точку М, кото- |
|
|
|
|
|
рая движется по отношению к |
z1 |
v |
отн |
B |
vабс |
подвижной системе отсчета Охуz, |
|
|
|
D vпер |
|
которая в свою очередь движется |
|
z |
|
|
|
относительно неподвижной сис- |
|
|
М |
|
m |
темы отсчета О1х1у1z1 (рис.8.1). |
|
|
C A |
y |
|
Движение, совершаемое точ- |
|
|
|||
кой М по отношению к подвиж- |
|
O |
|
|
|
ной системе отсчета Охуz, назы- |
|
|
|
|
|
вается относительным движени- |
|
x |
|
|
|
ем. В этом случае траекторию АВ, |
O1 |
|
|
|
y1 |
по которой движется точка отно- |
|
|
|
|
|
сительно подвижных осей, назы- |
|
|
|
|
|
вают траекторией относительно- |
x1 |
|
|
|
|
го движения. Скорость точки по |
|
Рис. 8.1 |
|
|
|
отношению к осям Охуz называ- |
|
|
|
|
|
ют относительной скоростью ( vотн ),
ускорением (аотн ). Из определения следует, что при вычислении vотн и аотн движение системы координат Охуz можно не учитывать.
Движение, совершаемое подвижной системой отсчета Охуz по отношению к неподвижной системе О1х1у1z1, является для точки М переносным движением. Скорость точки m, связанной с подвижны- ми осями, с которой в данный момент совпадает положение движу- щейся точки М, называют переносной скоростью точки М в этот
96
момент времени ( vпер ), а ускорение точки m – переносным ускорени-
ем точки М (апер ).
Движение, совершаемое точкой М по отношению к неподвижной системе О1х1у1z1, называется абсолютным движением точки. Тра-
ектория CD этого движения называется абсолютной траекторией,
скорость – абсолютной скоростью ( vабн ), а ускорение – абсолютным ускорением (аабс ).
§2. Теорема о сложении скоростей
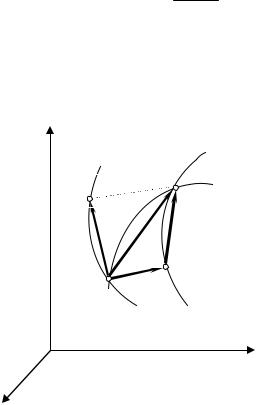
Рассмотрим сложное движение точки М (рис.8.2). Пусть эта точ- ка совершает за промежуток времени t = t1 − t вдоль траектории АВ
относительное перемещение, определяемое вектором MM2 . Сама
кривая АВ, двигаясь вместе с подвижными координатными осями Охуz, перейдет за тот же промежуток времени в какое-то новое поло- жение А1В1. Одновременно та точка m кривой АВ, с которой в мо-
мент времени t совпадает точка |
М, |
|
|
|
|
||||||||||||||||||||||
совершит переносное перемещение |
|
z1 |
|
В1 |
|||||||||||||||||||||||
|
mm1 |
= |
Mm1 |
. В результате точка М |
|
|
B |
М1 |
|||||||||||||||||||
придет в положение М1 и совершит |
|
|
М2 |
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
за время |
|
t абсолютное перемеще- |
|
|
|
|
|||||||||||||||||||||
ние |
MM1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Из векторного |
|
треугольника |
|
|
|
m1 |
||||||||||||||||||
Мm1М1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
М m |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
+ |
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
MM |
Mm |
m M |
1 |
|
|
|
A |
A1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||
на |
|
Деля обе части этого равенства |
O1 |
|
y1 |
||||||||||||||||||||||
|
t и переходя к пределу, полу- |
|
|
|
|
||||||||||||||||||||||
чим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
Рис.8.2 |
|
||||||
|
|
|
|
lim MM1 |
= lim |
Mm1 |
+ lim m1M1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
t→∞ |
|
t |
|
t→∞ |
|
t |
t→∞ |
t |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
Учитывая, что lim |
MM1 |
|
= vабс , |
lim |
Mm1 |
= vпер , а |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t→∞ |
t |
|
|
|
|
t→∞ |
t |
|
|
|||||
|
lim |
m1M1 |
|
= vотн , получаем |
|
|
|
|
|
|
|
|
|||||||||||||||
|
t→∞ |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
vабc = vотн + vпер . |
|
(8.1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
97

Направлены векторы vабс , vотн , vпер по касательным к соответст-
вующим траекториям (рис.8.3).
При сложном движении абсолютная ско- рость точки равна геометрической сумме от- носительной и переносной скоростей. Если угол между векторами vотн и vпер равен α , то
модуль абсолютной скорости можно найти по формуле
B
vотн vабс
М α vпер
|
|
|
|
vабс = v2отн + v2пер + 2vотнvпер cos α . |
A |
||
Рис.8.3
§3. Теорема о сложении ускорений (теорема Кориолиса)
Найдем ускорение точки, совершающей сложное движение как
производную по времени от (8.1) |
|
|
dvпер |
|
|
||||
аабс = |
dv |
абс |
= |
dv |
отн |
+ |
. |
(8.2) |
|
|
|
|
|
dt |
|||||
|
dt |
dt |
|
|
|||||
Производные определяют изменение vотн , |
vпер при абсолютном |
||||||||
движении. Эти изменения складываются из изменений при относи- тельном и при переносном движениях. Введем индексы: 1 – измене- ние скорости при относительном движении, 2 – изменении скорости при переносном движении. В этом случае равенство (8.2) примет вид:
аабс = |
dv |
отн1 |
+ |
dv |
отн2 |
|
+ |
|
|
dvпер1 |
|
+ |
dvпер2 |
. |
(8.3) |
||||||
|
|
dt |
|
|
|
dt |
|
dt |
|||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|||||||||||
Относительное ускорение характеризует изменение относи- |
|||||||||||||||||||||
тельной скорости только при относительном движении |
|
||||||||||||||||||||
|
|
|
|
аотн |
= |
|
dvотн1 |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|||||
Переносное ускорение характеризует изменение переносной |
|||||||||||||||||||||
скорости только при переносном движении |
|
|
|
|
|||||||||||||||||
|
|
|
|
апер |
= |
dvпер2 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|||||
В результате равенство (8.3) принимает вид |
|
|
|||||||||||||||||||
аабс |
= аотн + апер + |
|
dv |
отн2 |
|
+ |
|
dvпер1 |
. |
|
|||||||||||
|
dt |
|
dt |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
98
dvотн2 + dvпер1 . Величина акор , характери- dt dt
зующая изменение относительной скорости точки при переносном движении и переносной скорости при ее относительном движении, называется поворотным, или кориолисовым, ускорением точки. С учетом этого окончательно получаем
аабс = аотн + апер + акор |
(8.4) |
При сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и кориолисова.
Найдем формулу для вычисления кориолисова ускорения. Име-
ем:
акор = dvотн2 + dvпер1 .
dt dt
Сначала определим
dvотн2 . Пусть переносное dt
движение складывается из поступательного движения полюса m и вращательного движения вокруг этого по-
люса с угловой скоростью ω (рис.8.4). При рассмат-
риваемом переносном движении вектор vотн пе-
реместиться вместе с кри- вой АВ поступательно, и
одновременно повернется вокруг точки m1 до поло-
z1
|
B |
В1 |
vотн |
d v отн 2 |
b1 |
b |
|
vотн v1отн
ω
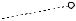 m1
m1
m
A A1
O1 |
y1 |
жения m1b1 . В результате x1
приращение вектора vотн в
переносном движении бу- |
Рис. 8.4 |
|
дет равно dvотн2 = bb1 = vb × dt ,
где vb - скорость, с которой перемещается точка b при повороте век- тора vотн . Так как этот поворот происходит с угловой скоростью ω ,
то vb = ω × m1b . Учитывая, что vотн = m1b , получим vb = ω ´ vотн .
Тогда dvотн2 = (ω ´ vотн ) × dt .
99

Разделив обе части равенства на dt, получим
|
|
|
|
|
|
|
|
|
|
dvотн2 |
= ω × vотн . |
|
|
|
|||
|
|
|
|
|
|
|
|
dvпер1 |
|
dt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теперь |
найдем |
|
|
. |
|
|
|
|
|
||||||||
|
|
dt |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При рассматриваемом пере- |
|
|
|
B v1пер |
|||||||||||||
носном |
движении |
скорость |
|
|
М1 |
|
dvпер1 |
||||||||||
любой точки на кривой АВ |
|
|
v |
||||||||||||||
будет равна |
vпер = vо + ω × r , |
z1 |
z |
|
пер |
||||||||||||
М m |
vпер |
||||||||||||||||
где vо = vm - скорость полю- |
|
r1 |
|||||||||||||||
са (рис.8.5). |
|
|
|
|
|
|
|
|
|
ω |
r |
y |
|
||||
|
|
|
времени |
|
|
|
|||||||||||
За промежуток |
|
O |
|
|
|
||||||||||||
dt точка совершит перемеще- |
|
|
|
A |
|
||||||||||||
ние vотнdt = |
MM1 |
. Новое по- |
|
x |
v0 |
|
|
||||||||||
ложение |
точки определяется |
O1 |
|
|
|
|
|||||||||||
радиус-вектором |
|
|
|
|
|
|
|
|
y1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r1 = r + MM1 . При этом новая |
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
скорость |
точки определяется x1 |
|
|
|
|
|
|||||||||||
как |
|
|
|
|
|
|
|
|
|
|
|
Рис.8.5 |
|
|
|
||
v1пер = vо + ω × (r + MM1) . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
Тогда приращение вектора переносной скорости вследствие относи-
тельного движения точки будет равно
dvпер1 = v1пер − vпер = vо + ω × (r + MM1) − vо − ω × r = .
= ω × MM1 = ω × vотнdt
Откуда dvпер1 = ω × vотн . dt
Таким образом, кориолисово ускорение равно удвоенному
векторному произведению переносной угловой скорости на относительную скорость точки.
акор = 2(ω × vотн ).
Модуль кориолисова ускорения определяется как модуль этого векторного произведения акор = 2ωперvотн sin α , где α – угол между
векторами ωпер и vотн .
Кориолисово ускорение равно нулю в трех случаях:
100
