§ 2.12 Двоично-кодированные счетчики с произвольным модулем.

В двоично-кодированных счетчиках с произвольным модулем модуль счета не равен целой степени числа два.

Разрядность такого счетчика определяется как , где- округление до ближайшего справа (большего) целого числа.

Такой счетчик имеет лишних состояний (неиспользуемых), которые подлежат исключению. Способов исключения таких состояний много.

Модуль такого счетчика может быть трех типов с точки зрения расположения на числовой оси:

Вид "а" – счет идет от 0 доК1 и модуль счета равен К1.

Вид "б" – счет идет от К1 до К2; M=K2–K1, число К1 устанавливается (записывается) в счетчик перед началом счета, по достижению числа К2 счетчик сбрасывается, считанный код требует перекодирования для естественного чтения.

Вид "в" – счет идет от К2 до 2ⁿ, М=2ⁿ–К1, К1 устанавливается перед началом счета, сброс счетчика – по окончанию счета автоматический; считанный код требует перекодирования.

Виды "б" и "в" применяются для построения специальных счетчиков.

Для построения счетчика с произвольным модулем используется два основных метода:

1. метод управляемого сброса

Сигналпоявляется как следствие появления в счетчике числаМ-1, т.к. входы И подключены к тем разрядам счетчика, которые определяют это число М-1.

Например: построить счетчик при М=10, тогда сигнал будет выработан при выходе.

Схема сброса предназначена для формирования сигнала сброса, удовлетворяющего требованиям входного сигнала сброса счетчика. В зависимости от этих требований этой схемы может и не быть.

Схемы разрядов счетчика с управляемым сбросом, как правило, не зависят от модуля счета.

2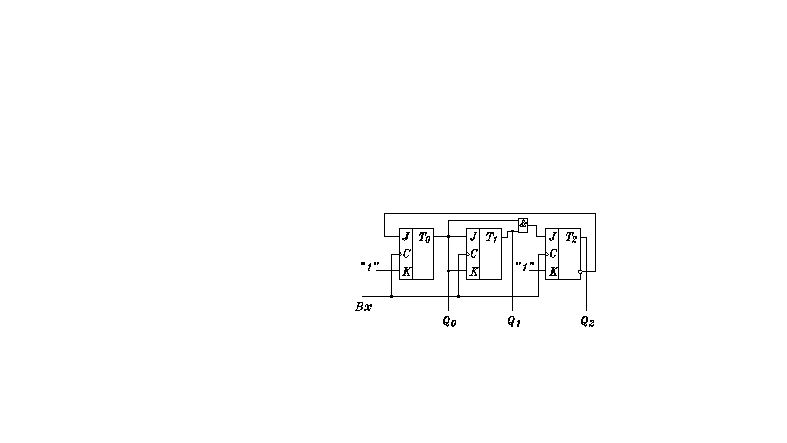)метод исключений лишних состояний с использованием определенных межразрядных связей счетчика

М=5

Лишние состояния: 101, 110, 111.

Пятым импульсом счетчик сбрасывается в ноль.

В рассмотренном счетчике при включении питания схемы (или при сбое в работе) схема может оказаться в одном из лишних состояний, но, благодаря ее свойству самовосстановления, схема приходит в рабочий цикл после начала работы.

§ 2.13 Счетчики с недвоичным кодированием.

Наибольшее распространение из этого класса счетчиков получили:

1) счетчики с кодом "1 из N"

2) счетчики на основе кольцевого регистра с перекрестной обратной связью (счетчик Джонсона, счетчик Мебиуса, счетчик Либау-Крейга)

3) счетчики с кодом Грея

1) Счетчик с кодом "1 из N" на базе сдвигающего регистра

В начале счета импульсом на входе "Уст 0" ТТ0-триггер устанавливается в единицу, а остальные триггеры – в ноль. Далее каждый импульс С переписывает эту единицу в следующий разряд, пока она не дойдет до Q_N-1.

Выходы счетчика считываются в десятичной системе счисления. С приходомС-импульса N-ая единица из Q_N-1 переписывается в ТТ0, и далее цикл повторяется.

Счетчики с кодом "1 из N" часто называют распределителями импульсов или тактов (РИ, РТ).

Недостаток счетчика: если в процессе работы появился сбой (например, возникла ложная единица), то она будет циркулировать в счетчике, выдавая тем самым ложный счет десятичной системе счисления на выходе.

Есть способы построения схемы с самовосстановлением (т.е. исправлением ошибки).

Счетчик "1 изN" можно построить на основе двоичного счетчика, если на его выход подключить дешифратор.

2) Счетчик Джонсона

По принципу построения ему аналогичны счетчик Мебиуса, счетчик Либау-Крейга.

Начальное состояние – ноль.

Первый импульсС установит Т1 в единицу (поскольку в это время равно единице); в остальных разрядах – нули, как результат сдвига нулей от соседних разрядов слева.

Второй импульс С сохраняет единицу в Т1 (т.к. все еще равно единице) и записы-

вает ее в Т2; в остальных разрядах – нули.

Последующие сдвиги приводят к заполнению единицами всех разрядов, т.е. пройдет "волна" единиц и в счетчике окажется записанной комбинация 1111.

Пятый импульс С установит Т1 в ноль (т.к. теперь =0). Далее пройдет "волна" нулей (с пятого по восьмой импульсы в счетчике комбинация – 0000).

Далее цикл повторяется.

Особенности схемы: при любом числе N разрядов число состояний счетчика равно 2N (т.е четное).

Полученный код представлен уровнями сигналов, поэтому его необходимо дешифровать или преобразовать. Принцип дешифровки основан на выявлении характерной временной координаты на диаграмме – это граница между зонами единиц и нулей.

№ сост-я	Q1	Q2	Q3	Q4	№ cост-я	Q1	Q2	Q3	Q4
0	0	0	0	0	4	1	1	1	1
1	1	0	0	0	5	0	1	1	1
2	1	1	0	0	6	0	0	1	1
3	1	1	1	0	7	0	0	0	1

В двух случаях (для слов 0000 и 1111) состояние счетчика выявляется анализом крайних разрядов. В остальных случаях анализируются разряды на границе единиц и нулей.

Тогда дешифровка в счетчике Джонсона может быть осуществлена по выражениям:

–выходное значение, которое должны получить

(i=0,1,2,3) – требуемые выходы дешифратора или распределителя

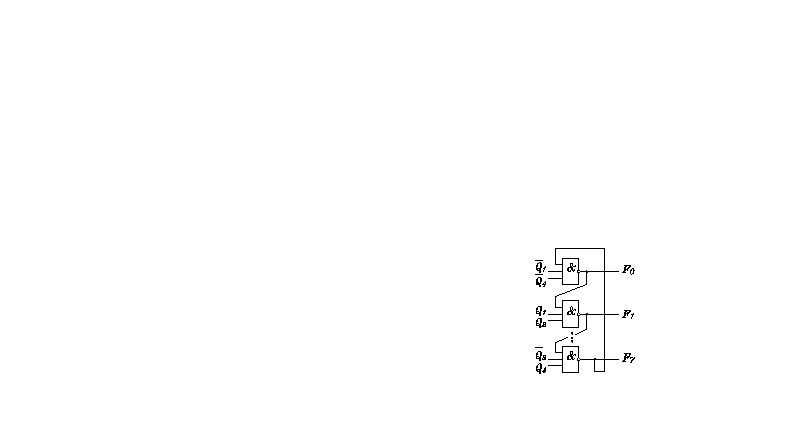
Временная

диаграмма:

Подсоединив входы полученной схемы к соответствующим выходам счетчика Джонсона, на выходах этой схемы получаем распределение импульсов или тактов.

Примечание:

1) В схеме счетчика всегда четное число состояний, если необходимо нечетное, то проблему можно решить исключением лишнего состояния одним из ранее рассмотренных способов.

В данной схеме это можно сделать так: например, исключить последнее состояние и перейти к следующему, т.е. осуществить переход не от 11…11, а от 11…10, которое создает единицу в предпоследнем разряде на прямом выходе и ноль – на инверсном.

Можно подать этот ноль на вход счетчика вместе с основным сигналом обратной связи через коньюнктор.

2) Схема счетчика Джонсона может попасть в одно из неиспользуемых состояний. Попадая в одно из этих состояний при сбое, счетчик может работать циклически в лишних состояниях.

Для придания свойств самовосстановления можно вырабатывать сигнал обратной связи, который восстановит нормальный цикл: .

3) Рассмотренные счетчики характеризуются небольшими аппаратными затратами: (½ триггера + элемент И) на каждый канал распределения.

Пример серийно-выпускаемых подобных счетчиков: К561ИЕ9, К561ИЕ19.