С другой стороны

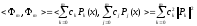
в силу ортогональности.

Подставляя в (8), получим

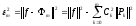. (9)

Пример 2.

Пусть f(x)=|x|.

Аппроксимировать f(x) на [-1,1] в среднеквадратичном многочленом второй степени. Вычислить среднеквадратичную ошибку.

Используем ортогональную систему Лежандра:

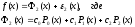
Коэффициенты c_k находим по формуле (7), учитывая вид полиномов Лежандра:

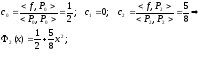
Далее вычисляем среднеквадратичную ошибку по формуле (9):

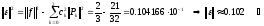
1.7. Некоторые общие свойства ортогональных полиномов.

1. Многочлен P_n(x) ортогонален любому алгебраическому многочлену m-ой степени M_m(x) при m<n.

M_m(x) можно единственным образом представить в виде линейной комбинации многочленов Лежандра:

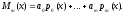(10)

Равенство (10) тождественное, поэтому коэффициенты a_k единственным образом вычисляются путем приравнивания коэффициентов при старших степенях. Умножая обе части (10) на P_n(x), имеем

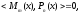
в силу ортогональности системы

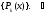
2. Полином P_n(x) имеет на отрезке [-1,1] ровно n действительных и различных корней.

Заметим, что в силу теоремы Гаусса многочлен P_n(x) не может иметь более чем n корней (вообще говоря, комплексных). Пусть P_n(x) имеет меньше, чем n простых действительных корней. Обозначим их 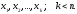По этим точкам построим фундаментальный многочлен

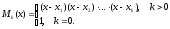
Рассмотрим многочлен: - многочлен степени (k+n), который имеет нули четной кратности. Значит, новый многочлен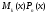сохраняет знак при переходе через эти нули, т.е. сохраняет знак на [-1,1]. Отсюда следует, что

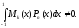
Но это противоречит свойству 1, так как P_n(x) обязательно должен быть ортогонален M_k(x).

3. Между двумя соседними нулями многочлена P_n(x) лежит ровно один нуль многочлена P_n-1(x).

Доказывается по индукции с помощью рекуррентного соотношения (6).

4. При n- четном многочлен P_n(x) – четная функция от x, при n- нечетном, P_n(x) – нечетная функция от x.

Лекция 5.

1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.

Определение.

На отрезке [-1,1] определим многочлены Чебышева:

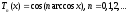(1)

Найдем несколько первых многочленов Чебышева по формуле (1):

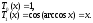
Далее используем формулу тригонометрии:

(2)

Полагая в (1) 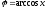и подставляя в (2), получаем:

(3)

Формула (3) – рекуррентная формула для полиномов Чебышева. Из (3) в частности следует, что 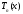- многочленn-ой степени. Последовательно получаем:

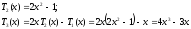
и т.д.

Свойства многочленов Чебышева.

1. Система ортогональна на отрезке [-1,1] с весом

.

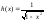Имеем:

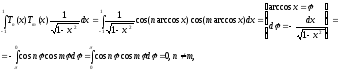
в силу ортогональности системы 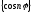на отрезке [0,].

Вычислим норму:

.

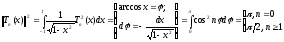2. Для четных (нечетных) n многочлен T_n(x) содержит только четные (нечетные) степени х, то есть является четной (нечетной) функцией.

Доказывается по индукции с помощью рекуррентной формулы (3).

3. Коэффициент при старшей степени xⁿ многочлена T_n(x) равен 2^n-1.

Доказывается по индукции с помощью рекуррентной формулы (3).

4. Многочлен T_n(x) имеет на интервале (-1, 1) ровно n различных действительных корней, определяемых формулой:

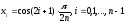(4)

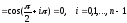
5. , причем максимум достигается в точках

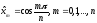(5)

При этом .

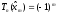Из определения (1) следует, что 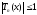для любого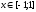. Очевидно, что.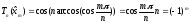

Замечание.

Нетрудно убедиться, что нули T_n(x) (формула (4)) и точки максимума 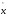полиномаT_n(x) (формула (5)) образуют чередующуюся последовательность, а именно:

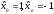, а для остальных значений: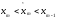, или

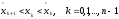
6. Многочлен 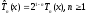среди всех многочленовn-ой степени с a_n=1

обладает тем свойством, что .

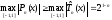Доказывается от противного: пусть существует 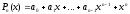, что

. (6)

Разность (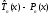) -многочлен (n-1)-ой степени, причем в силу (6) .

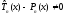Кроме того, заметим, что в силу (6) для .

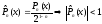Рассмотрим разность

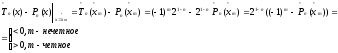
При переходе от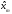к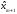разность меняет знак. Всего произойдетn раз смена знака

при переходе от точки 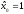к точке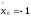.Отсюда следует, что многочлен 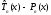имеетn нулей на (-1;1) , что невозможно, так как это многочлен (n-1)-ой степени.

Замечание.

Благодаря свойству (6) многочлен 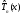называетсямногочленом наименее отклоняющимся от нуля.