3.3.Метод Ньютона.
Пусть снова задано уравнение
f(x)=0.
Запишем его в ви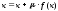де
,
где
и
.
Пусть
хк
– некоторое приближение к корню х*.
Для ускорения сходимости итераций
желательно, чтобы
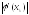был как можно меньше. Положим
,
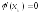то есть
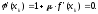
Отсюда находим, что
.
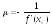Подставляя в исходное уравнение, получаем рекуррентную формулу:
.
Это и есть итерационная процедура Ньютона.
Лекция 10.
3.4. Численные методы линейной алгебры.
К численным методам линейной алгебры относятся: численные методы решения систем алгебраических уравнений (ЛАУ), обращение матриц, вычисление определителя матрицы, вычисление собственных значений и собственных векторов матриц.
Численные методы решения систем ЛАУ можно разбить на две группы: прямые методы (метод исключения Гаусса и его модификации) и так называемые итерационные методы.
Метод
Гаусса подробно рассматривается в курсе
линейной алгебры, где, в частности
показывается, что число арифметических
действий, затрачиваемых на приведение
системы к треугольному виду пропорционально
n3.
При вычислении определителя методом
Гаусса затрачивается
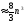арифметических действий.
Несмотря на очевидные преимущества прямых методов (конечность действий), их применение не всегда возможно. Если матрица A линейной системы плохо обусловлена, то вследствие неизбежных ошибок округления на ЭВМ, полученное приближенное решение системы может оказаться сколь угодно далеким от точного решения. Чтобы разобраться в этом вопросе, нам понадобится понятие нормы матрицы, спектра матрицы и обсудить некоторые дополнительные свойства матриц, связанные с этими понятиями.
3.4.1. Нормы матриц. Спектральные свойства матриц.
Пусть
,
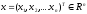Обозначим
Mn
- множество квадратных матриц
.
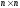Пусть
каждой матрице
поставлено в соответствие число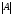
.
Это число называется нормой матрицы A, если выполняются следующие аксиомы:
1.
.
2.
.
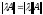3.
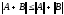(неравенство треугольника).
4.
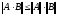(кольцевое свойство).
Определение.
Норма
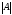называетсямультипликативной,
если выполняются все четыре аксиомы, и
аддитивной,
если выполняются первые три аксиомы.
Следствие.
Если норма матрицы A – мультипликативна, то согласно свойству 4:
.
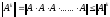Пусть
.
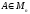Определим норму матрицы следующим
образом:
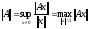. (1)
Таким
образом, определенная норма матрицы
называется подчиненной
векторной
норме
.
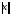Определение.
Если матричная норма удовлетворяет условию
, (2)
то такая норма называется согласованной с нормой вектора.
Следствие 1.
Любая подчиненная норма является также и согласованной (обратное вообще говоря, неверно).
Действительно,
из (1) в силу определения супремума:
,
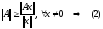Тот
факт, что обратное неверно, подтверждается
конкретными примерами матричных норм,
с которыми мы познакомимся далее.
Следствие 2.
Пусть
A=E
и норма матрицы – подчиненная векторной
норме. Тогда, поскольку Ex=x,
то
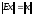и из (1) немедленно следует что
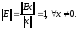
Полученное условие можно считать необходимым условием подчиненной нормы.
Определим некоторые наиболее употребительные на практике матричные нормы.
-
евклидова норма (норма Фробениуса:
norm(a, ‘fro’)-
в MATLAB),
-
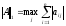“столбцовая” норма (norm(a,
1)),
-
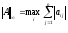“строчная” норма (norm(a,
inf)),
-
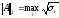“спектральная” норма (norm(a)=norm(a,
2)),
где
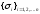- так называемыесингулярные
числа матрицы
А.
Пример 1.
Показать, что F – норма не является подчиненной векторной норме, если размерность матрицы такова, что n>1.
Имеем:
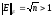приn>1.
И необходимое условие подчиненности
нормы нарушено.
Замечание.
Все
приведенные выше нормы матриц согласованы
с соответствующей нормой вектора.
Спектральная норма
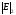является к тому же и подчиненной
евклидовой норме вектора. Кроме того,
среди всех возможных норм, согласованных
с евклидовой нормой вектора, спектральная
норма принимает минимальное значение.
Определение 1.
Число
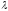(вообще говоря, комплексное) называется
собственным значением матрицыА,
соответствующим собственному вектору
x,
если выполняется условие:
. (3)
Определение 2.
Множество
всех собственных чисел матрицы А
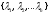, записанных с учетом их кратности,
называетсяспектром
матрицы А и
обозначается S(A).
Определение 3.
Спектральным
радиусом
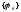квадратной матрицыА
называется максимальный из модулей ее
собственных значений.
Заметим, что система (3) эквивалентна следующей однородной системе уравнений:
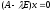. (4)
Как известно из курса линейной алгебры, система (4) имеет нетривиальные решения тогда и только тогда, когда
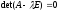. (5)
Уравнение
(5)- алгебраическое уравнение n-ой
степени относительно
.
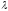Все его корни – собственные числа матрицы А.
Имеет место следующая
Теорема 1.