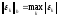- •Глава 1. Численные методы.
- •1.1 Структура погрешности в численном анализе.
- •Округление.
- •Погрешность вычисления функции при неточном задании аргументов. (Вопрос вычисления функции при наличии ошибки в вычислении ее аргумента)
- •1.2. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •1.3. Задача приближения функций. Интерполяция.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Общая задача интерполяции.
- •1.4. Интерполяционный многочлен Ньютона.
- •Пример:
- •Запись интерполяционного многочлена для равноотстоящих узлов.
- •1.5. Среднеквадратичное приближение функции.
- •1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •С другой стороны
- •1.7. Некоторые общие свойства ортогональных полиномов.
- •1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.
- •Первые применения многочленов Чебышева к задаче интерполяции.
- •1.9. Равномерное приближение функций на отрезке.
- •1.10 Теоремы о равномерном приближении функций на отрезке.
- •Глава II. Численное интегрирование.
- •2.1. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •2.2 Квадратурные формулы Гаусса-Кристоффеля.
- •Глава III. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3.Метод Ньютона.
- •3.4. Численные методы линейной алгебры.
- •3.4.1. Нормы матриц. Спектральные свойства матриц.
- •Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:
- •Простейшие следствия из определений.
- •3.4.2. Обусловленность матриц и систем уравнений.
- •3.4.3. Итерационные методы решения систем лау.
- •3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
- •Некоторые определения.
- •Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
- •4.1. Численное дифференцирование.
- •4.2.Численные методы решения задачи Коши.
- •4.2.1. Оценка погрешности метода Эйлера.
- •1. Ошибка растет с номером шага k.
- •4.2.2.Методы Рунге-Кутта.
- •4.3. Численные методы решения краевых задач для оду.
- •4.3.1.Задача аппроксимации на сетке.
- •4.3.2.Аппроксимация, устойчивость и сходимость разностных схем.
- •Итерационная процедура устойчива по правой части тогда и только тогда, когда
- •При этом, если выполняется условие
Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
Лекция 12.
4.1. Численное дифференцирование.
Различают 3 вида задач для обыкновенных дифференциальных уравнений (ОДУ): задача Коши, краевая задача и задача на собственные значения. В данной главе мы более подробно изучим численные методы решения задачи Коши.
Вначале приведем и обсудим формулы численного дифференцирования. Существует два подхода к выводу формул численного дифференцирования.
1. Интерполяционный подход.
Полагаем
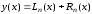 ,
,
где
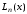 -
интерполяционный многочлен Лагранжа,
-
интерполяционный многочлен Лагранжа,
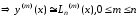 ,
,
причем
остаточный член формулы дифференцирования
выражается через
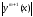
Недостаток:
при стремлении получить достаточно высокую точность приходится использовать большое количество узлов, в которых вычисляется значение функции. Если функция задана таблично, то такой подход приемлем.
2. Конечно-разностная аппроксимация, основанная на Тейлоровском разложении.
Рассмотрим этот подход более подробно.
Пусть
задана сетка
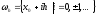 ,
где h - шаг сетки
,
где h - шаг сетки
Теорема 1.
Имеют место следующие утверждения:
Пусть
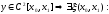
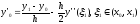 .
(1)
.
(1)
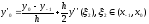 .
(2)
.
(2)
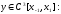
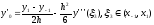 .
(3)
.
(3)

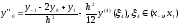 (4)
(4)
 Для
определенности докажем (4):
Для
определенности докажем (4):
используем тейлоровское разложение в точках x1 и x-1
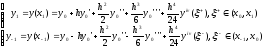 .
.
Складывая эти две формулы, получим
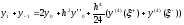 .
.
В
силу непрерывности четвертой производной


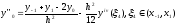 .
.
Замечание.
Формулы (1), (2), (3) и (4) называются формулами численного дифференцирования.
При этом
формула
(1) - определяет правую
разностную производную
и имеет порядок точности
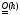 ,
,
формула
(2) – определяет левую
разностную производную и
имеет порядок точности
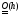 ,
,
формула
(3) - определяет центральную
разностную производную первого
порядка и имеет порядок точности
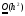 ,
,
формула
(4) - определяет центральную
разностную производную второго
порядка и имеет порядок точности
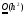 .
.
4.2.Численные методы решения задачи Коши.
Задача для ОДУ первого порядка для функции одной переменной ставится следующим образом
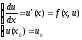 (5)
(5)
Более общая постановка задачи Коши для дифференциального уравнения n-го порядка
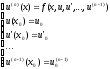 (6)
(6)
Здесь
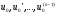 - заданные числа (начальные условия).
- заданные числа (начальные условия).
Задача (6) с помощью замены переменных
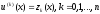 ,
,
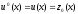 .
.
сводится к системе дифференциальных уравнений первого порядка:

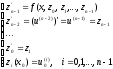 (7)
(7)
Систему (7) можно переписать в векторном виде:

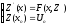 ,
где
,
где  (8)
(8)
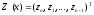 ,
,
 ,
,
 .
.
Система (8) исследуется и решается аналогично одномерной задаче Коши (5), поэтому важно изучить, прежде всего, численные методы решения задачи (5).
В
курсе математического анализа
формулируется и доказывается теорема
существования и единственности решения
задачи Коши. Отметим, что для выполнения
теоремы необходимо и достаточно, чтобы
функция
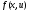 имела непрерывные частные производные
в замкнутой ограниченной области
имела непрерывные частные производные
в замкнутой ограниченной области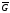 на плоскости
на плоскости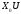 .
.
Будем
искать решение задачи (5) в прямоугольниках
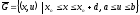
Введем
сетку на оси
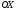
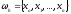 ,
,
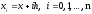

Простейший
итерационный процесс решения (5) на сетке
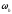 получается, если аппроксимировать
производную
получается, если аппроксимировать
производную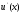 на сетке правой конечной разностью.
Обозначая приближенное решение на сетке
на сетке правой конечной разностью.
Обозначая приближенное решение на сетке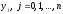 ,
получим
,
получим
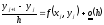
или
 (9)
(9)
Итерационная процедура (9) называется “метод Эйлера” (или “метод ломаных”).
Дадим графическую иллюстрацию метода.

Начав
движение из точки
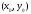 на точном решении
на точном решении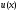 ,
итерационное решение образует ломаную
линию, каждый отрезок которой представляет
собой касательную к кривой
,
итерационное решение образует ломаную
линию, каждый отрезок которой представляет
собой касательную к кривой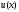 ,
проходящую через данную точку.
,
проходящую через данную точку.
Например,
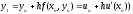 -
уравнение касательной к u(x)
в точке
-
уравнение касательной к u(x)
в точке
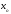 .
.
 где
u1(x1)-та
интегральная кривая, которая проходит
через точку (x1,y1).
где
u1(x1)-та
интегральная кривая, которая проходит
через точку (x1,y1).
Из
рисунка видно, что ошибка
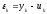 растет с
номером k. Выясним, каков порядок этой
ошибки в сеточной норме
растет с
номером k. Выясним, каков порядок этой
ошибки в сеточной норме