Итерационная процедура устойчива по правой части тогда и только тогда, когда
,
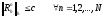где с не зависит от h (т.е. от N)
Однако, это условие не всегда легко проверить. Поэтому для конкретных итерационных схем вырабатываются и доказываются конкретные достаточные условия. Таковы, например, условия “благонеявного преобладания” для схем прогонки.
Теорема2.(Необходимый спектральный признак устойчивости).
Пусть
- собственные числа оператора Rh.
Для устойчивости схемы (8) по правой
части необходимо выполнение условия:
,
(9)
причем
константа
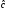не зависит от h (отN).
Пусть
(9) не выполняется для некоторого
собственного значения
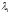.То есть, не существует
такой константы
,
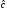для которой (9) выполнялось бы для данного
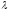.Фактически, это
означает, что вместо линейного ограничения
имеем:
,
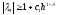где 0<<1,c1-некоторая
константа.
Пусть
- соответствующий собственный вектор,
т.е.
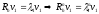
Оценим по сеточной норме:
.
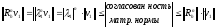Из последнего неравенства следует:
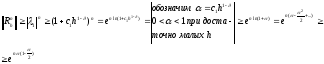
Заметим,
что
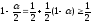по условию на ,
поэтому
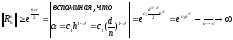
т.е.
нарушается условие устойчивости,
сформулированное ранее. Происходит
экспоненциальный рост ошибки.
Рассмотрим снова сеточное уравнение вида (6)
Теорема 3.(О сходимости разностной схемы (6)).
Пусть конечно-разностная задача (6) однозначно разрешима, аппроксимирует исходную дифференциальную задачу с порядком p относительно h и устойчива. Тогда имеет место сходимость:
,
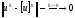где
-
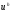решение сформулированной разностной
задачи;
-
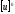точное решение дифференциальной задачи,
взятое на сетке.
При этом, если выполняется условие
,
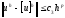то говорят, что имеет место сходимость порядка p.
Согласно
условию теоремы имеет место аппроксимация
порядка p:
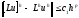(10)
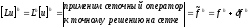(11)
-
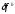невязка, которая получается при
подстановке точного решения в левую
часть уравнения. Подставляя в (10):
.
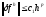(12)
В возмущенном уравнении
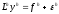
в
качестве возмущения выберем невязку,
т.е. положим
,
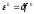тогда
. (13)
В силу старого определения устойчивости имеем:
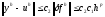. (14)
Уравнения (11) и (13) имеют одинаковые правые части. В силу однозначной разрешимости задачи (6), имеем:
,
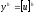подставим в (14)
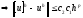
Таким образом, мы одновременно доказали сходимость и установили, что порядок сходимости совпадает с порядком аппроксимации.