
- •Глава 1. Численные методы.
- •1.1 Структура погрешности в численном анализе.
- •Округление.
- •Погрешность вычисления функции при неточном задании аргументов. (Вопрос вычисления функции при наличии ошибки в вычислении ее аргумента)
- •1.2. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •1.3. Задача приближения функций. Интерполяция.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Общая задача интерполяции.
- •1.4. Интерполяционный многочлен Ньютона.
- •Пример:
- •Запись интерполяционного многочлена для равноотстоящих узлов.
- •1.5. Среднеквадратичное приближение функции.
- •1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •С другой стороны
- •1.7. Некоторые общие свойства ортогональных полиномов.
- •1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.
- •Первые применения многочленов Чебышева к задаче интерполяции.
- •1.9. Равномерное приближение функций на отрезке.
- •1.10 Теоремы о равномерном приближении функций на отрезке.
- •Глава II. Численное интегрирование.
- •2.1. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •2.2 Квадратурные формулы Гаусса-Кристоффеля.
- •Глава III. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3.Метод Ньютона.
- •3.4. Численные методы линейной алгебры.
- •3.4.1. Нормы матриц. Спектральные свойства матриц.
- •Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:
- •Простейшие следствия из определений.
- •3.4.2. Обусловленность матриц и систем уравнений.
- •3.4.3. Итерационные методы решения систем лау.
- •3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
- •Некоторые определения.
- •Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
- •4.1. Численное дифференцирование.
- •4.2.Численные методы решения задачи Коши.
- •4.2.1. Оценка погрешности метода Эйлера.
- •1. Ошибка растет с номером шага k.
- •4.2.2.Методы Рунге-Кутта.
- •4.3. Численные методы решения краевых задач для оду.
- •4.3.1.Задача аппроксимации на сетке.
- •4.3.2.Аппроксимация, устойчивость и сходимость разностных схем.
- •Итерационная процедура устойчива по правой части тогда и только тогда, когда
- •При этом, если выполняется условие
1.4. Интерполяционный многочлен Ньютона.
Определение 1.
Пусть
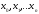 - сетка узлов,
- сетка узлов,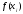 - значения функцииf(x)
в узлах
- значения функцииf(x)
в узлах
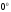 :
значения
:
значения
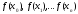 называютсяразделенными
разностями нулевого порядка
функции f(x).
называютсяразделенными
разностями нулевого порядка
функции f(x).
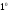 :
значения
:
значения
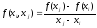 называются
разделенными разностями первого порядка
функции f(x).
называются
разделенными разностями первого порядка
функции f(x).
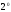 :
значения
:
значения
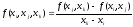 называютсяразделенными
разностями второго порядка
функции f(x).
называютсяразделенными
разностями второго порядка
функции f(x).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
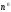 :
значения
:
значения
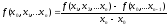 называются
разделенными разностями n–го порядка
функции f(x).
называются
разделенными разностями n–го порядка
функции f(x).
Простейшие свойства разделенных разностей.
f(x0, x1, …, xk) – симметричная функция своих аргументов, т.е. не меняется при любой перестановке аргументов.
 Заметим,
что любая разделенная разность есть
линейная функция своих аргуметов.
Заметим,
что любая разделенная разность есть
линейная функция своих аргуметов.
f(x0,
x1,
…, xk)
=
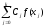 .
.
(устанавливается
по индукции) => результат.

Пример:
Установить вид коэффициентов Сj при фиксированном k.
 Самостоятельно.
Самостоятельно.
Если f(x)=Pn(x) – многочлен n-ой степени, то разделенные разности порядков (n+1) равны нулю.
 Заметим,
что Pn(x,
x0)
многочлен (n-1)-ой
степени,
Заметим,
что Pn(x,
x0)
многочлен (n-1)-ой
степени,
Pn(x, x0, x1) многочлен (n-2)-ой степени,
………………………………………………
Pn(x, x0, x1, …, x n-1) - многочлен 0-ой степени (т.е. const),
Pn(x, x0, x1, …, x n) 0.
………………………………………………

Рассмотрим многочлен n-ой степени вида
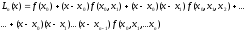 (9)
(9)
Теорема 3.
Многочлен
(9) является интерполяционным для f(x)
на сетке узлов
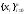 ,
т.е.
,
т.е.
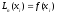 ,
i=0, 1,…, n (10)
,
i=0, 1,…, n (10)
 Рассмотрим разделенные разности
многочлена Лагранжа
Рассмотрим разделенные разности
многочлена Лагранжа
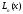 :
:
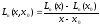 . (11)
. (11)
Числитель
в (11) – многочлен n
-ой степени, обращающийся в 0 в т.
 .
Следовательно, по теореме Безу числитель
в (11) делится без остатка на
.
Следовательно, по теореме Безу числитель
в (11) делится без остатка на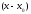 ,
а, следовательно,
,
а, следовательно,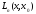 -многочлен (n-1)
-ой степени.
-многочлен (n-1)
-ой степени.
Из (11) находим
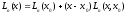 . (12)
. (12)
Далее
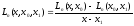 . (13)
. (13)
Числитель
в (13) – многочлен степени (n-1)
обращается в 0 при
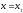 ,следовательно,
делится на
,следовательно,
делится на без остатка,
Ln
(x,
x0,
x1)
- многочлен (n-2)-ой
степени.
без остатка,
Ln
(x,
x0,
x1)
- многочлен (n-2)-ой
степени.
Из (12) с учетом (13) находим
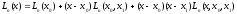 .
(14)
.
(14)
Продолжая таким же образом далее и учитывая, что (n+1) - ая разделенная разность
Ln(x, x0, …, xn) 0, окончательно находим
 (15)
(15)
Но
по условию теоремы
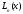 - интерполяционный многочлен дляf(x)
, т.е.
- интерполяционный многочлен дляf(x)
, т.е.
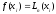 ,
i=0, 1,…, n
,
i=0, 1,…, n
Следовательно,
все разделенные разности для
 иf(x)
совпадают, поэтому (15) можно переписать
иf(x)
совпадают, поэтому (15) можно переписать
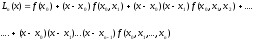 (16)
(16)
т.е.
получаем представление (9), что и
требовалось доказать. 
Замечание 1.
Мы
получили другую форму представления
интерполяционного многочлена Лагранжа.
Многочлен (9) называется интерполяционным
многочленом Ньютона
и обозначается также -
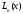 .
.
Замечание 2.
Интерполяционный
многочлен
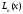 в форме Лагранжа содержит значения
в форме Лагранжа содержит значения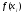 в явном виде. Это удобно, когда необходимо
построить интерполяционный многочлен
на тех же узлах, но для другой функции
–g(x).
Тогда значения
в явном виде. Это удобно, когда необходимо
построить интерполяционный многочлен
на тех же узлах, но для другой функции
–g(x).
Тогда значения
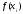 достаточно заменить на
достаточно заменить на .
.
Многочлен
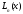 в форме Ньютона содержит
в форме Ньютона содержит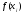 неявно (через разделенные разности).
неявно (через разделенные разности).
Однако, он удобен, когда для той же функции f(x) необходимо увеличить порядок n. Тогда к исходному многочлену достаточно добавить несколько членов стандартного вида.
