- •Глава 1. Численные методы.
- •1.1 Структура погрешности в численном анализе.
- •Округление.
- •Погрешность вычисления функции при неточном задании аргументов. (Вопрос вычисления функции при наличии ошибки в вычислении ее аргумента)
- •1.2. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •1.3. Задача приближения функций. Интерполяция.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Общая задача интерполяции.
- •1.4. Интерполяционный многочлен Ньютона.
- •Пример:
- •Запись интерполяционного многочлена для равноотстоящих узлов.
- •1.5. Среднеквадратичное приближение функции.
- •1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •С другой стороны
- •1.7. Некоторые общие свойства ортогональных полиномов.
- •1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.
- •Первые применения многочленов Чебышева к задаче интерполяции.
- •1.9. Равномерное приближение функций на отрезке.
- •1.10 Теоремы о равномерном приближении функций на отрезке.
- •Глава II. Численное интегрирование.
- •2.1. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •2.2 Квадратурные формулы Гаусса-Кристоффеля.
- •Глава III. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3.Метод Ньютона.
- •3.4. Численные методы линейной алгебры.
- •3.4.1. Нормы матриц. Спектральные свойства матриц.
- •Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:
- •Простейшие следствия из определений.
- •3.4.2. Обусловленность матриц и систем уравнений.
- •3.4.3. Итерационные методы решения систем лау.
- •3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
- •Некоторые определения.
- •Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
- •4.1. Численное дифференцирование.
- •4.2.Численные методы решения задачи Коши.
- •4.2.1. Оценка погрешности метода Эйлера.
- •1. Ошибка растет с номером шага k.
- •4.2.2.Методы Рунге-Кутта.
- •4.3. Численные методы решения краевых задач для оду.
- •4.3.1.Задача аппроксимации на сетке.
- •4.3.2.Аппроксимация, устойчивость и сходимость разностных схем.
- •Итерационная процедура устойчива по правой части тогда и только тогда, когда
- •При этом, если выполняется условие
3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
Пусть задана система ЛАУ общего вида (первого рода):
Ax=b;
x,b
 Rn,
Rn,
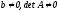 .(1)
.(1)
Требуется привести данную систему к виду
x=Tx+d (2)
с
матрицей (оператором) Т,
удовлетворяющей
условию
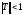 в какой либо матричной норме.
в какой либо матричной норме.
Рассмотрим простейший прием такого преобразования.
x=x-H(Ax-b), (3)
где Н- некоторая невырожденная матрица.
Из (3) следует, что
x=Tx+d, где (4)
T=E-HA, d=Hb.
Некоторые определения.
Итерационная процедура, основанная на представлении (3)
xk=xk-1-H(Axk-1-b) (5)
называется линейной стационарной итерационной процедурой; при этом матрица Т в представлении (4) называется матрицей перехода, а матрица Н – матрицей расщепления.
Более общая линейная нестационарная итерационная процедура записывается в виде:
xk= xk-1-Hk(A xk-1-b),
где Hk – матрица расщепления k-го шага.
Соответственно матрица перехода Tk=E-HkA – называется матрицей перехода k-го шага.
Ниже будут более подробно рассмотрены стационарные итерационные процедуры.
Связь условия сходимости линейного стационарного процесса со свойствами спектра матрицы Т устанавливает следующая теорема.
Теорема 1.
Пусть
система (4) имеет единственное решение
 стационарная процедура
стационарная процедура
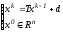 (6)
(6)
сходится
к решению системы (4) при
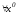 тогда и только тогда, когда все собственные
значения матрицыТ
по модулю меньше 1.
тогда и только тогда, когда все собственные
значения матрицыТ
по модулю меньше 1.
 Достаточность.
Достаточность.
Заметим,
что условие теоремы равносильно условию
 .
.
Пусть x* - точное (и единственное) решение системы (4). Запишем следующую систему:
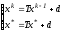
Вычитая из первого уравнения второе, получаем:
xk- x* = T(xk-1- x*).
Обозначим
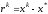 - ошибкаk-ого
шага. Тогда
- ошибкаk-ого
шага. Тогда
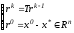 (7)
(7)
(7)
является итерационной процедурой для
операторного уравнения r=Tr,
достаточным
условием сходимости которой, согласно
принципу сжатых отображений, является
условие
 .
.
Заметим, что матрица Т- вещественная. Рассмотрим в качестве нормы матрицы Т- спектральную норму:
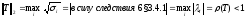 по
условию теоремы
по
условию теоремы
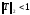 и
достаточность доказана.
и
достаточность доказана.
Необходимость.
От
противного. Пусть одно из собственных
значений матрицы Т,
например,
 и пустьy -
соответствующий
собственный вектор:
и пустьy -
соответствующий
собственный вектор:
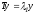 .
Выберем начальное приближение в виде
.
Выберем начальное приближение в виде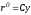 ,
гдеС -
некоторая
константа.
,
гдеС -
некоторая
константа.
Запустим итерационную процедуру:


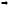 не
может быть нарушено условие
не
может быть нарушено условие
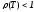 .
.
Рассмотрим некоторые частные случаи стационарных процедур, зависящих от выбора матрицы Н.
Пусть
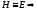 матрица
перехода в этом случае имеет вид:
матрица
перехода в этом случае имеет вид:
T=E-A.
Получаем так называемый метод простых итераций, или метод Ричардсона.
Выясним условия сходимости метода Ричардсона.
Пусть
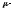 собственное
значение матрицыТ,
собственное
значение матрицыТ,
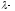 собственное значение матрицы А.
собственное значение матрицы А.
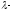 является
корнем характеристического уравнения
является
корнем характеристического уравнения
 ,
,
 корнем
уравнения
корнем
уравнения
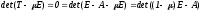
или:
 ,
откуда следует, что
,
откуда следует, что
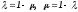 .
.
Согласно
теореме 1, условие сходимости:

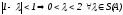
Последнее условие, например, выполняется, если
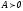 и
и
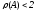 .
.
Пусть
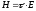 ,
где
,
где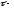 некоторый
параметр сходимости, с помощью которого
можно оптимизировать процедуру
Ричардсона.
некоторый
параметр сходимости, с помощью которого
можно оптимизировать процедуру
Ричардсона.
Матрица перехода в этом случае имеет вид:
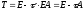 .
.
Теорема 2.
Пусть
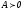 и
и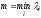 ,
,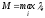

 является оптимальным значением параметра
сходимостиобобщенной
итерационной процедуры Ричардсона:
является оптимальным значением параметра
сходимостиобобщенной
итерационной процедуры Ричардсона:
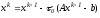 .
.
 Т.к.
Т.к.
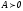 ,
то все
собственное значения матрицы А
,
то все
собственное значения матрицы А
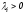
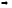 m, M>0 и
m, M>0 и
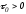 .
.
Выберем
в качестве матричной нормы - спектральную
норму
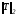 .
По определению,
.
По определению, ,
поэтому, чем меньше спектральный радиус,
тем быстрее сходится итерационная
процедура в соответствии с принципом
сжатых отображений.
,
поэтому, чем меньше спектральный радиус,
тем быстрее сходится итерационная
процедура в соответствии с принципом
сжатых отображений.
Пусть
 собственное значение матрицы
собственное значение матрицы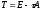
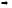
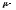 корень
уравнения
корень
уравнения
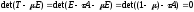
- корень уравнения:
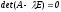
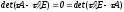
Из
сравнения двух характеристических
уравнений

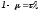

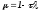
Таким образом, имеем:
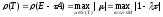 .
.
|
Так
как функция
|
|
Найдем
такое
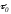 ,
для которого
,
для которого
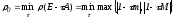 . (8)
. (8)
Легко
проверить, что при
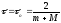 выполняются следующее условие:
выполняются следующее условие:
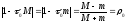 - обозначим.
- обозначим.
Покажем,
что полученное значение
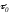 как раз и является оптимальным в смысле
критерия (8).
как раз и является оптимальным в смысле
критерия (8).
Пусть,
например,
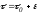

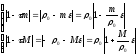 .
.
Из
последних равенств видно, что при любом
знаке
 один из модулей будет
один из модулей будет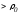 ,
т.е.
,
т.е.
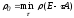 ,
,
что
и требовалось доказать.

Релаксационные методы.
В данном классе методов приведение системы (1) к виду (4) осуществляется с помощью расщепления матрицы А, т.е. ее представления в виде:
A=D-CL-CU , (9)
где
D= - диагональная матрица,
- диагональная матрица,
CL= - строго
нижняя (левая) треугольная матрица,
- строго
нижняя (левая) треугольная матрица,
CU= - строго
верхняя (правая) треугольная матрица.
- строго
верхняя (правая) треугольная матрица.
Подставляя
представление (9) в систему (1) Ax=b
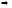
Dx=(CL+CU)x+b
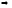
x=D-1(CL+CU)x+
D-1b
 x=Tx+d,
x=Tx+d,
где
T= D-1(CL+CU)= D-1(D-A)=E- D-1A,
d= D-1b,
H= D-1 - матрица расщепления.
Получаемый
при этом итерационный метод называется
методом
Якоби.
Необходимое условие сходимости:
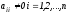 (иначе не существуетD-1).
(иначе не существуетD-1).
Достаточные условия сходимости в соответствии с теоремой 1:
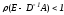 .
.
Или
более простое условие: пусть матрица А
- вещественная,
причем
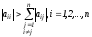 (такая
матрицаА
называется матрицей со строгим
диагональным преобладанием).
(такая
матрицаА
называется матрицей со строгим
диагональным преобладанием).
Метод Якоби может быть оптимизирован следующим образом. Снова воспользуемся разложением (9) и запишем систему в виде:
x=D-1CLx+ D-1CUx+d. (10)
Нетрудно убедиться, что при покомпонентной записи (10)
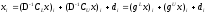 ,
где
,
где
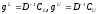
вектор
gLx
содержит только первые (i-1)
компонент вектора х
, а вектор
gUx
- содержит
компоненты, начиная с (xi+1)

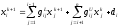 .
(11)
.
(11)
Процедура (11) носит название итерационный метод Гаусса-Зейделя
Условия сходимости - те же, что и для метода Якоби, но при этом получается дополнительное ускорение процедуры. Более эффективное ускорение сходимости метода Зейделя может быть достигнуто с помощью ускоряющего множителя (как в обобщенном методе Ричардсона). Получающийся при этом алгоритм носит название “метод последовательной верхней релаксации” и реализуется в два этапа:
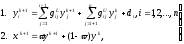 (12)
(12)
где
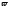 -релаксационный
параметр. Если
-релаксационный
параметр. Если
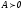 ,
то при
,
то при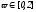 итерационная процедура сходится.
итерационная процедура сходится.

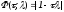 кусочно
линейна по,
то
кусочно
линейна по,
то
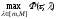 достигается на концах отрезка
достигается на концах отрезка