Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:

Пусть-произвольное собственное значение матрицы A, и - соответствующий собственный вектор.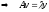

Оценим по норме:

Определение 4.

Сингулярным числом матрицыА называется собственное значение матрицы .

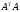Определение 5.

Матрица А называется положительно (неотрицательно) определенной (пишут: 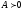или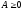), если соответствующая квадратичная форма

.

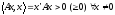Простейшие следствия из определений.

Следствие 1. Критерий Сильвестра:

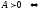все ведущие угловые миноры матрицы А положительны.

Следствие 2.

, причем .

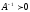следует из критерия Сильвестра

Следствие 3.

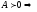все собственные значения .

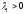Пусть - собственное значение, соответствующее собственному векторуx.

По условию 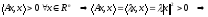результат.

Следствие 4.

Пусть А – вещественная матрица 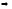матрица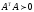

Имеем: 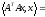{по свойству скалярного произведения}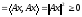

Следствие 5.

Сингулярные числа вещественной матрицы А – неотрицательны

Следует из С3 и С4.

Следствие 6.

Пусть А – вещественная матрица .

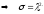Имеем:

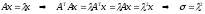
Следствие 7.

Если А – невырожденная матрица 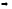собственные значения матрицА и A^-1 взаимообратны.

Пусть результат.

3.4.2. Обусловленность матриц и систем уравнений.

Пусть дана система ЛАУ с невырожденной матрицей А :

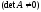Ax=b, (6)

и пусть вектор правой части b вычисляется с ошибкой .

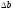Заменим правую часть “возмущенным” значением 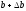, тогда решение приобретет ошибку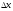и система примет вид:

. (7)

Оценим относительную ошибку решения в зависимости от относительной величины возмущения правой части.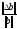

Из (6) и (7) следует:

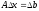
или

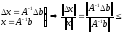{согласованность матриц}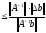(8)

С другой стороны, из (6) следует

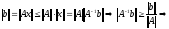подставим в (8)

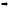
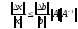. (9)

Определение 6.

Число называетсячислом обусловленности матрицы А.

Таким образом, из (9) следует, что максимальная относительная ошибка решения пропорциональна числу обусловленности матрицы А:

.

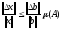Если 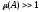(система уравненийплохо обусловлена), то небольшие погрешности вычисления правой части (небольшие “возмущения”) могут приводить к весьма большим отклонениям от точного решения.

Заметим, что это явление не связано с явлением неустойчивости (т.е. накоплением ошибок при вычислениях), а является следствием специфического свойства матрицы А и наблюдается даже в том случае, когда все вычисления делаются абсолютно точно, а возмущение правой части вызвано неточностями начальных данных при формировании системы. На семинаре и лабораторной работе будут рассмотрены примеры плохо обусловленных систем.

3.4.3. Итерационные методы решения систем лау.

Рассмотрим вначале систему ЛАУ вида

x=Tx+d, 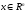,T- матрица 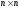(10)

Назовем эту систему системой “второго рода”, в отличии от вида системы (1) – системы “первого рода”.

Систему второго рода (10) естественно пытаться решать итерационным методом

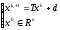, k=0,1,….. (11)

В этом методе используются лишь операции сложения и умножения, и не используется операция деления – наиболее опасная для накопления ошибок.

Очевидно, что оператор Т - линейный и отображает Rⁿ в себя.

Тогда согласно У2 из лекции 10, если для какой-либо из матричных норм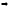выполняются условия теоремы 1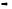существует единственная неподвижная точкаx^* оператора Т, удовлетворяющая системе

x*=Tx*+d, (12)

причем процедура (11) сходится к точке x^* со скоростью геометрической прогрессии.

Действительно, из (11) и (12)

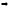
x^k+1-x^*=T(x^k-x^*)={продолжая рекурсию}=…=T^k(x⁰-x^*)

Оценивая по норме, получаем:

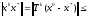{согласованность+мультипликативность матричной нормы}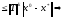прирезультат: сходимость с линейной скоростью.

Лекция 11.