Запись интерполяционного многочлена для равноотстоящих узлов.

Пусть 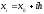,h>0, i=0, …, n

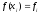
Определение 2.

1. Величин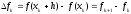а называетсяконечной разностью первого порядка.

2.

Величина

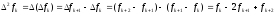
называется конечной разностью второго порядка.

. . . . . . . . . . . . . . . .

n. Величин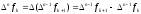а называетсяконечной разностью n-го порядка.

Лемма 1.

Для равноотстоящих узлов между разделенными и конечными разностями существует следующая связь:

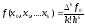, k = 0, 1, … (17)

По индукции:

k=0 – очевидно;

k=1

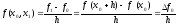- верно.

Пусть (17) установлено для номера k. Докажем, что тогда оно верно и для номера (k+1).

(k+1):

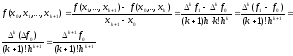
Т.о., установлено, что (17) верно для k{0, 1, …,n}.

Лемма 2.

Пусть задана сетка равноотстоящих узлов на отрезке [a,b]:

a  x₀ < x₁ <…< x_n < x_n+1  b, x_k = x₀ + hk, k = 0, 1, …, n+1

и .

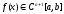Тогда существует точка 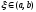такая, что

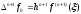(18)

По индукции:

k=1:

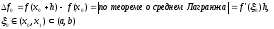
k=2:

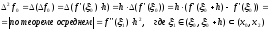
………………………………… и т.д.

k=n+1:

.

Установим теперь вид многочлена Ньютона для равноотстоящих узлов.

Введем переменную 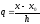. Очевидно, что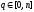, если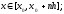

x-x_k=h(q-k), k = 0, 1, …, n.

В формуле полинома Ньютона (9) выразим все разности (x-x_k) через q и все разделенные разности по формуле (17):

(19)

Оценим погрешность формулы Ньютона (19).

Из формул остаточного члена (4) и (5) с учетом леммы 2, следует

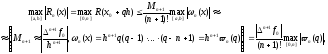
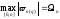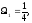
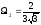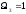, ,и так далее.

Земечание.

Интерполяционную формулу (19) применяют на практике для точек x, близких к x₀. Если необходимо вычислить приближенное значение функции f(x) в точках x, близких к правому концу отрезка, то полагают 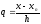и записывают интерполяционный многочлен Ньютона в терминах данногоq.

Пример .

Записать выражение многочлена Ньютона для данного случая.

Самостоятельно.

Лекция 4.

1.5. Среднеквадратичное приближение функции.

Рассмотрим задачу наилучшего среднеквадратичного приближения функции 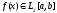полиномом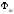по системе.

Определение 1.

Обобщенным полиномом порядка m по системе {_k} называется линейная комбинация

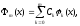
где C_k – произвольные вещественные коэффициенты.

Задача. Найти полином 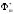, наименее уклоняющийся от функцииf в метрике L₂, т.е. удовлетворяющий условию:

Теорема 1.

Если систе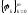ма линейно независима, то задача наилучшего среднеквадратичного приближения по этой системе однозначно разрешима.

Запишем квадрат расстояния между функцией и полиномом:

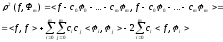(1)

Очевидно, что величина 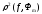- неотрицательно определенная квадратичная функция переменных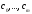, а такая функция достигает минимального значения. Таким образом, решение задачи среднеквадратичного приближения существует.

Докажем единственность решения.

Запишем необходимые условия минимума:

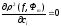, i=0,…,m.

Вычисляя частные производные по c_i выражения (1), получим линейную cистему уравнений:

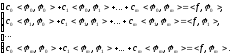(2)

Система (2) называется нормальной системой.

Выпишем определитель этой системы

(3)

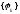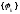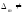Определитель системы (3) – так называемый определитель Грама системы . Известно, что если система- линейно независима, то определитель0 (легко доказывается от противного). Согласно условию теоремы0 и система (2) имеет единственное решение.