
- •Глава 1. Численные методы.
- •1.1 Структура погрешности в численном анализе.
- •Округление.
- •Погрешность вычисления функции при неточном задании аргументов. (Вопрос вычисления функции при наличии ошибки в вычислении ее аргумента)
- •1.2. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •1.3. Задача приближения функций. Интерполяция.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Общая задача интерполяции.
- •1.4. Интерполяционный многочлен Ньютона.
- •Пример:
- •Запись интерполяционного многочлена для равноотстоящих узлов.
- •1.5. Среднеквадратичное приближение функции.
- •1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •С другой стороны
- •1.7. Некоторые общие свойства ортогональных полиномов.
- •1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.
- •Первые применения многочленов Чебышева к задаче интерполяции.
- •1.9. Равномерное приближение функций на отрезке.
- •1.10 Теоремы о равномерном приближении функций на отрезке.
- •Глава II. Численное интегрирование.
- •2.1. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •2.2 Квадратурные формулы Гаусса-Кристоффеля.
- •Глава III. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3.Метод Ньютона.
- •3.4. Численные методы линейной алгебры.
- •3.4.1. Нормы матриц. Спектральные свойства матриц.
- •Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:
- •Простейшие следствия из определений.
- •3.4.2. Обусловленность матриц и систем уравнений.
- •3.4.3. Итерационные методы решения систем лау.
- •3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
- •Некоторые определения.
- •Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
- •4.1. Численное дифференцирование.
- •4.2.Численные методы решения задачи Коши.
- •4.2.1. Оценка погрешности метода Эйлера.
- •1. Ошибка растет с номером шага k.
- •4.2.2.Методы Рунге-Кутта.
- •4.3. Численные методы решения краевых задач для оду.
- •4.3.1.Задача аппроксимации на сетке.
- •4.3.2.Аппроксимация, устойчивость и сходимость разностных схем.
- •Итерационная процедура устойчива по правой части тогда и только тогда, когда
- •При этом, если выполняется условие
2.2 Квадратурные формулы Гаусса-Кристоффеля.
Рассмотрим
общую задачу численного интегрирования
с весовой функцией
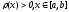 .
При построении квадратурных формул
интерполяционного типа необходимо
ввести дополнительно условие на весовую
функцию:
.
При построении квадратурных формул
интерполяционного типа необходимо
ввести дополнительно условие на весовую
функцию:
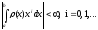 (1)
(1)
Запишем
квадратурную формулу для произвольного,
но фиксированного распределения узлов
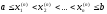 :
:
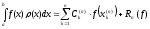 .
(2)
.
(2)
При
построении квадратурных формул
Ньютона-Котеса узлы
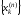 распределялись равномерно по отрезку
[a,b].
Очевидно, что такой способ выбора узлов
становится невозможным для несобственных
интегралов с бесконечными пределами.
распределялись равномерно по отрезку
[a,b].
Очевидно, что такой способ выбора узлов
становится невозможным для несобственных
интегралов с бесконечными пределами.
Возникает вопрос: как выбрать систему узлов квадратурной формулы, чтобы формула (2) имела наивысшую возможную алгебраическую степень точности?
Напомним,
что квадратурная формула имеет
алгебраическую степень точности
 ,
если она точна для многочленов степени
меньшей или равной
,
если она точна для многочленов степени
меньшей или равной .
.
Заметим, что формула (2) содержит всего 2n неизвестных параметров (n узлов и n весовых коэффициентов). Столько же коэффициентов содержит и произвольный многочлен степени 2n-1.
Таким образом, наивысшая алгебраическая степень точности формулы (2) не может быть больше 2n-1.
Определение 1.
Квадратурная формула (2), обеспечивающая условие:
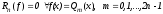
называется квадратурной формулой наивысшей алгебраической степени точности.
Теорема 1.
Пусть
{Pk(x)},
k=0,1,…, -
система ортогональных с весом
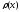 многочленов на [a,b].
многочленов на [a,b].
Для
того чтобы формула (2) была квадратурной
формулой наивысшей алгебраической
степени точности, необходимо и достаточно,
чтобы узлы
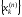 совпадали с нулями многочленаPn(x).
При этом такая квадратурная формула -
единственная.
совпадали с нулями многочленаPn(x).
При этом такая квадратурная формула -
единственная.
 Необходимость.
Необходимость.
Из
теории ортогональных многочленов
известно, что при выполнении условия
(1) на весовую функцию, существует полная
ортогональная на [a,b]
c весом
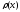 система алгебраических многочленов
система алгебраических многочленов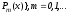 :
:
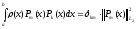 , (3)
, (3)
где
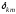 -
символ Кронекера.
-
символ Кронекера.
При
этом все нули многочлена Pn(x)
при
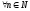 действительны
и расположены на [a,b].
действительны
и расположены на [a,b].
Как и при выводе интерполяционных формул, обозначим
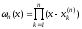 -
полином n-ой
степени, нули которого совпадают с
узлами интерполяции.
-
полином n-ой
степени, нули которого совпадают с
узлами интерполяции.
Рассмотрим
функцию
 .
Так как
.
Так как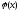 - алгебраический многочлен степени
- алгебраический многочлен степени ,
то по условию теоремы формула (2) - точна,
т.е.
,
то по условию теоремы формула (2) - точна,
т.е.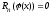 .
Но т.к.
.
Но т.к.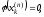 то из (2)
то из (2)
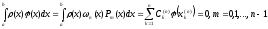
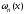 ортогональна
системе
ортогональна
системе
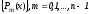

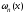 лишь коэффициентом при старшей степени
отличается от многочлена
лишь коэффициентом при старшей степени
отличается от многочлена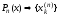 -
являются нулями полиномаPn(x).
-
являются нулями полиномаPn(x).
Достаточность.
Пусть
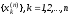 - нули полиномаPn(x),
и
- нули полиномаPn(x),
и
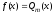 - полином степени
- полином степени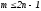 .
Требуется доказать, что
.
Требуется доказать, что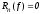 для
для .
.
Достаточно
рассмотреть случай
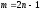 (если
формула точна для многочлена степени
(если
формула точна для многочлена степени ,
то она автоматически точна и для
многочлена любой меньшей степени).
,
то она автоматически точна и для
многочлена любой меньшей степени).
Пусть
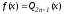 .
Представим этот многочлен в виде:
.
Представим этот многочлен в виде:
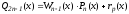 ,
(4)
,
(4)
где
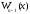 -
многочлен
-
многочлен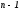 -ой
степени (частное от деления
-ой
степени (частное от деления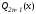 на
на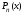 ),
), ,
,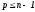 -
многочленр-ой
степени (остаток от деления).
-
многочленр-ой
степени (остаток от деления).
Т.к.
 - нули полинома
- нули полинома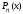 ,
то из (4) следует, что
,
то из (4) следует, что
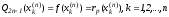 ,
,
т.е.
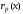 является интерполяционным многочленом
для
является интерполяционным многочленом
для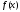 :
:
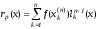 , (5)
, (5)
где
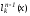 - фундаментальный многочлен Лагранжа
- фундаментальный многочлен Лагранжа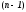 -
степени.
-
степени.
Учитывая (4) и (5), распишем интеграл:
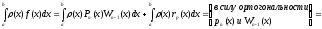
=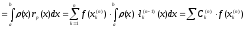 (6)
(6)
Формула
(6) - квадратурная формула интерполяционного
типа, причем
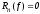 для
для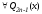 и, значит, и для любого многочлена
степени, меньшей или равной
и, значит, и для любого многочлена
степени, меньшей или равной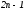 .
.
Единственность
квадратурной формулы (2) следует из
единственности выражений для нулей
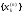 ортогонального
полиномаPn(x).
ортогонального
полиномаPn(x).
Определение 2.
Квадратурная
формула (6) наивысшей алгебраической
степени точности носит название формулы
Гаусса-Кристоффеля,
а весовые коэффициенты
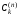 -коэффициенты
Кристоффеля.
-коэффициенты
Кристоффеля.
Теорема 2.
Весовые коэффициенты Кристоффеля удовлетворяют следующим условиям:
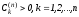 ,
,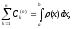
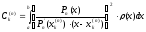 .
(7)
.
(7)
 По
доказанному в теореме 1, формула (6) точна
для многочленов порядка
По
доказанному в теореме 1, формула (6) точна
для многочленов порядка
 ,
в частности, для
,
в частности, для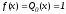
 - свойство (2).
- свойство (2).
Возьмем
в качестве
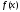 полином степени
полином степени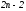 :
:
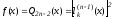 ,
где
,
где - произвольный номер, а
- произвольный номер, а - фундаментальный многочлен Лагранжа,
построенный по нулям
- фундаментальный многочлен Лагранжа,
построенный по нулям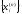 многочлена
многочлена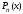 .
Учитывая свойства многочленов
.
Учитывая свойства многочленов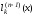
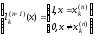 ,
получим из (6):
,
получим из (6):
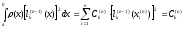 .
.
Из
последнего равенства следует, в
частности, что
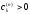 (свойство 1)). Кроме того заметим, что
(свойство 1)). Кроме того заметим, что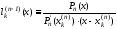 ,
т.к. эти два полинома имеют одну и ту же
степень, коэффициент при старшей степени
равен 1, и имеют одни и те же нули
,
т.к. эти два полинома имеют одну и ту же
степень, коэффициент при старшей степени
равен 1, и имеют одни и те же нули на отрезке
на отрезке
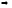 формула (7), т.е. свойство 3) доказано.
формула (7), т.е. свойство 3) доказано.
Замечание 1.
Для остаточного члена квадратурной формулы Гаусса-Кристоффеля справедливо представление:
 (8)
(8)
где
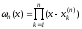 ,
, - нули полинома
- нули полинома ,(a,b).
,(a,b).
 Без
доказательства.
Без
доказательства.

Замечание 2.
Классические
ортогональные многочлены обычно строятся
для канонических промежутков:
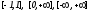 с соответствующими весами
с соответствующими весами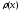 .
Если
.
Если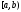 - конечный промежуток, то его с помощью
линейного преобразования
- конечный промежуток, то его с помощью
линейного преобразования
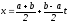 .
.
приводим
к отрезку
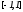 (
(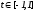 ).
При этом:
).
При этом:
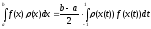 .
.
Приведем основную сводку квадратурных формул Гаусса-Кристоффеля для основных канонических промежутков.
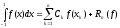 ,
,

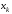 - нули полиномов Лежандра
- нули полиномов Лежандра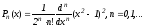
Рекуррентные соотношения:

 ;
или
;
или
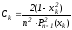 ,
, ,
,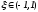 .
.
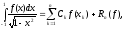
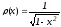 ,
,
 ,
,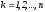 - нули полинома Чебышева
- нули полинома Чебышева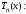
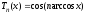
Рекуррентные соотношения:
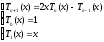
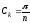 ,
,
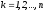
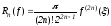 ,
,
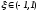
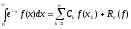 ,
,
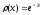
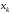 -
нули полинома
Лагерра
-
нули полинома
Лагерра
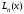 .
.
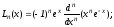
Рекуррентные соотношения:
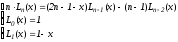
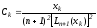 ,
,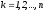
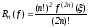 ,
,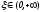
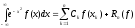 ,
,
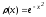 ;
;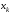 - нулиполинома
Эрмита
- нулиполинома
Эрмита
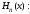
 .
.
Рекуррентные соотношения:

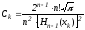 ,
,
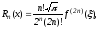
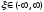 .
.
Пример 1.
Вычисляется
интеграл
 с помощью квадратурной формулы
Гаусса-Кристоффеля порядка
с помощью квадратурной формулы
Гаусса-Кристоффеля порядка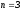 .
Оценить по модулю остаточный член
.
Оценить по модулю остаточный член .
.
 Согласно
случаю 2) из таблицы:
Согласно
случаю 2) из таблицы:
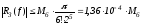 ,
где
,
где
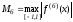 .
.
Пример 2.
Вычисляется
интеграл
 с помощью квадратурной формулы
Гаусса-Кристоффеля порядка
с помощью квадратурной формулы
Гаусса-Кристоффеля порядка .
Оценить по модулю
.
Оценить по модулю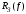 и указать саму формулу.
и указать саму формулу.

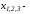 нули
многочлена Лежандра
нули
многочлена Лежандра
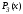 .
Согласно таблице (случай 1),
.
Согласно таблице (случай 1),

 ,
,
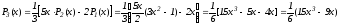 .
.
Найдем нули полинома

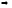
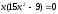
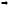
 ,
,
 ,
, .
.
Найдем
 ,
,
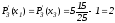 ,
,
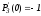 .
.
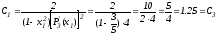 ,
,

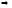
 ,
,
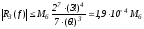 .
.

