
- •Глава 1. Численные методы.
- •1.1 Структура погрешности в численном анализе.
- •Округление.
- •Погрешность вычисления функции при неточном задании аргументов. (Вопрос вычисления функции при наличии ошибки в вычислении ее аргумента)
- •1.2. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •1.3. Задача приближения функций. Интерполяция.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Общая задача интерполяции.
- •1.4. Интерполяционный многочлен Ньютона.
- •Пример:
- •Запись интерполяционного многочлена для равноотстоящих узлов.
- •1.5. Среднеквадратичное приближение функции.
- •1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •С другой стороны
- •1.7. Некоторые общие свойства ортогональных полиномов.
- •1.8. Многочлены Чебышева, их свойства и применение в задачах приближения функций.
- •Первые применения многочленов Чебышева к задаче интерполяции.
- •1.9. Равномерное приближение функций на отрезке.
- •1.10 Теоремы о равномерном приближении функций на отрезке.
- •Глава II. Численное интегрирование.
- •2.1. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •2.2 Квадратурные формулы Гаусса-Кристоффеля.
- •Глава III. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3.Метод Ньютона.
- •3.4. Численные методы линейной алгебры.
- •3.4.1. Нормы матриц. Спектральные свойства матриц.
- •Для любой квадратной матрицы и любой согласованной матричной нормы имеет место неравенство:
- •Простейшие следствия из определений.
- •3.4.2. Обусловленность матриц и систем уравнений.
- •3.4.3. Итерационные методы решения систем лау.
- •3.4.4 Стационарные итерационные процедуры. Теоремы о сходимости.
- •Некоторые определения.
- •Глава IV. Численные методы решения обыкновенных дифференциальных уравнений.
- •4.1. Численное дифференцирование.
- •4.2.Численные методы решения задачи Коши.
- •4.2.1. Оценка погрешности метода Эйлера.
- •1. Ошибка растет с номером шага k.
- •4.2.2.Методы Рунге-Кутта.
- •4.3. Численные методы решения краевых задач для оду.
- •4.3.1.Задача аппроксимации на сетке.
- •4.3.2.Аппроксимация, устойчивость и сходимость разностных схем.
- •Итерационная процедура устойчива по правой части тогда и только тогда, когда
- •При этом, если выполняется условие
Глава II. Численное интегрирование.
Лекция 7.
2.1. Квадратурные формулы на основе интерполяций.
Пусть
требуется вычислить интеграл:
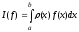 , (1)
, (1)
где
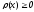
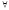
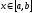 -весовая
функция
-весовая
функция
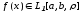 (
абсолютно интегрируема на
(
абсолютно интегрируема на
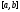 с весом (x))
с весом (x))
Рассмотрим
сначала случай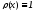 .
.
Определение.
Квадратурной формулой n-го порядка для интеграла (1) называется выражение вида:
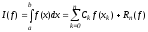 , (2)
, (2)
где
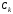 -
веса квадратурной формулы,
-
веса квадратурной формулы,
 -
узлы ,
-
узлы ,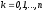 (
(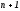 узел),
узел), -остаточный
член квадратурной формулы.
-остаточный
член квадратурной формулы.
Начнем с рассмотрения простого примера.
Пример 1.
Пусть
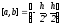 ,
,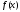 -
строго выпукла на этом отрезке,
-
строго выпукла на этом отрезке,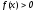 ,(
,( ).Заменим
).Заменим константой на
константой на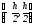 .
Как ее выбрать? (т.е. приблизить функцию
полиномом нулевой степениQ0(x)).
.
Как ее выбрать? (т.е. приблизить функцию
полиномом нулевой степениQ0(x)).
1)
Положим
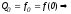 см. рисунок. Площадь
см. рисунок. Площадь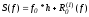 -формула
прямоугольника.
-формула
прямоугольника.
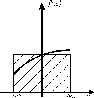
2)
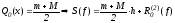 -
что лучше?
-
что лучше?
3)
Выберем
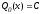 таким образом, чтобы
таким образом, чтобы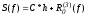 ,
причем
,
причем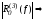 min
в классе функций.
min
в классе функций.
Первый подход связан с приближением функции интерполяционным многочленом. Это наиболее простой путь получения квадратурных формул. Рассмотрим этот подход наиболее подробно.
Положим
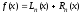 , (3)
, (3)
где
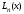 -
многочлен Лагранжа, построенный по
узлам
-
многочлен Лагранжа, построенный по
узлам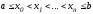 ,
выбираемых пока произвольно. Как известно
из теории интерполяции (Л-2)
,
выбираемых пока произвольно. Как известно
из теории интерполяции (Л-2)
 ,
где (4)
,
где (4)
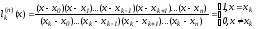 (5)
(5)
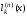 -
фундаментальные полиномы Лагранжа.
-
фундаментальные полиномы Лагранжа.
Остаточный член интерполяционной формулы имеет вид (Л-2):
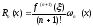 ,
,
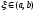
где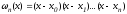
Из
(3) и (4)
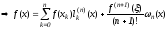 (6)
(6)
Проинтегрируем
формулу (6) по
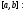
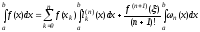


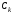
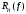
Обозначим
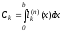 ,
,
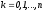 (7)
(7)
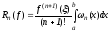 (8)
(8)
(7)-веса, (8)-остаточный член квадратурной формулы, интегралы в (7) легко вычисляются, как интегралы от полиномов. Рассмотрим некоторые частные случаи.
n=0
Нужна
одна точка (узел)
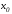 .
.
Если
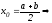 используя формулы (5) и (7), получим формулу
прямоугольников типа 1) из примера 1.
Заметим, что исследование остаточного
члена в виде (8) не совсем удобно, так
как необходимо уточнить точку
используя формулы (5) и (7), получим формулу
прямоугольников типа 1) из примера 1.
Заметим, что исследование остаточного
члена в виде (8) не совсем удобно, так
как необходимо уточнить точку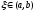 ,
которая определяется в соответствии с
теоремой о среднем. Будем оценивать
остаточный член по модулю:
,
которая определяется в соответствии с
теоремой о среднем. Будем оценивать
остаточный член по модулю:
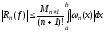 ,
(9)
,
(9)
где
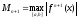 .
.
Пример.
Получить оценку остаточного члена для формулы прямоугольников.
 Самостоятельно.
Самостоятельно.
Перейдем к выводу квадратурной формулы порядка 1.
n=1
Узлы:
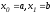 .Согласно формулам
(5), имеем
.Согласно формулам
(5), имеем
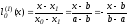
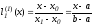
По
формуле (7)

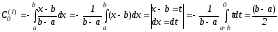
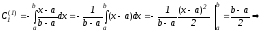
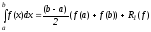 –формула
трапеций
–формула
трапеций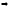 (10)
(10)
Площадь под кривой y=f(x) приближается с помощью формулы
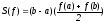 -
площадь трапеции.
-
площадь трапеции.
Геометрическая иллюстрация.
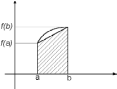
Оценим остаточный член формулы трапеций:
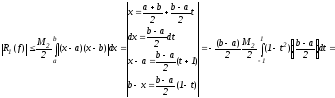
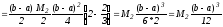 (11)
(11)
Формулы Ньютона-Котеса.
Для
повышения точности формулы трапеций
введем на
 более густую равномерную сетку с шагомh:
более густую равномерную сетку с шагомh:
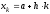 ,
,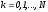 ,
,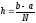 .
.
Используя полученное разбиение, запишем
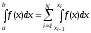
и
применим на каждом отрезке
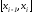 формулу трапеций (10)
формулу трапеций (10)
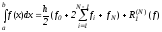 , (12)
, (12)
где
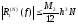 ,
согласно (11).
,
согласно (11).
Формула (12) носит название обобщенной формулы трапеций.
Определение.
Квадратурные формулы с равноотстоящими узлами носят название формул Ньютона-Котеса порядка n с (N+1) узлами, где n- порядок интерполяции.
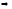 (12)
– формула Ньютона-Котеса порядка n=1
c (N+1)
узлами.
(12)
– формула Ньютона-Котеса порядка n=1
c (N+1)
узлами.
Определение.
Говорят,
что данная квадратурная формула имеет
алгебраическую точность
 ,
если
,
если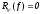 для многочлена степени меньшей или
равной
для многочлена степени меньшей или
равной
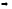 формула
трапеций (10)-точна для многочлена
формула
трапеций (10)-точна для многочлена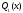 ,то есть, имеет
алгебраическую точность 1.
,то есть, имеет
алгебраическую точность 1.
Теорема 1.
Пусть
n-
четное и соответствующая квадратурная
формула имеет алгебраическую точность
 .Тогда, если узлы
интерполяции расположены симметрично
относительно середины отрезка, причем
точка
.Тогда, если узлы
интерполяции расположены симметрично
относительно середины отрезка, причем
точка
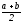 является одним из узлов, то:
является одним из узлов, то:
алгебраическая точность квадратурной формулы повышается на 1, т.е. при n=2m получаем v=2m+1;
коэффициенты квадратурной формулы
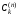 удовлетворяют дополнительным условиям
симметрии
удовлетворяют дополнительным условиям
симметрии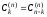 ,
,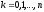 .
.
 Пусть
n=2m
и (2m+1)
узлов x0,
x1,
…, x2m
удовлетворяют условиям симметрии:
Пусть
n=2m
и (2m+1)
узлов x0,
x1,
…, x2m
удовлетворяют условиям симметрии:
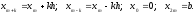
Необходимо
доказать, что квадратурная формула
2m-го
порядка с таким расположением узлов
имеет алгебраическую точность
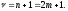 Имеют место следующие очевидные
утверждения:
Имеют место следующие очевидные
утверждения:
Если квадратурная формула точна для какого-либо конкретного полинома степени n+1, то она точна и для любого полинома той же степени (учесть, что по условию квадратурная формула точна для полинома степени n).
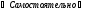
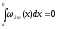 .
.
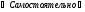
Встроим
в систему узлов ещё один узел
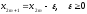 и запишем интерполяционный полином
и запишем интерполяционный полином в форме Ньютона с разделенными разностями:
в форме Ньютона с разделенными разностями:
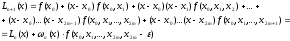
Согласно
свойствам разделенных разностей,
величина
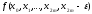 -конечна
при любом
-конечна
при любом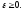
А согласно утверждению 2):
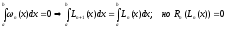 по
условию, следовательно,
по
условию, следовательно,
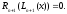
Утверждение
теоремы о симметрии коэффициентов
(весов) квадратурной формулы следует
из симметрии фундаментальных полиномов
(5) относительно центрального узла.

Рассмотрим более подробно случай n=2 (параболическая интерполяция).
Учитывая теорему 1, выберем узлы:

обозначим
 замена
замена

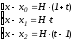
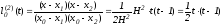 ,
,
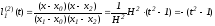 ,
,
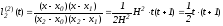 .
.
Вычисляем квадратурные коэффициенты (веса):
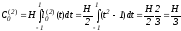 ,
,
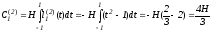 ,
,
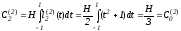 -можно
было не вычислять.
-можно
было не вычислять.
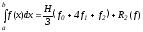 (13)
(13)
-формула
парабол формула
Симпсона.
формула
Симпсона.
Оценим
остаточный член формулы Симпсона.
Согласно (9)
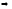
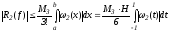 ,
,
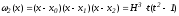 ,
,
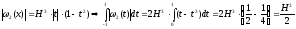 ,
,
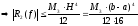 .
(14)
.
(14)
Учитывая теорему 1 о том, что формула Симпсона (13) должна быть точна для многочлена 3-й степени, формулу остаточного члена можно уточнить:
Пусть,
например,
 разложим в ряд Тейлора с остаточным
членом в форме Лагранжа (с центром в
точке
разложим в ряд Тейлора с остаточным
членом в форме Лагранжа (с центром в
точке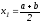 )
)
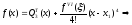
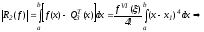
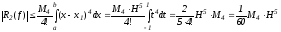
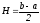 (15)
(15)
Замечание.
Более точная оценка остаточного члена формулы Симпсона (с учетом теоремы 1) приводит к оценке:
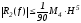 . (15')
. (15')
Для уменьшения погрешности поступим аналогично предыдущему при выводе формулы трапеций. Заметим, что в соответствии с условиями теоремы 1, мы имеем нечетное число узлов, причем последний узел совпадает с b и имеет обязательно четный номер:
Пусть
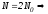 число
узлов=
число
узлов=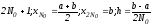
Рассмотрим
отрезок
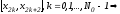
для
тройки узлов
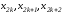 применим формулу парабол:
применим формулу парабол:
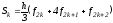 .
.
Просуммируем
по k
(число отрезков
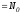 ):
):
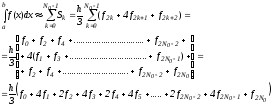 (16)
(16)
Оценим
остаточный член формулы Симпсона (16).
Учитывая (15’), заменяя Н
на
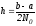 и складывая погрешности на каждом
интервале, получим:
и складывая погрешности на каждом
интервале, получим:
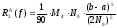 .
.
Лекция 8
