1.3. Задача приближения функций. Интерполяция.

В численном анализе рассматриваются следующие задачи приближения функций:

Задача наилучшего приближения в нормированном пространстве.

Задана функция y(x), некоторый класс функций X и некоторая норма, или метрика.

Найти функцию 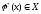, такую что.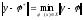

Чаще всего используются нормы 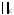и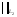, такие что

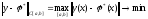, (равномерное приближение)

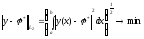. (среднеквадратичное приближение)

Задача приближения полиномами.

Пусть класс X состоит из функций вида

,

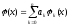где 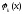- заданная последовательность функций.

Например, при 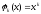получаем задачу приближения алгебраическими полиномами. Пр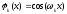иили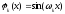- тригонометрическими полиномами и т.п.

Тригонометрическими функциями приближаем, когда строим ряды Фурье.

Общая задача интерполяции.

Пусть f(x) – определена на [a,b] и принадлежит некоторому классу.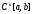

Задана сетка узлов a  x₀ < x₁ <…< x_n  b.

Требуется построить функцию

,

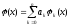линейную относительно функций  _k(x) и такую, что выполняется условие

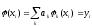, (1)

причем, система {_k(x)}_{k=0, …, n} линейно независима.

Выбор системы {_k(x)} определяется классом функций f(x).

Частный случай – интерполяция многочленами:

{_k(x)} = {x^k}, k = 0, 1, …, n

Пусть L_n(x) – искомый интерполяционный многочлен n-ой степени.

Должно выполняться условие:

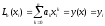. (2)

Определитель системы (2) называется определителем Вандермонда.

.

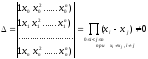Замечание 1.

Система (2) плохо обусловлена, в связи с чем, ее численное решение затруднительно. Понятие плохой обусловленности будет подробно рассмотрено в лекции 11.

Поэтому интерполяционный полином находят другим способом.

Найдем частные полиномы 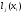, обладающие свойством

.

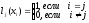В качестве таких полиномов можно взять

.

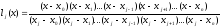Тогда полином 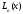, обладающий свойством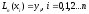, можно записать в виде

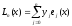. (3)

Очевидно, 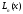- полиномn-го порядка, или n-ой степени. Полученный таким способом полином называют интерполяционным полиномом Лагранжа.

Подведем некоторые итоги.

Итак, поставленная задача интерполяции функции y(x) на сетке узлов 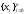алгебраическим полиномомn-ой степени решается с помощью интерполяционного полинома Лагранжа (3).

Теорема 1.

Полином 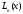- единственное решение задачи (2).

Пусть существует другой полином 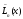такой, что.

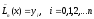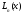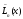Поскольку иполиномы степениn, то 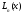--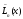 полином степени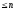, причем в узлах интерполяции разность

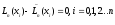
Но полином степени 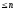не может иметь(n+1) корней, следовательно,

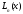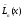=- единственный полином Лагранжа.

Существуют и другие формы представления 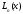помимо (3).

Рассмотрим погрешность аппроксимации функции y(x) с помощью полинома .

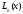Теорема 2.

Пусть функция 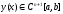,,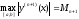 (максимум существует, т.к.(n+1)–я производная непрерывна, следовательно, максимум достигается на отрезке [a,b]). Пусть задана сетка узлов 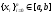,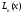- интерполяционный полином Лагранжа. Тогда для погрешности интерполяции справедливы оценки:

, (4)

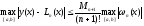, (5)

где 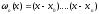- специальный полином (n+1)-ой степени. (6)

Запишем y(x) в виде:

, (*)

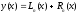где 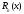- погрешность интерполяции в точкеx[a,b].

Очевидно, что

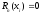, i=0, 1,…, n (7)

С учетом (7) 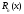можно искать в виде

.

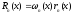Зафиксируем ,

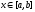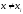
Рассмотрим функцию

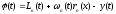. (8)

Очевидно, 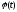обращается в 0 в(n+2) -х точках

t=x:

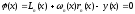(см. (*))

:

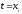, (см. (6)) i=0,1,2…n

По теореме Ролля на интервале (a,b) существует, по крайней мере, (n+1) точка, в которой 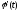обращается в 0.

По теореме Ролля на интервале (a,b) существует, по крайней мере, n точек, которых .

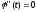И так далее…

Существует, по крайней мере, одна точка 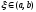такая, что.

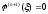Учитывая, что

,

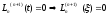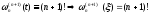
и дифференцируя (n+1) раз формулу (8) по t в точке 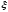получим

,

.

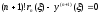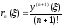Поэтому

.

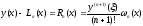Отсюда следуют (4) и (5).

Пример 1.

Пусть 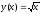, [a,b] - отрезок [100,144].

Построить интерполяционный многочлен второго порядка L₂(x) в узлах

, ,.

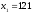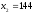Оценить погрешность интерполяции в т. x=116 и на всем отрезке [a,b].

,

,

,

.

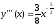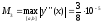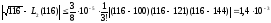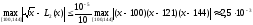Лекция 3.