4.2.1. Оценка погрешности метода Эйлера.

Будем считать, что ошибка округления имеет порядок не меньший, чем 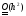. Тогда из (9) следует:

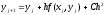(10)

Разложим точное решение 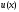задачи (5) в точке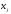с такой же точностью:

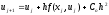(11)

Вычтем(11) из (10) 

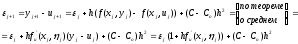(12)

где

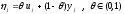
В силу условий теоремы существования и единственности частные производные 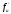ограничены в прямоугольнике:

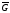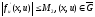
Обозначим 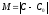и оценим (12) по модулю

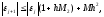(13)

по условию.

Обозначим

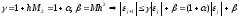(14)

Теорема 2.

Для метода Эйлера имеет место следующая оценка погрешности:

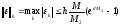(15)

Из (13) следует (рекурсия назад)

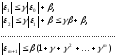
Используя алгебраическое тождество

получаем

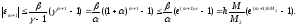(16)

(В последнем неравенстве использовано свойство второго замечательного предела)

Учитывая, что

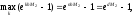
получим

,

т.е. оценку (15).

Замечание.

Из соотношения (16) следует, что

1. 1. Ошибка растет с номером шага k.

2. 2. Порядок ошибки в методе Эйлера .

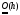4.2.2.Методы Рунге-Кутта.

Методы Рунге-Кутта - это группа итерационных методов решения задачи Коши (4), характеризуемая следующими условиями:

1. Это одношаговые методы, т.е. при переходе из точки 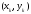в точку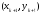используется лишь информация о предыдущей точке. Этому условию соответствует такая общая запись итерационной процедуры

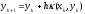, (17)

где 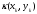выражается через значения функции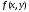в точкеили близким к ней (сдвинутым на долю шага).

2. Процедура (16) согласуется с рядом Тейлора вплоть до членов порядка , гдеp -порядок метода.

3. Метод не использует производных от 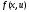, а требует только вычисления функции в различных точках сетки, причем число вычислений функции - минимально возможное для данного порядка.

Заметим, что метод Эйлера является частным случаем метода Рунге-Кутта, имеющий наименьший первый порядок точности. Рассмотрим один из примеров повышения порядка точности метода Рунге-Кутта (16) до второго порядка.

Представим 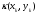в виде следующей линейной комбинации

.

Разложим функцию 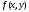в точкев ряд Тейлора до членов первого порядка включительно

.

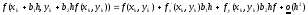Подставляя эти формулы в (16) , получим:

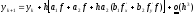. (18)

(все входящие в правую часть функции берутся в точке )

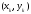Аналогичное разложение по Тейлору напишем для функции 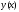, используя уравнение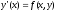

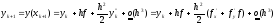. (19)

Требуя совпадения коэффициентов разложений (18) и (19) при одинаковых степенях h, получим систему уравнений для неизвестных коэффициентов :

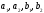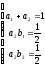(20)

Система (20) недоопределена. Поэтому один из коэффициентов можно задать произвольно.

Например, положим .

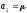Решая (20), получим

.

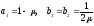Итерационная процедура (17) приобретает вид

. (21)

Учитывая результат теоремы 2, заключаем, что точность этого метода 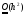, т.е. данный метод - второго порядка.

Рассмотрим некоторые частные случаи процедуры (21).

Отбрасывая погрешность, получаем

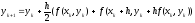. (22)

Полученный метод Рунге-Кутта носит название “предиктор-корректор”. Чтобы прояснить смысл этого названия разобьем процедуру (22) на два этапа:

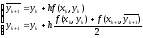
На первом этапе “предсказываем” значение 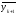по методу Эйлера. На втором этапе это значение корректируется путем усреднения угловых коэффициентов в точках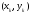и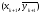. За счет коррекции, точность данного метода и повышается на порядок по сравнению с методом Эйлера.

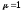
Согласно (21) , получаем

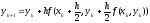. (23)

Обозначим

.

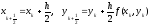Тогда (23) разбивается на два этапа:

На первом этапе находим 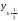- прогнозируемое значение на половинном шаге от точки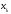по методу Эйлера.

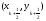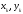Вычисляем наклон интегральной кривой в точке , и на втором этапе, двигаясь по касательной с данным угловым коэффициентом из точки () в точку (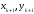), получаем окончательноПолученный метод носит название “модифицированный метод Эйлера”.

Замечание 1.

Существуют процедуры Рунге-Кутта повышенной точности (порядка 3, 4, 5…). Например, метод Рунге-Кутта четвертого порядка точности (наиболее употребляемый на практике) сформулирован следующим образом

где

(24)

Если 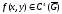, то погрешность процедуры.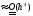

Замечание 2.

При практическом применении методов Рунге-Кутта возникает вопрос: какой формулой пользоваться на практике? Если априори известно, что 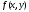- достаточно гладкая функция, например,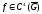, то наиболее эффективна процедура (24). Если же гладкость функциинедостаточна, то лучше использовать методы второго и третьего порядка.

Замечание 3.

В среде МАТЛАБ реализованы две процедуры Рунге-Кутта:

ode23 – метод второго и третьего порядка

и ode45 - метод четвертого и пятого порядка.

В лабораторной работе 7 предусмотрено знакомство с этими командами.

Лекция 13.