5709 Mmmmmdссiiiiiiiii,
5709 = МММММDCCIX (= 51000+500+ +2100 +(10–1)).
Разница между этими системами записи чисел заключается в том, что в первой значение каждой цифры изменяется в зависимости от её позиции – она может обозначать количество единиц, количество десятков, сотен, тысяч, и.т.д., – а во второй цифра сохраняет своё значение независимо от позиции. Системы записи первого типа называются позиционными системами счисления, а системы второго типа – непозиционными.
Как будет доказано
ниже, каждое натуральное число можно
однозначно разложить не только по
степеням числа 10,
но и по степеням любого наперёд заданного
натурального числа q
> 1. Этим
оправдано следующее определение:
говорят, что натуральное число k
записано в
виде систематического
числа (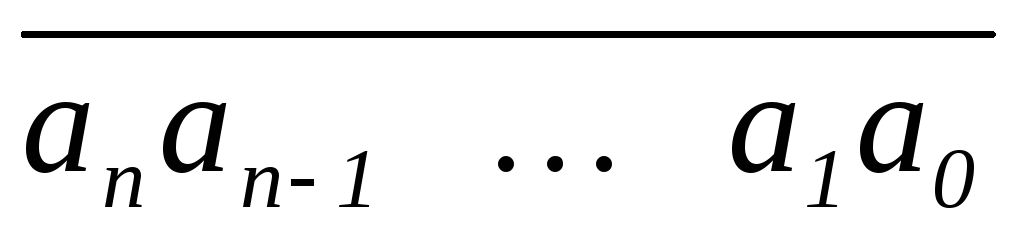
)q
в позиционной
q-чной
системе счисления (скобки
и черта в конкретных случаях не ставятся),
если
k = anqn + an–1qn–1 + … + a1q + a0 ,
где числа ai удовлетворяют условиям 0 ai < q (0 i n – 1), an > 0 и называются цифрами числа n в рассматриваемой q-чной системе счисления. Если q > 10, то для обозначения цифр, больших 9, используют круглые скобки или последовательные начальные буквы латинского алфавита: например, (10) или A обозначает цифру 10, (11) или B – цифру 11, (12) или С – цифру 12, а (17) или H – обозначает цифру 17.
Примеры: 1. 12310 = 1738 = 7B16 = 11110112 , т.к.
12310 = 1102 + 210 + 3 = 182 + 78 + 3 =
= 716 + 11 = 126 + 125 + 124 + 123 + 022 + 12 + 1.
2. 570910 = 131158 = 164(13)16 = 164D16 = 10110010011012 = 105709 .
Теорема (о q-чных
позиционных системах счисления).
Любое натуральное число обладает
единственным представлением в виде
систематического числа
в позиционной
системе счисления с произвольным
натуральным основанием q > 1.
Доказательство. Необходимо доказать, что для любого натурального числа k найдутся однозначно определённые цифры a0 , … , an (0 ai < q , 0 i n – 1, an > 0) со свойством k = anqn + an–1qn–1 + … + a1q + a0 .
Ясно, что k = (anqn–1 + an–1qn–2 + … + a1)q + a0 и 0 a0 < q, т.е. a0 – остаток от деления числа k на q, а anqn–1 + an–1qn–2 + … + a1 = k0 – частное, которые определены однозначно.
Аналогично имеем: k0 = (anqn–2 + an–1qn–3 + … + a2)q + a1 = k1q+a1 и q-чная цифра a1 – это остаток от деления числа k0 на q. Продолжая этот процесс, находим:
При этом обязательно найдётся такое n N0 , что kn–1 < q: действительно, если ki q , то, по построению, k > k0 > k1 > … – бесконечная убывающая цепочка натуральных чисел, что невозможно. Итак, эти формулы однозначно определяют q-чные цифры a0 , … , an числа k.
Теорема доказана.
Позиционные системы счисления с основаниями, не равными 10, широко используются в различных областях человеческой деятельности. В частности, в информатике для представления чисел в ЭВМ применяется двоичная система счисления, а для визуализации двоичных чисел часто применяются более экономные 8-ричная и 16-ричная системы счисления.
Обилие систем счисления с различными основаниями требует умения переводить числа из одной системы счисления в другую.