Глава II. Некоторые диофантовы уравнения

Диофантово уравнение – это уравнение вида P(x₁ , … , x_n) = 0, где левая часть представляет собой многочлен от переменных x₁ , … , x_n с целыми коэффициентами. Любой упорядоченный набор (u₁ ; … ; u_n) целых чисел со свойством P(u₁ , … , u_n) = 0 называется (частным) решением диофантова уравнения P(x₁ , … , x_n) = 0. Решить диофантово уравнение – значит найти все его решения, т.е. общее решение этого уравнения.

Примеры: 1. Диофантово уравнение 5x – 1 = 0 не имеет решений.

2. Диофантово уравнение 5x – 10 = 0 имеет решение x = 2, которое является единственным.

3. Уравнение ln x – 8x² = 0 не является диофантовым.

4. Часто уравнения вида P(x₁ , … , x_n) = Q(x₁ , … , x_n), где P(x₁ , … , x_n), Q(x₁ , … , x_n) – многочлены с целыми коэффициентами, также называют диофантовыми. Их можно записать в виде P(x₁ , … , x_n) – Q(x₁ , … , x_n) = 0, который является стандартным для диофантовых уравнений.

5. x² – y² = a – диофантово уравнение второй степени с двумя неизвестными x и y при любом целом a. Оно имеет решения при a = 1, но не имеет решений при a = 2.

§ 1. Линейные диофантовы уравнения

Пусть a₁ , … , a_n , с  Z . Уравнение вида a₁x₁ + … + a_nx_n = c называется линейным диофантовым уравнением с коэффициентами a₁ , … , a_n , правой частью c и неизвестными x₁ , … , x_n . Если правая часть с линейного диофантова уравнения нулевая, то такое диофантово уравнение называется однородным.

Наша ближайшая цель – научиться находить частные и общие решения линейных диофантовых уравнений с двумя неизвестными. Очевидно, что любое однородное диофантово уравнение a₁x₁ + … + a_nx_n = 0 всегда имеет частное решение (0; … ; 0).

Очевидно, что линейное диофантово уравнение, все коэффициенты которого равны нулю, имеет решение только в случае, когда его правая часть равна нулю. В общем случае имеет место следующая

Теорема (о существовании решения линейного диофантова уравнения). Линейное диофантово уравнение a₁x₁ + … + a_nx_n = c , не все коэффициенты которого равны нулю, имеет решение тогда и только тогда, когда НОД(a₁ , … , a_n) | c.

Доказательство. Необходимость условия очевидна: НОД(a₁ , … , a_n) | a_i (1  i  n), так что НОД(a₁ , … , a_n) | (a₁x₁ + … + a_nx_n), а значит, делит и c = a₁x₁ + … + a_nx_n .

Пусть D = НОД(a₁ , … , a_n), с = Dt и a₁u₁ + … + a_nu_n = D – линейное разложение наибольшего общего делителя чисел a₁ , … , a_n . Умножая обе части на t, получим a₁(u₁t) + … + a_n(u_nt) = Dt = c, т.е. целочисленная n-ка (x₁t; … ; x_nt) является решением исходного уравнения с n неизвестными.

Теорема доказана.

Эта теорема даёт конструктивный алгоритм для нахождения частных решений линейных диофантовых уравнений.

Примеры: 1. Линейное диофантово уравнение 12x+21y = 5 не имеет решений, поскольку НОД(12, 21) = 3 не делит 5.

2. Найти частное решение диофантова уравнения 12x+21y = 6.

Очевидно, что теперь НОД(12, 21) = 3 | 6, так что решение существует. Запишем линейное разложение НОД(12, 21) = 3 = 122 + 21(–1). Поэтому пара (2; –1) – частное решение уравнения 12x+21y = 3, а пара (4; –2) – частное решение исходного уравнения 12x+21y = 6.

3. Найти частное решение линейного уравнения 12x + 21y – 2z = 5.

Так как (12, 21, –2) = ((12, 21), –2) = (3, –2) = 1 | 5, то решение существует. Следуя доказательству теоремы, вначале найдём решение уравнения (12, 21)х – 2у = 5, а затем, подставив линейное разложение наибольшего общего делителя из предыдущей задачи, получим решение исходного уравнения.

Для решения уравнения 3х – 2у = 5 запишем линейное разложение НОД(3, –2) = 1 = 31 – 21 очевидно. Поэтому пара чисел (1; 1) является решением уравнения 3x – 2y = 1, а пара (5; 5) – частным решением диофантова уравнения 3х – 2у = 5.

Итак, (12, 21)5 – 25 = 5. Подставляя сюда найденное ранее линейное разложение (12, 21) = 3 = 122 + 21(–1), получим (122+21(–1))5 – 25 = 5, или 1210 + 21(–5) – 25 = 5, т.е. тройка целых чисел (10; –5; 5) является частным решением исходного диофантова уравнения 12x + 21y – 2z = 5.

Теорема (о структуре общего решения линейного диофантова уравнения). Для линейного диофантова уравнения a₁x₁ + … + a_nx_n = c справедливы следующие утверждения:

(1) если = (u₁ ; … ; u_n), = (v₁ ; … ; v_n) – его частные решения, то разность = = (u₁ – v₁ ; … ; u_n – v_n) – частное решение соответствующего однородного уравнения a₁x₁ + … + a_nx_n = 0,

(2) множество частных решений линейного диофантова однородного уравнения a₁x₁ + … + a_nx_n = 0 замкнуто относительно сложения, вычитания и умножения на целые числа,

(3) если M – общее решение данного линейного диофантова уравнения, а L – общее решение соответствующего ему однородного диофантова уравнения, то для любого частного решения = (u₁ ; … ; u_n) исходного уравнения верно равенство M = + L .

Доказательство. Вычитая равенство a₁v₁ + … + a_nv_n = c из равенства a₁u₁ + … + a_nu_n = c, получим a₁(u₁ – v₁) + … + a_n(u_n – v_n) = 0, т.е. набор (u₁ – v₁ ; … ; u_n – v_n) – частное решение линейного однородного диофантова уравнения a₁x₁ + … + a_nx_n = 0. Таким образом, доказано, что

 = (u₁ ; … ; u_n), = (v₁ ; … ; v_n)  M  L .

Это доказывает утверждение (1).

Аналогично доказывается утверждение (2):

 ,  L  z  Z  L  z L .

Для доказательства (3) вначале заметим, что M  + L. Это следует из предыдущего:   M  +L .

Обратно, если = (l₁ ; … ; l_n)  L и = (u₁ ; … ; u_n)  M, то  M:

a₁(u₁ + l₁)+ …+a_n(u_n + l_n) = (a₁u₁ + … + a_nu_n)+(a₁l₁ + … + a_nl_n) = c + 0 = c.

Таким образом, + L M, и в итоге M = + L.

Теорема доказана.

Доказанная теорема имеет наглядный геометрический смысл. Если рассмотреть линейное уравнение a₁x₁ + … + a_nx_n = c, где х_i  R, то как известно из геометрии, оно определяет в пространстве Rⁿ гиперплоскость, полученную из плоскости L c однородным уравнением a₁x₁+ … +a_nx_n=0, проходящей через начало координат, сдвигом на некоторый вектор  Rⁿ. Поверхность вида + L называют также линейным многообразием с направляющим пространством L и вектором сдвига . Таким образом, доказано, что общее решение М диофантова уравнения a₁x₁ + … + a_nx_n = c состоит из всех точек некоторого линейного многообразия, имеющих целые координаты. При этом координаты вектора сдвига тоже целые, а множество L решений однородного диофантова уравнения a₁x₁ + … + a_nx_n = 0 состоит из всех точек направляющего пространства с целыми координатами. По этой причине часто говорят, что множество решений произвольного диофантова уравнения образует линейное многообразие с вектором сдвига и направляющим пространством L.

Пример: для диофантова уравнения х – у = 1 общее решение M имеет вид (1+у; у), где у  Z, его частное решение = (1; 0), а общее решение L однородного уравнения х – у = 0 запишется в виде (у; у), где у  Z . Таким образом, можно нарисовать следующую картинку, на которой решения исходного диофантова уравнения и соответствующего однородного диофантова уравнения изображены жирными точками в линейном многообразии М и пространстве L соответственно.

Исследуем теперь, как выглядит общее решение однородного диофантова уравнения с двумя неизвестными.

Теорема (об общем решении диофантова уравнения ax + by =0). Если D = НОД(a, b), и a = Da₁ , b = Db₁ , то общее решение линейного однородного диофантова уравнения ax + by = 0 имеет вид

L = {(b₁t ; –a₁t)  ZZ | t  Z}.

Доказательство. Очевидно, что любая пара чисел х = b₁t , у = –a₁t (t  Z) удовлетворяет уравнению ax + by = 0  a₁x + b₁y = 0.

Обратно, ввиду ax + by = 0  a₁x + b₁y = 0 и взаимной простоты чисел а₁ , b₁ , из b₁ | a₁x получаем х = b₁t для некоторого t  Z. Подставив х в равенство a₁x = b₁(–y), найдём y = –a₁t, что и требовалось.

Теорема доказана.

Без доказательства сформулируем следующий общий результат, который можно вывести из доказанной теоремы, проведя индукцию по числу неизвестных n.

Теорема (об общем решении линейного диофантова уравнения с n неизвестными а₁х₁ + … + а_nх_n = 0). Для линейного однородного диофантова уравнения a₁x₁ + … + a_nx_n = 0 существует такая целочисленная матрица P  M(n–1, n, Z), что P, а общее решение этого уравнения зависит от n–1 целочисленного параметра t₁ , … , t_n–1 и имеет вид

M = { P | = (t₁ ; … ; t_n-1)  Z^n–1 }.

Очевидно, что в случае n = 2 матрица Р – это просто строка (b₁ ; –a₁).

Примеры: 1. Решить диофантово уравнение 12x + 21y = 6.

В предыдущих примерах было найдено частное решение (4; –2) этого диофантова уравнения. Согласно доказанной теореме, общее решение однородного уравнения 12x + 21y = 0 имеет вид (7t; –4t), t  Z или (нужно учесть, что НОД(12; 21) = 3 и 12x+21y = 0   4x = 7(–y)). Поэтому общее решение рассматриваемого диофантова уравнения имеет вид (4 + 7t;–2 – 4t), t  Z или .

2. Найти общее решение диофантова уравнения 12x + 21y – 2z = 5.

Частное решение (10; –5; 5) этого уравнения было найдено ранее, найдём общее решение однородного уравнения 12x + 21y – 2z = 0, эквивалентного диофантову уравнению 12x + 21y = 2z.

Для разрешимости этого уравнения необходимо и достаточно выполнение условия НОД(12, 21) = 3 | 2z, т.е. 3 | z или z = 3t для некоторого целого t. Сокращая обе части на 3, получим 4x + 7y = 2t. Частное решение (2; –1) диофантова уравнения 4x + 7y = 1 найдено в предыдущем примере. Поэтому (4t ; –2t) – частное решение уравнения 4x + 7y = 2t при любом t  Z. Общее решение соответствующего однородного уравнения (7u ; –4u) уже найдено. Таким образом, общее решение уравнения 4x + 7y = 2t имеет вид: (4t + 7u ; –2t – 4u), а общее решение однородного уравнения 12x + 21y – 2z = 0 запишется так: (4t + 7u ; –2t – 4u ; 3t).

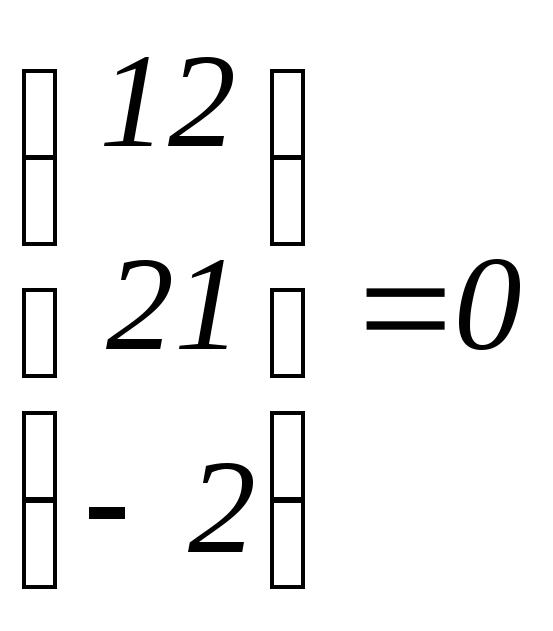Нетрудно убедиться, что этот результат соответствует сформулированной выше без доказательства теореме о решениях однородного диофантова уравнения а₁х₁ + … + а_nх_n = 0: если Р = , тоР и (u; t)P – общее решение рассматриваемого однородного уравнения.

Итак, общее решение диофантова уравнения 12x + 21y – 2z = 5 выглядит так: (10 + 4t + 7u ; –5 – 2t – 4u ; 5 + 3t).

3. На примере предыдущего уравнения проиллюстрируем другой метод решения диофантовых уравнений от многих неизвестных, который состоит в последовательном уменьшении максимального значения модулей его коэффициентов.

12x + 21y – 2z = 5  12x + (102 + 1)y – 2z = 5 

 12x + y – 2(z – 10y) = 5 

 .

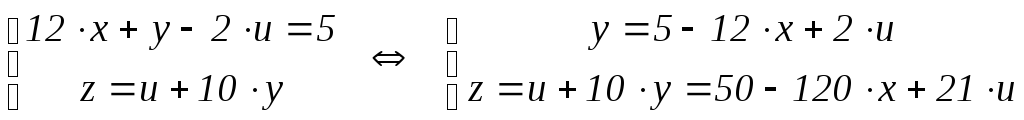Таким образом, общее решение рассматриваемого уравнения можно записать и так: (x; 5 – 12x + 2u ; 50 – 120x + 21u), где x, u – произвольные целые параметры.

Упражнение: Докажите, что множества решений, найденные разными способами, совпадают, т.е.

{(10 + 4t + 7u ; –5 – 2t – 4u ; 5 + 3t)  Z³ | u, t  Z} =

= {(x; 5 – 12x + 2u ; 50 – 120x + 21u)  Z³ | x, u  Z}

4. Ещё пример: решить диофантово уравнение 5x – 9y + 14z = 8.

5x – 9y + 14z = 8  5x – 9y +(52 + 4)z = 8 

 5(x + 2z) – 9y + 4z = 8 

 

 .

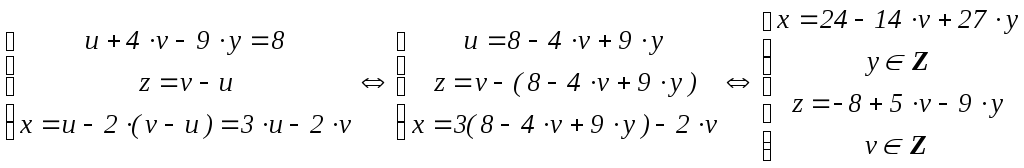Таким образом, общее решение рассматриваемого уравнения выглядит так: (24 – 14 v + 27y, y, –8 + 5v – 9y), где y, v – произвольные целочисленные параметры.

Упражнения: 1. Найдите всеми возможными способами общие решения следующих диофантовых уравнений: 32x + 52y = 22, 13x + 15y – 23z = 1, 2x + 4y –6z – 8t = 12.

2. Найдите все целые числа x, y, удовлетворяющие диофантову уравнению 23x – 34y = 5, для которых величина |x| + |y| а) минимальна, б) не превосходит 100 и максимально возможна.

3. Два весёлых портных ставят метки на ленте длиной 100 м. Первый портной ставит свои метки через каждые 17 см., а второй – через каждые 25 см. На каких расстояниях от начала ленты будет стоять метка первого портного, на расстоянии не более 2 см. от которой второй портной также поставит свою метку ? Укажите последнюю метку первого портного с этим свойством.

4. Докажите, что монетами 3 дублона и 5 дублонов можно сдать любую сдачу, большую 7 дублонов (количество монет не ограничено).