§ 11. Признаки делимости

Признак делимости на число m  N – это такая процедура (алгоритм), которая сводит задачу о делимости данного большого числа на m к аналогичной равносильной задаче для гораздо меньшего числа. Например, признак делимости на 2 утверждает, что число делится на 2 тогда и только тогда, когда делится на 2 последняя (младшая) цифра этого числа. Таким образом, вместо самого многозначного числа признак делимости на 2 рекомендует делить на 2 только одну цифру.

Из школьного курса известны признаки делимости на 2, 4, 5, 25, 3, 9. Оказывается, что все они укладываются в одну схему.

Пусть даны натуральные число m , и число k = , записанное в десятичной системе счисления, b₀ , … , b_n – фиксированные целые числа, причём b_i  10ⁱ (mod m) (0  i  n). Целое число m(k) = a_nb_n + … + a₁b₁ + a₀b₀ (mod m) назовём т-индикатором числа k .

Примеры: 1. Пусть m = 3, b_i = 1 (0  i  n). Тогда имеем 10ⁱ  1ⁱ = b_i (mod 3). Поэтому выражение 3(k) = a_n + …+ a₀ является 3-индикатором числа k = .

2. В предыдущем примере можно было бы взять и другие числа b_i , например, b_i = 4 (0  i  n) также годятся, т.к. 4  1 (mod 3). Поэтому выражение 3(k) = 4a_n + …+ 4a₀ тоже является 3-индикатором числа k = .

3. Проверьте самостоятельно, что 9(k) = a_n + …+ a₀ является 9-индика­тором числа k = .

Приведённые примеры показывают, что т-индикаторы определены не однозначно – они зависят от конкретного выбора чисел b_i (0  i  n), в качестве которых всегда можно взять, например, остатки от деления чисел 10ⁱ на т.

Теорема (обобщённый признак делимости Паскаля). Пусть заданы произвольное натуральное число m и число k = в десятичной системе счисления. Тогдаk  m(k) (mod m). В частности, k  m тогда и только тогда, когда m(k)  m.

Доказательство. Ввиду 10ⁱ  b_i (mod m) имеем

k = = a_n10ⁿ + a_n–110^n–1 + … + a₁10 + a₀ 

 a_nb_n + a_n–1b_n–1 + … + a₁b₁ + a₀b₀ = m(k) (mod m).

В частности, k  m  k  0 (mod m)  m(k)  0 (mod m)  m(k)  m.

Теорема доказана.

Следствие 1 (известные признаки делимости). Для числа k = справедливы следующие утверждения:

(1) для любого s (1 s n) верно k 2^s   2^s ,

(2) для любого s (1 s n) верно k 5^s   5^s ,

(3) k  3  (a_n + … + a₀)  3,

(4) k  9  (a_n + … + a₀)  9,

(5) k  11  (a_n(–1)ⁿ + … + a_i(–1)ⁱ + … + a₀)  11.

Доказательство. (1), (2) Обозначая через m числа 2^s или 5^s (в зависимости от доказываемого утверждения), имеем 10ⁱ  10ⁱ (mod m ) при i < s и 10ⁱ  0 (mod m) при i  s. Поэтому, если в обобщённом признаке делимости Паскаля положить b_i = 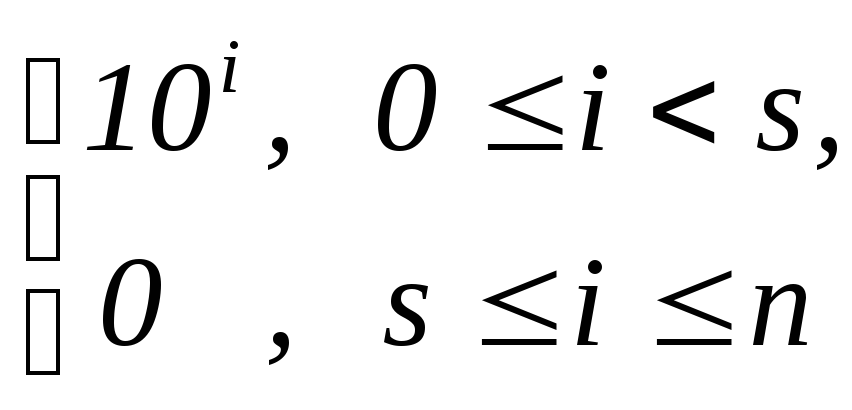, то

k  т  (a_n0 + … + a_s0 + a_s–110^s–1 + … + a₀10⁰)  т   т.

(3), (4) Снова, обозначая через m числа 3 или 9 (в зависимости от доказываемого утверждения), получим 10ⁱ  1 (mod m), так что всё следует из признака делимости Паскаля.

(5) Легко видеть, что 10ⁱ  (–1)ⁱ (mod 11), т.е. в качестве b_i в признаке делимости Паскаля можно взять (–1)ⁱ.

Следствие 1 доказано.

Следствие 2 (признак делимости на 7). Для числа k = выполнены следующие утверждения:

(1) трёхзначное число k = делится на 7 тогда и только тогда, когда7(k) = a₀ + 3a₁ + 2a₂ делится на 7,

(2) если число k разбито справа налево на грани g_i = по три десятичных цифры в каждой (0 i  + 1), то k 7 в том и только том случае, когда (g₀ – g₁ + … + (–1)ⁱg_i + …)  7,

(3) в условиях утверждения (2) k  7 в том и только том случае, когда (7(g₀) – 7(g₁) + … + (–1)ⁱ7(g_i) + …)  7.

Доказательство. (1) следует непосредственно из признака делимости Паскаля при b₀ = 1  10⁰, b₁ = 3  10¹, b₂ = 2  10² (mod 7).

(2) Ясно, что выполнено равенство k = g₀ + g₁10³ + g₂10⁶ + … , причём, 10³ = 7143 – 1  –1 (mod 7). Поэтому 10^3i  (–1)ⁱ и, как и при доказатель­стве признака делимости Паскаля,

k = g₀ + g₁10³ + g₂10⁶ + …  g₀ – g₁ + … + (–1)ⁱg_i + … (mod 7).

(3) Положим b_6i = 1, b_6i+1 = 3, b_6i+2 = 2, b_6i+3 = –1, b_6i+4 = –3, b_6i+5 = –2 (i  N₀). Тогда можно убедиться, что 10^s  b_s (mod 7). Значит

7(k) = a₀b₀ + … + a_nb_n =

= (a₀1 + a₁3 + a₂2)–(a₃1 + a₄3 + a₅2)+…+(–1)ⁱ(a_3i1 + a_3i+13 + a_3i+22)+… = = 7(g₀) – 7(g₁) + … + (–1)ⁱ7(g_i) + … .

Следствие 2 доказано.

Примеры: 1. Делится ли на 7 число 89653421567 ?

89.653.421.567 = 089.653.421.567  567 – 421 + 653 – 089 

 (17 + 36 + 25) – (11 + 32 + 24) + (13 + 35+ 26) – (19 + 38 + 20) 

 0 – 1 + 2 – 5 = –4  3 (mod 7).

Таким образом, число даёт остаток 3 при делении на 7, и не делится на 7.

2. Делится ли на 7 число 82936455364728195106114 ?

gi	082	936	455	364	728	195	106	114
7(gi)	–2	–2	0	0	0	–1	1	2
7(k)	–(–2)+(–2)–0+0–0+(–1)–1+2 = 0

Итак, исходное число делится на 7.

Упражнение: Сформулируйте признаки деления на 13, 15, 27.

Замечание. Признаки делимости не всегда удобно формулировать, конструируя m-индикаторы. Хотя, как правило, удачно выбранный m-индикатор и минимизирует вычисления (что особенно важно при программировании на ЭВМ), но расплачиваться приходится трудностью запоминания получающихся признаков делимости, в чём читатель уже имел возможность убедиться, изучив признак делимости на 7. Следующая теорема показывает альтернативный путь – пусть менее короткий для вычислений, но зато более запоминающийся.

Теорема (признаки делимости на 7, 11, 13). Число k = с количеством цифрn  3 делится на 7, 11, 13 тогда и только тогда, когда на эти числа делится разность чисел, записанных его старшими (n – 3)-мя цифрами и младшими 3-мя цифрами соответственно.: если m  {7, 11, 13}, то  m  (–) m .

Доказательство. Всё следует из a1000 + b  –a + b (mod m).

Теорема доказана.

Упражнение: Докажите, что 10a + b  11  b – a  11, 10a + b  19   a + 2b  19.