О распределении простых чисел

Для каждого положительного действительного числа x обозначим через (x) количество простых чисел в интервале (–, x]. Таким образом, получаем отображение  : R N (называемое функцией Чебышева), значение которого можно вычислить для любого конкретного x  R. Например, (x) = 0 при x < 2, (2) = 1 = (2,99), (3) = 2, (10) = 4 = (7,001). Возникает вопрос о поведении функции (x), более точно – о её порядке роста. Ограничимся только формулировками самых ранних и простых (но далеко не очевидных) результатов на эту тему:

Теорема (неравенства Чебышева). (1) Существуют такие константы 0 < a < 1 < b (например, годятся a = 0,92129, b = 1,0555), что для всех достаточно больших значений x  R верны неравенства

.

Эта теорема была доказана в 1850 г. Кроме того, П.Л.Чебышевым было доказано, что если существует 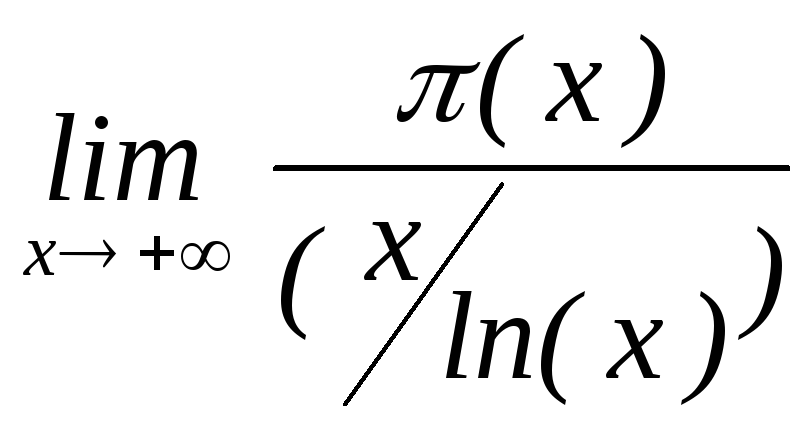, то он равен 1. Существование же этого предела удалось доказать только спустя полвека, используя теорию функций комплексного переменного.

Теорема (Адамар, Валле-Пуссен) Предел 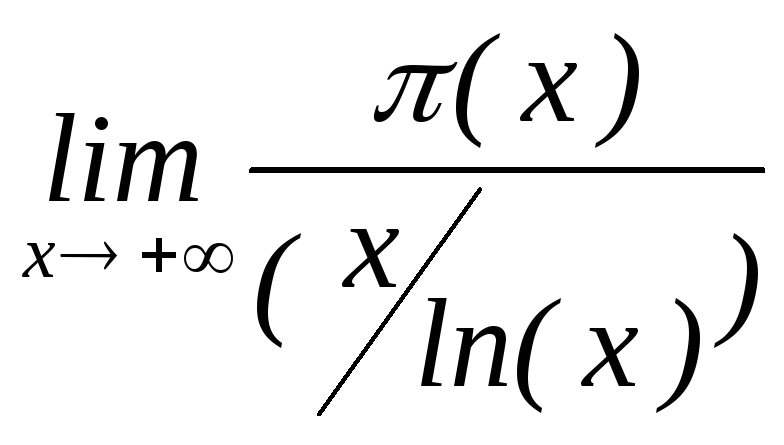существует и равен 1 (асимптотический закон распределения простых чисел).

В той же основополагающей работе П.Л.Чебышева, было дано доказательство следующей известной гипотезы

Теорема (постулат Бертрана). Для любого натурального числа n на отрезке [n; 2n] содержится хотя бы одно простое число.

В то же время, как показывает следующая теорема, существуют сколь угодно длинные отрезки, не содержащие простых чисел.

Теорема (о сколь угодно длинных отрезках, не содержащих простых чисел). Для любого натурального п на отрезке [п! + 2, п! + п] нет ни одного простого числа.

Доказательство. Любое число из рассматриваемого отрезка имеет вид п! + k, где 2  k  n , и делится на k.

Теорема доказана.

Хотя современная теория чисел продвинулась далеко вперёд, многие вопросы о простых числах остаются нерешёнными и по сей день. Например, до сих пор неизвестно – конечны ли множества простых чисел вида 1 + n² и 1 + 2ⁿ (n  Z).

§ 8. Язык сравнений

Пусть a, b, m  Z и m  0. Говорят, что числа a и b сравнимы по модулю m, если разность a – b делится нацело на m: a  b (mod m). Таким образом, a  b (mod m)   t  Z a – b = mt.

Примеры: 1. 5  17 (mod 6), т.к. 5 – 17 = –12 = 6(–2),

3  –5 (mod 4), т.к. 3 – (–5) = 8 = 42,

2. –3 –2 (mod 5), т.к. –3 – (–2) = 1 и 5 1,

28 15 (mod 3), т.к. 28 – 15 = 13 и 3 13.

Свойства сравнений

1⁰. Числа a и b сравнимы по модулю m тогда и только тогда, когда они дают одинаковые остатки при делении на m.

Действительно, если a  b (mod m), а r и s – остатки от деления a и b на m соответственно, то a = mq + r, b = mp + s, 0 r < |m|, 0 s < |m| , причём a – b = m(q – p) + (r – s) делится нацело на m. Это возможно лишь в том случае, когда m | (r – s), т.е. r = s (поскольку –m < r – s < m).

Обратно, если числа a и b дают одинаковые остатки при делении на m, то a = mq + r, b = mp + r, 0 r < m. Поэтому a – b = m(q – p) кратно m , что и требовалось доказать.

Следующие три свойства следуют из 1⁰.

2⁰. Условия a  b и a  0 (mod b) эквивалентны.

В самом деле, a  b  a – 0  b  a  0 (mod b).

3⁰. Любое целое число a сравнимо само с собой по любому модулю m (рефлексивность отношения сравнимости).

4⁰. Если a  b (mod m), то b  a (mod m) (симметричность отношения сравнимости).

5⁰. Если a  b (mod m) и b  с (mod m), то a  c (mod m) (транзитивность отношения сравнимости).

Вместе свойства 2⁰-3⁰ дают

6⁰. Если a  b (mod m), то для любого целого числа c справедливо

a ± c  b ± c (mod m) , ac  bc (mod m).

В самом деле, если a – b = mt, то (a ± c) – (b ± c) = a – b = mt и аналогично ac – bc = (a – b)c = mtc.

7⁰. Если a  b (mod m) и c  d (mod m), то a ± c  b ± d (mod m).

Действительно, если a – b = mt , c – d = ms , то

(a ± c) – (b ± d) = (a – b) ± (c – d) = mt – ms = m(t – s).

8⁰. Если a  b (mod m) и c  d (mod m), то ac  bd (mod m).

В самом деле, если a – b = mt , c – d = ms, то

(ac) – (bd) = aс – bс + bc – bd = (a – b)c + b(c – d) =

= mtc – bms = m (tc – bs).

9⁰. Если a  b (mod m), то для любого натурального k верно сравнение a^k  b^k (mod m).

При k = 1 сравнение верно по условию. Отсюда последовательно получаем, умножая на то же сравнение a  b (mod m):

a²  b² (mod m), a³  b³ (mod m), … , a^k  b^k (mod m).

10⁰. Если целые числа a, b, m делятся нацело на число d  Z \ {0}, то a  b (mod m) тогда и только тогда, когда .

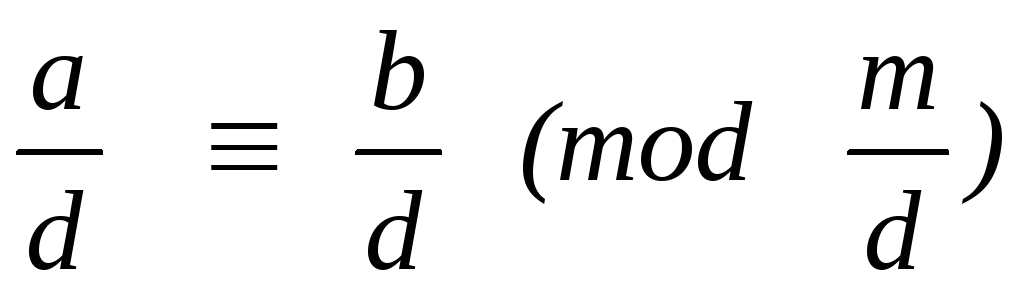Действительно, если a = da₁ , b = db₁ , m = dm₁ , то

a – b = mt  a₁ – b₁ = m₁t .

11⁰. Если da  db (mod m) и НОД(d , m) = 1, то a  b (mod m).

В самом деле, если da – db = mt , то d | mt . Поскольку числа d и m взаимно простые, то по основному свойству взаимно простых чисел d | t , т.е. t = dt₁ для некоторого целого t₁ . Значит, a – b = mt₁ .

Сравнения дают удобный язык для изучения делимости чисел. Связь сравнений с делимостью выявлена в свойстве 2⁰.

Примеры: 1. Докажите, что если a при делении на 23 даёт остаток 5, то a⁴ – 8a³ + 19 даёт остаток .

Действительно, если a  5 (mod 23), то

a⁴ – 8a³ + 19  (a²)² – 8aa² + 19  2² – 852 + 19 

 – 402 + (2² + 19)  –(–6)2 + 0  12 (mod 23),

т.е. остатком будет 12.

2. Вычислить 18¹⁰⁰ + 20 (mod 25).

18¹⁰⁰ + 20  (–7)²⁵ – 5  –(7²)¹²7 – 5  –7(–1)¹² – 5 

 –7 – 5  –12  13 (mod 25).