Лекция № 20.

4.7. Производная обратной функции

Теорема. Пусть функция монотонна в некоторой окрестности точких и , тогда обратная функциятакже имеет производную в соответствующей точкех, которая определяется по формуле

. (1)

Действительно, в силу монотонности функции для приращенияи тогда

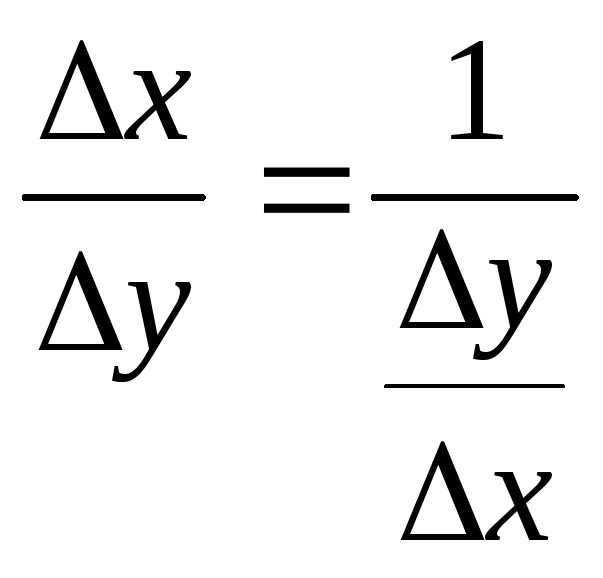. (2)

Если , то в силу непрерывности, и, переходя к пределу в выражении (2), получаем формулу (1).

Пример 1. Найти , если.

Обратная к этой функции есть функция и тогда по формуле (1) получаем

.

Для функции имеем

.

Аналогично можно доказать формулы (10-11) таблицы производных.

4.8. Производная функции, заданной параметрическими уравнениями

Пусть функция задана параметрическими уравнениями

тогда справедлива следующая

Теорема. Если функции являются дифференцируемы-ми в соответствующей точке, то

.

Пусть функция имеет обратную функцию, тогда функцияявляется сложной функцией и по правилу дифференцирования сложной функции (4.6) получаем. Если воспользоваться формулой (1), то имеем

.

Пример 2. Составить уравнение касательной к линии при, т.е. в точке.

Имеем

,

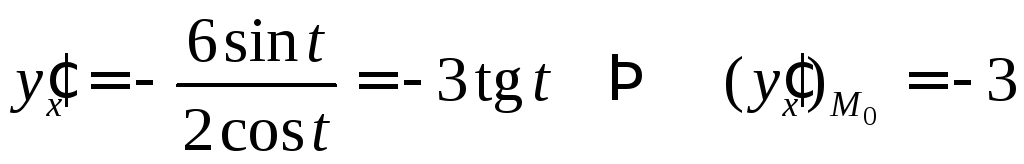тогда уравнение касательной

.

4.9. Производная функции, заданной неявно

Пусть функция задана неявно

(3)

Продифференцируем выражение (3) по аргументу х с учётом, что и разрешим полученное соотношение относительно. Покажем эту процедуру на конкретном примере.

Пример 3. Найти , если.

.

4.10. Производная степенно-показательной функции

Определение 1. Функция вида называется степенно-показательной.

Прологарифмируем эту функцию

. (4)

Дифференцируя обе части выражения (4), получим

или

(5)

Рассмотренная операция называется логарифмическим дифференциро-ванием. Формулу (5) можно удобно запомнить как сумму производных от показательной и степенной функций.

Пример 4. Найти , если.

Прологарифмируем .

Дифференцируя полученное равенство, окончательно имеем

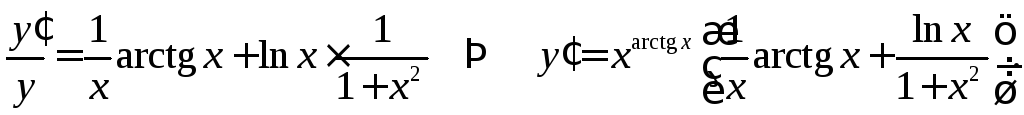
4.11. Производные высших порядков

Если функция дифференцируема, то функцияможет также быть дифференцируемой функцией, тогда производная от этой функции называетсявторой производной (или производной второго порядка) от функции и обозначается

или .

Вообще производной порядка п от функции называется первая производная от производной (п  1)-го порядка и обозначается

или .

Пример 5. Найти п-ю производную от функции .

.

Пусть функция задана параметрическими уравнениями

Тогда, как известно,

.

Таким образом, в этом случае можно для нахождения использовать следующие формулы:

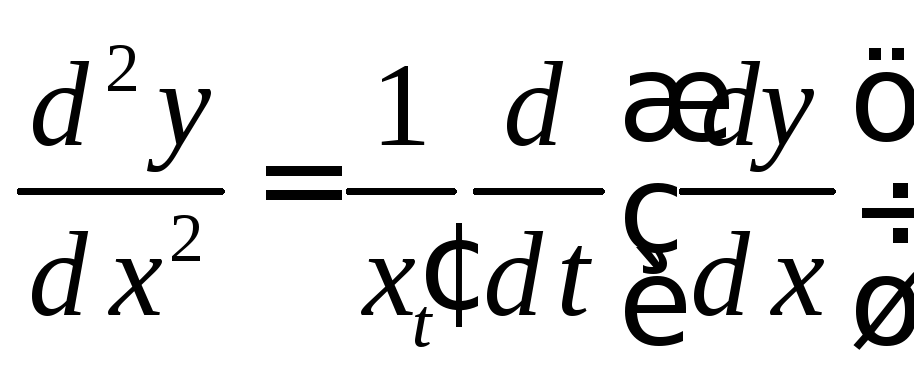. (6)

. (7)

Формулу (6) удобно использовать, если перед этим уже найдена .

Пример 6. Найти циклоиды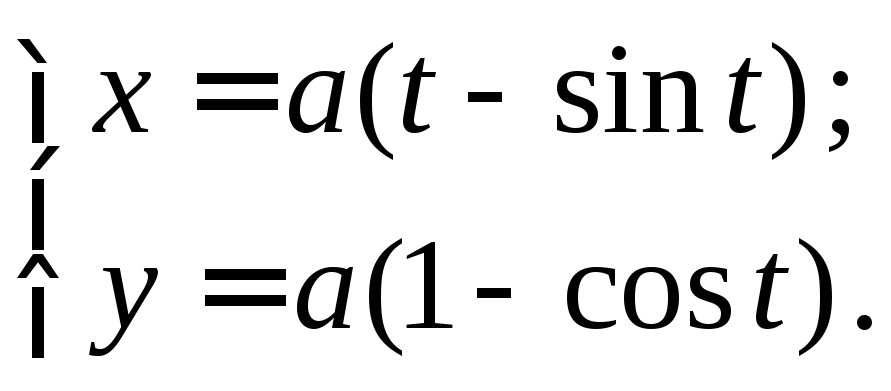

По формуле (7) получаем

.

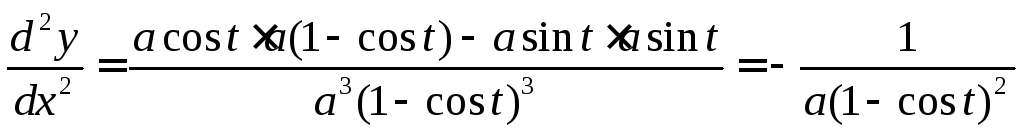Нахождение второй производной функции, заданной неявно, рассмот-рим на примере

Пример 7. Найти , если.

Продифференцируем это уравнение

.

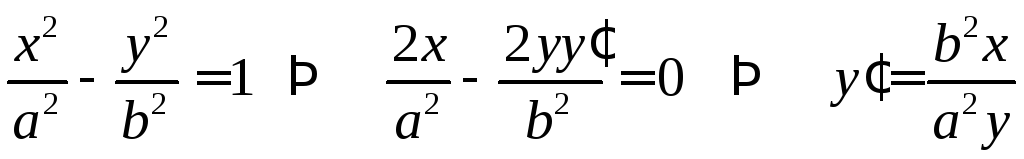Продифференцируем найденную первую производную ещё раз

.

С учётом выражения для и самой функции окончательно получим

.

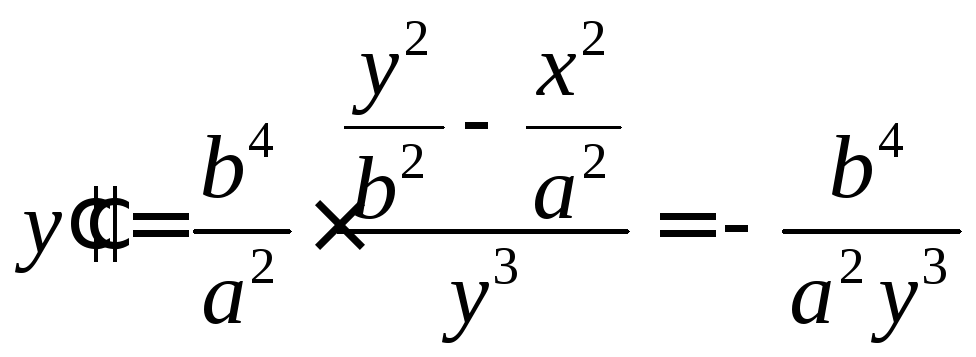Замечание 1. Аналогично можно находить производные высших поряд-ков от функций, заданных неявно или параметрическими уравнениями.

Замечание 2. Как и для производной первого порядка, можно рас-смотреть механический смысл второй производной, а именно, если  путь, пройденный материальной точкой, то ускорение .