6.2. Поверхности второго порядка
Пусть в некоторой ДСК задана поверхность, определяемая уравнением второй степени
(2)
где коэффициенты
одновременно не равны нулю. Эта поверхность
называется поверхностью второго
порядка.
Рассмотрим частные случаи уравнения (2):
1.
Эллипсоид.
Его каноническое уравнение
.
Чтобы составить
представление об этой поверхности,
проведём сечения плоскостями, параллельными
координатным плоскостям. Предварительно
заметим, что при замене
уравнение эллипсоида не изменяется –
это означает, что эта поверхность
симметрична относительно координатных
плоскостей.
Например, пересекая
эллипсоид плоскостями
,
получаем в сечениях эллипсы вида
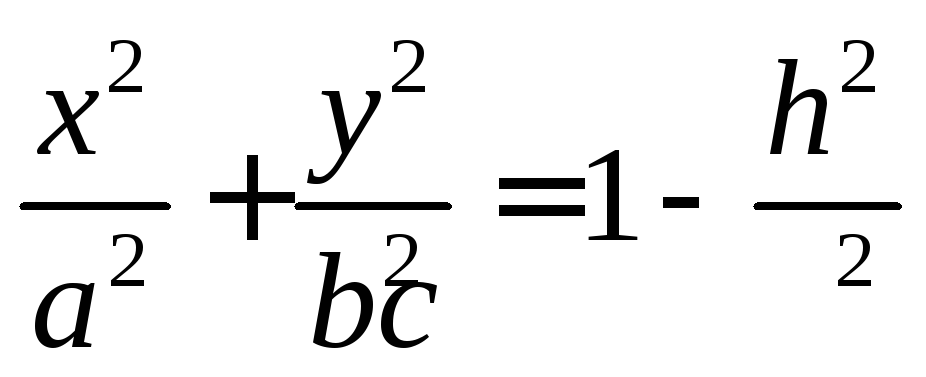
с полуосями
.
Отсюда видно, что
самый большой эллипс получается в
сечении
а при увеличении h
эллипсы уменьшаются, вырождаясь в
точ-ку при
.
А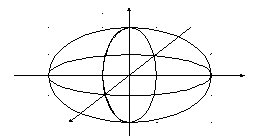
налогичная
картина будет в сечениях плоскостями
и
.
На основании таких исследований можно
определить окон-чательный вид эллипсоида.
z
c
a
b b y
a
x c
Так же можно получить вид следующих поверхностей:
2
.Однополостный
гиперболоид
z
y
x
3
.Двуполостный
гиперболоид
z
y
x
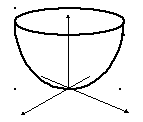
4. Эллиптический параболоид
.
z
x y
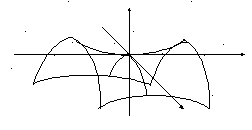
5. Гиперболический
параболоид
.
z
x
y
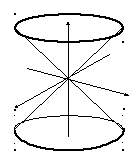
6. Конус
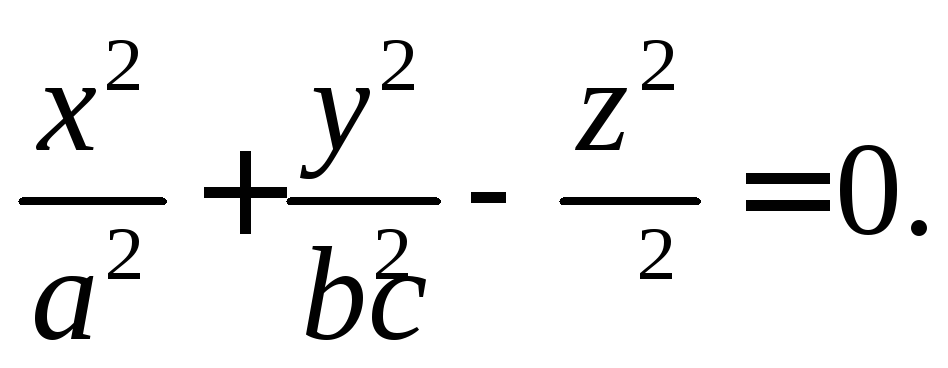z
y
x
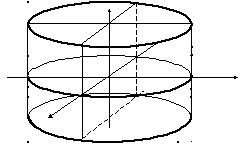
7.
Эллиптический
цилиндр
-
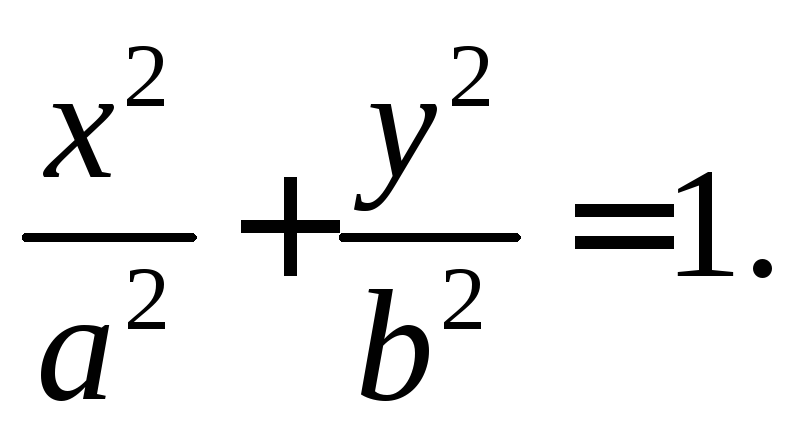
z
b у
a
x
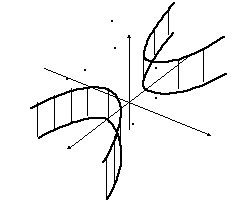
8.
Гиперболический
цилиндр
-
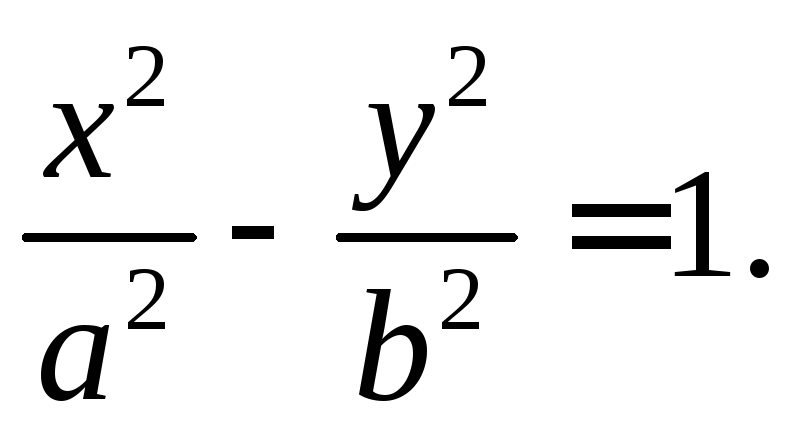z
-a
a
y
x
9. Параболический цилиндр -
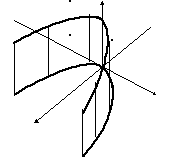
z
у
x
1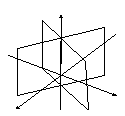
0.Пара
пересекающихся плоскостей
-
z
або
.
y
x
11. Пара
параллельных плоскостей
или
.
12. Пара
совпадающих плоскостей
.
13. Точка
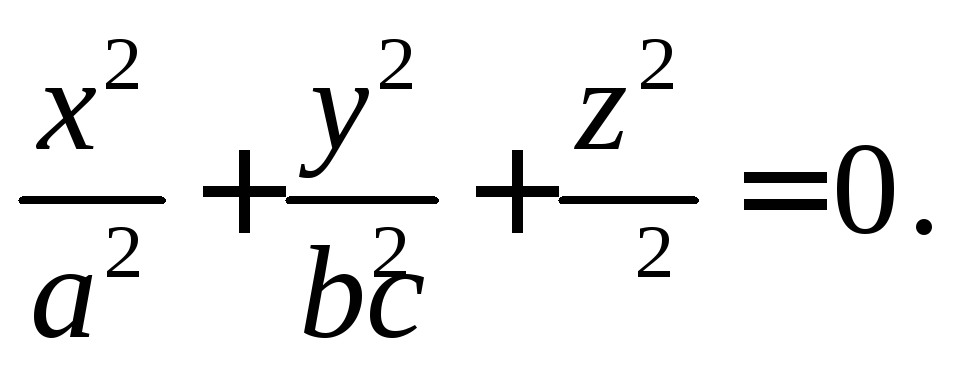
Аналогично, как и для случая линий второго порядка, имеет место
Теорема. Для любого уравнения (2) поверхности второго порядка существует такая декартовая система координат, в которой уравнение принимает один из видов (113).
Пример 3.
Найти точки пересечения прямой
с однополостным гиперболоидом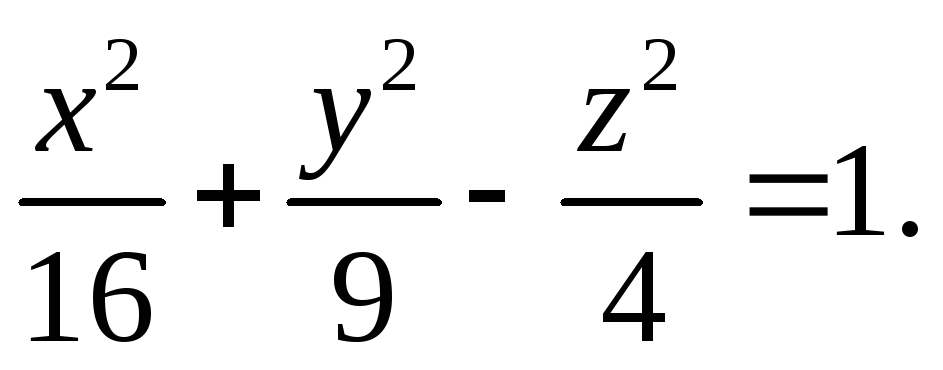
Прямую
представим
параметрическими
уравнениями
Под-
ставим
в уравнение гиперболоида, получим
уравнение для нахож-дения параметраt:
.
Его корни:
.
Это означает, что имеются две точки
пересечения прямой с гиперболоидом:
и
.
Какие еще могут быть варианты взаимного расположения прямой с однополостным гиперболоидом?