1.3. Элементарные функции

К основным или простейшим элементарным функциям относятся:

1. Степенная где.

2. Показательная .

3. Логарифмическая .

4. Тригонометрические: .

5. Обратные тригонометрические: .

В качестве повторения постройте графики этих функций.

Применяя к этим функциям арифметические действия и операцию суперпозиции конечное число раз, будем получать новые более сложные функции, которые называются элементарными.

Например, .

Иногда полезно использовать так называемые гиперболические функ-ции, которые также относятся к элементарным:

.

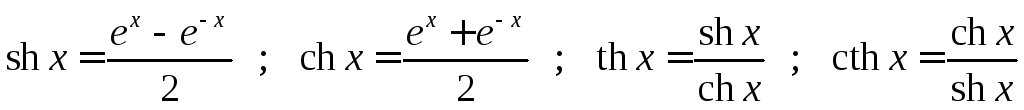Легко непосредственно проверить следующие их свойства:

.

Можно заметить, что эти свойства напоминают свойства тригоно-метрических функций, поэтому они соответственно и называются гипер-болическими синусом, косинусом, тангенсом и котангенсом.

Остальные функции относятся к так называемым неэлементарным. Примеры неэлементарных функций:

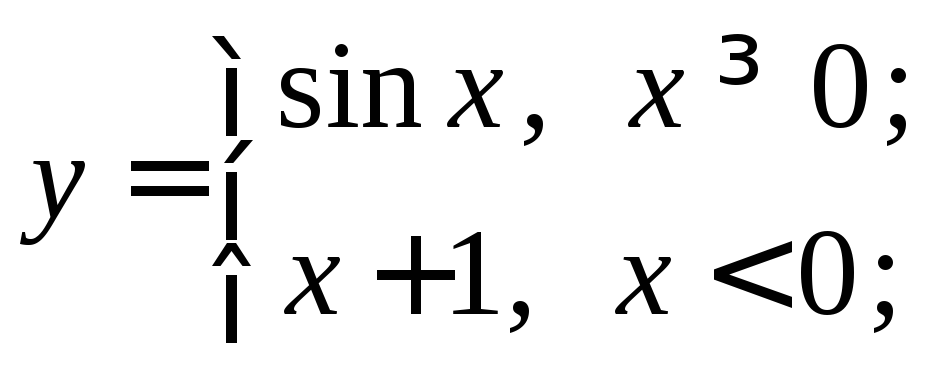
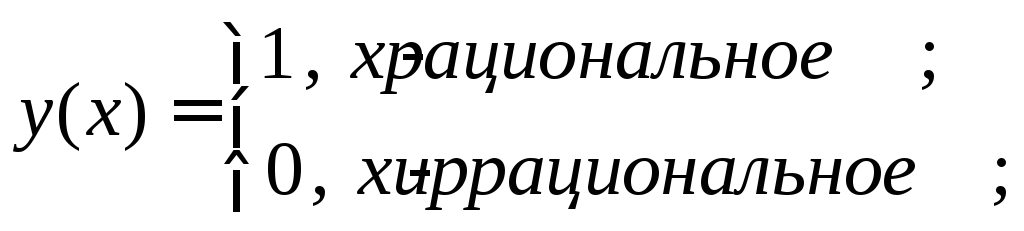функция Дирихле;

целая часть числа, где x  наибольшее целое число, не превосхо-дящее x, например,

Лекция № 15. Тема 2 : Пределы

2.1. Предел последовательности и переменной величины

Определение 1. Значения функции натурального аргумента , гденазываются последовательностью, которая обозначается

.

Примеры последовательностей:

1. .

2. . 3. .

Определение 2. Последовательность называетсяограниченной сверху (снизу), если существует такое число M(m), что любой член x_n этой последовательности удовлетворяет неравенству . Если последовательность ограничена сверху и снизу, то она называетсяограниченной.

Например, последовательность 1 является возрастающей и ограничен-ной, последовательность 2 возрастающая и ограничена снизу, а после-довательность3ограничена.

Определение 3. Число а называется пределом последовательности или пределом переменной величиныx_n , если , чтои пишут

или .

Дадим геометрическое представление предела  так как что выглядит следующим образом

( )

а х

Таким образом, если а предел последовательности , то, чтовсееечлены,начинаяснекоторого попадут в эту окрестность.

Пример 1. Покажем, что предел первой последовательности равен 1, т.е. .

Зададим произвольное и составим неравенство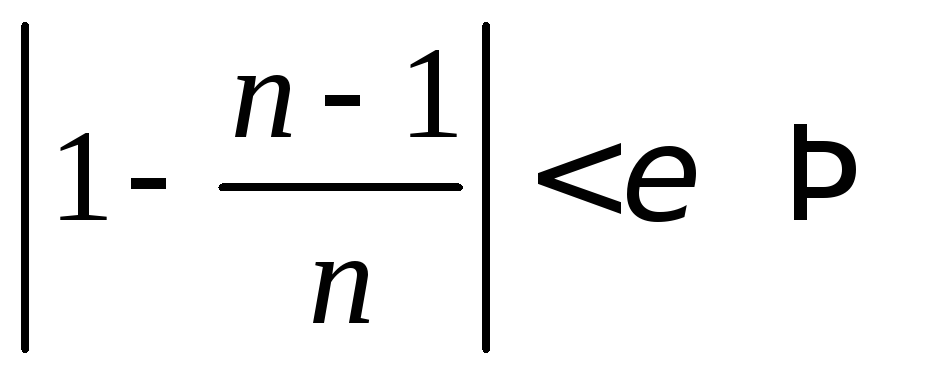, т.е.. Тогда номер члена, начиная с которого все члены последовательности попали в окрестность, определится из условия. Например, если , то, начиная с номера, все члены последовательности удовлетворяют неравенству или попали в окрестность.

Определение 4. Переменная x_n называется бесконечно большой при , если, чтои при этом пишут

или , еслии

или , если.

Пример 2. Покажем, что для второй последовательности .

Зададим и составим неравенство. Тогда неравенство выполняется, где.

Особое внимание следует уделить замечанию:

Замечание 1. Концептуально такие же определения и свойства имеют место и для любой переменной величины х. Например, число а называ-ется пределом переменной величины х, если , чтои пишутили, т.е. последовательность пред-ставляет собой переменную величину, значения которой пронумерованы.

Из определения предела переменной следуют её свойства:

1. Если переменная имеет предел, то он единственный.

2. Предел постоянной равен этой постоянной.

3. Если переменная имеет предел, то она ограничена.

4. Не всякая переменная имеет предел (см. последовательность 3 и задайте ).

5. Монотонная ограниченная переменная имеет предел.