3.2. Гипербола

Каноническое уравнение гиперболы имеет вид

т.е. в уравнении (1) нужно положить

Коэффициенты а и b называются соответственно вещественной и мнимой полуосями.

Положив , отметим на осиОх точки называемыефокусами гиперболы. Тогда гиперболу можно определить как

геометрическое место точек, разность расстояний от которых до фокусов по абсолютной величине равна 2а, т.е.

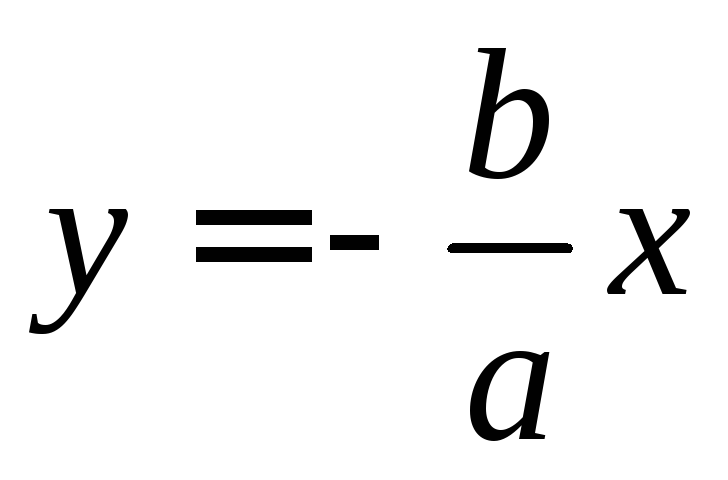у

К М

F₁ -а О а F₂ х

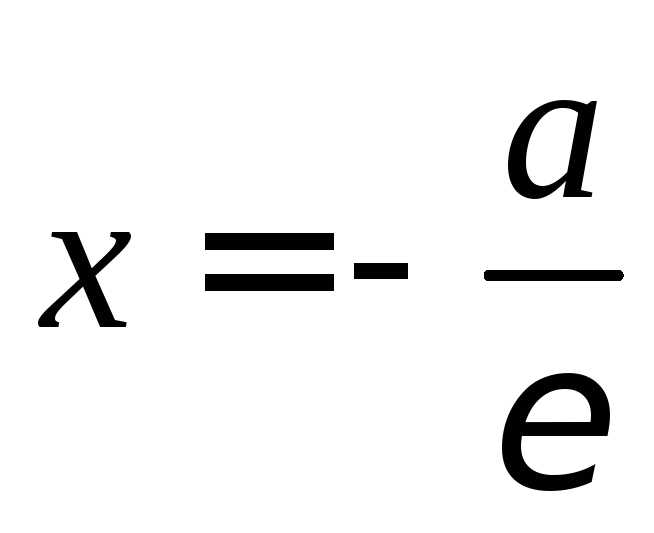
Доказывается аналогично, как и для эллипса. По виду уравнения гиперболы так же заключаем, что её график симметричен относительно осей системы координат. Часть гиперболы, лежащая в первой четверти, имеет уравнение Из этого уравнения видно, что при достаточно большихх гипербола близка к прямой . После схематичного построения в первой четверти симметрично отобра-жаем график во все четверти.

Точки называютсявершинами гиперболы. Прямые называютсяасимптотами – это прямые, к которым стремятся ветви гиперболы, не пересекая их.

Отношение называетсяэксцентриситетом гиперболы. Для гиперболы .

Прямые называютсядиректрисами гиперболы. Для директрис гиперболы имеет место свойство, аналогичное, как и для директрис эллипса.

Отношение расстояний от фокуса и директрисы для точек эллипса есть величина постоянная, равная эксцентриситету, т.е.

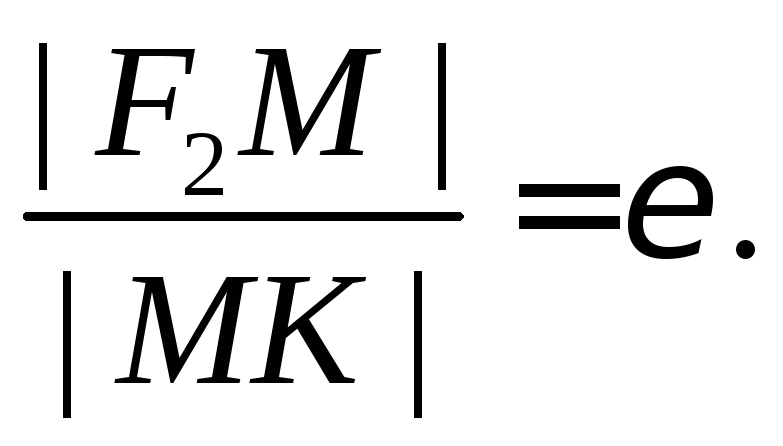
Пример 1. Найти уравнение эллипса, вершины которого находятся в фокусах, а фокусы в вершинах гиперболы .

Разделим обе части уравнения гиперболы на 144 и перейдем к каноническому виду

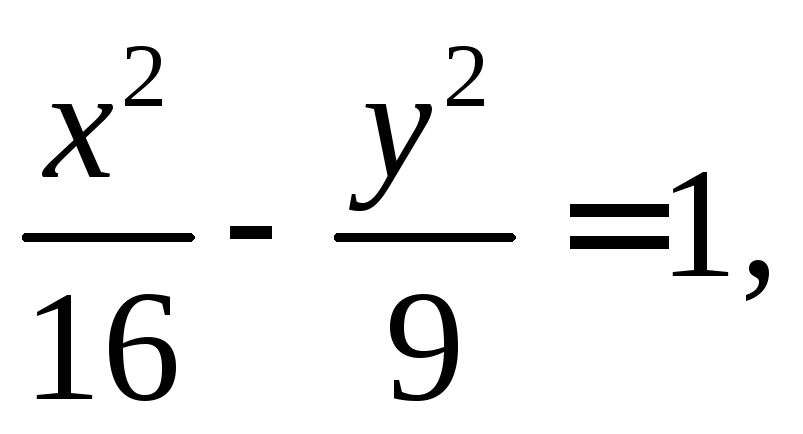
По условию а

Окончательно получаем

3.3. Парабола

Парабола определяется каноническим уравнением т.е. в уравнении (1) нужно положить

Коэффициентр называется К у

фокальным параметром. М

Отметим на оси Ох точку

называемую фокусом

параболы и проведём прямую, О F х

, называемую директрисой.

Тогда парабола может быть также определена как

геометрическое место точек, равноудалённых от фокуса и директрисы .

Действительно, для произвольной точки параболы имеем

и

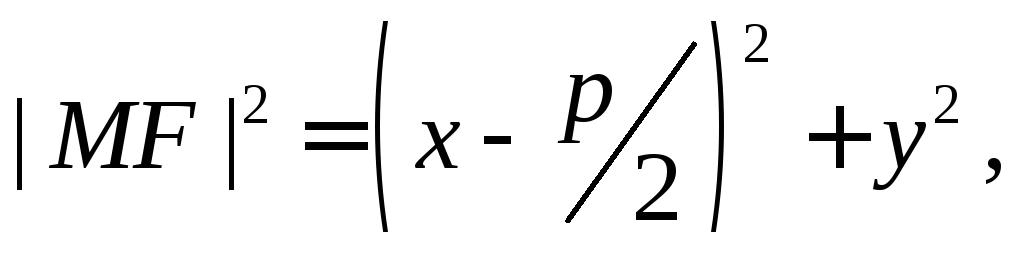
откуда и следует искомое равенство

3.4. Классификация линий второго порядка

В математике доказывается следующая

Теорема. Любое уравнение вида (1), если не рассматривать случай “мнимых“ линий, путём преобразования системы координат можно привести к одному из следующих видов:

1)  эллипс;

2)  гипербола;

3)  парабола;

4)  пара пересекающихся прямых;

5)  пара параллельных прямых;

6)  пара совпадающих прямых;

7)  точка.

Линии второго порядка классифицируются и по значению эксцентри-ситета:

эллипс;

парабола;

гипербола.