Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть 1

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

lim	Dy	=	lim	æ
	Dx			ç F¢(u0 )j¢(x0 ) + F¢(u0 )
Dx®0			Dx®0è

o(Dx)	+	o(Du) ö
			÷ .
Dx
		Dx ø

Первое слагаемое под знаком предела в правой части – это постоянная. Второе –

произведение постоянной на бесконечно малую, ибо lim						o(Dx)	= 0 по
произведение постоянной на бесконечно малую, ибо lim						Dx	= 0 по
					Dx®0	Dx
определению символа o(×). Третье слагаемое представим в виде
	o(Du)	=	o(Du)	×	Du .
	Dx	=		×	Du .
	Dx		Du		Dx

Здесь первый множитель есть бесконечно малая при Dx ® 0, а второй имеет конечный предел u¢(x0 ). Итак, второе и третье слагаемое – это бесконечно малые

при Dx ® 0. Отсюда и получаем формулу дифференцирования сложной функции.

Замечание 1. Остальные правила дифференцирования приведем позже.

§6. Производные основных элементарных функций

I Степенная функция y=xa

Dy =

DDyx =

Находим приращение функции и составляем разностное отношение:

		a		- x		a	æ		æ	+	Dx ööa
(x + Dx)				- x			= ç xç1			+	÷÷
							è		è		x øø
æ		+	Dx öa				-1
ç1		+			÷		-1
xa ×	è			x	ø			.
xa ×				Dx				.
				Dx

- x	a	= x	a	æ	æ	+	Dx öa
- x		= x		ç	ç1	+	÷
				ç	è		x ø
				è	è		x ø

-1÷÷;

Вычислим предел этого разностного отношения, используя эквивалентность для

степенной функции (1+ a)m -1~ ma при a ® 0:

lim Dy = lim ç xa

Dx®0 Dx Dx®0çç

Dx öa

-1

a × Dx

ç1

= xa lim

= xa ×

= a × xa -1.

Dx®0

Итак, имеем

(xa )¢ = a × xa -1.

(1)

Замечание 1. Вывод последней формулы предполагает, что x ¹ 0. Вычислим f+¢(0) (считаем, что a > 0, следовательно, 0Î D(y)):

- 52 -

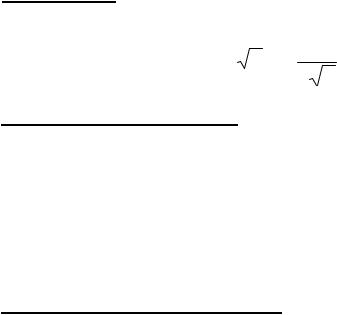
f ¢(0) = lim		f (0 + Dx) - f (0)		= lim (0 + Dx)a - 0a			= lim (Dx)a -1 .

+	Dx®0	Dx		Dx®0	Dx		Dx®0
Величина этого		предела	зависит от		a : для	a >1- f+¢(0) = 0, для

a = 1- f+¢(0) = 1 и для 0 < a < 1- f+¢(0) = +¥. Но этот же результат можно получить из формулы (1) с помощью теоремы 2 §3. Аналогичный результат можно получить и для f-¢(0), если a таково, что степенная функция определена

для x < 0.

Замечание 2. Ряд частных случаев формулы (1) лучше запомнить как

самостоятельные формулы дифференцирования:

ö¢

(x)¢ = 1, ( x)¢ =

÷ = -

è x

Показательная функция y=ax

lim

= lim

ax+Dx - ax

lim

ax (aDx

-1)

= ax

lim

Dx ln a

= ax ln a.

Dx®0

Итак,

(ax )¢ = ax ln a .

Частный случай этой формулы: (ex )¢ = ex .

III Логарифмическая функция y = ln x

x + Dx

Dx ö

ln(x + Dx) - ln x

lnç1+

lim

= lim

x ø

= lim

Dx®0

Dx x

Итак,

(ln x)¢ = 1x .

Для логарифмической функции с произвольным основанием используем формулу перехода:

		loga x =	ln x	.

	1		ln a
Отсюда (loga x)¢ =		.
	x ln a

Можно предложить и другой способ вычисления (ln x)¢ с использованием
основного логарифмического тождества				eln x = x. Продифференцировав
почленно это тождество, получим:

(eln x )¢ = x¢ Þ eln x × (ln x)¢ = 1Þ x(ln x)¢ = 1.

- 53 -

Отсюда и получим (ln x)¢ = 1x .

IV Тригонометрические функции

1. y=sin x

Dy = sin(x + Dx) - sin x = 2sin	Dx	æ	Dx ö
Dy = sin(x + Dx) - sin x = 2sin	2	×cosç x +	÷ .
	2	è	2 ø

æ Dx ö

Dx ö

sinç

÷cosç x +

cosç x

lim

= 2 lim

2 ø

= 2 lim

2 ø

Dx®0

Dx ö

= cos x

= lim cosç x +

Dx®0

(на последнем шаге мы воспользовались непрерывностью косинуса). Итак,

(sin x)¢ = cos x .

Производные остальных тригонометрических функций можно вычислить, используя определение производной, но проще использовать известные правила дифференцирования и формулы, связывающие тригонометрические функции друг

сдругом.

2.y=cos x

- x

= cosæ

- x

= sin x ×(-1) .

(cos x)¢ = çsinæ

è 2

øø

è 2

Итак,

(cos x)¢ = -sin x .

3. y=tg x

æ sin x ö¢		cos x × cos x - sin x × (-sin x)			1
(tgx)¢ = ç	÷ =			=				.
(tgx)¢ = ç	÷ =	cos2 x		=		cos2	x	.
è cos x ø		cos2 x				cos2	x
Итак,
		(tgx)¢ =	1		.
		(tgx)¢ =	cos2 x		.
			cos2 x

4. y=сtgx.

Аналогично предыдущему можно получить

(ctg x)¢ = - sin12 x .

- 54 -

Dx ® 0

стремится к

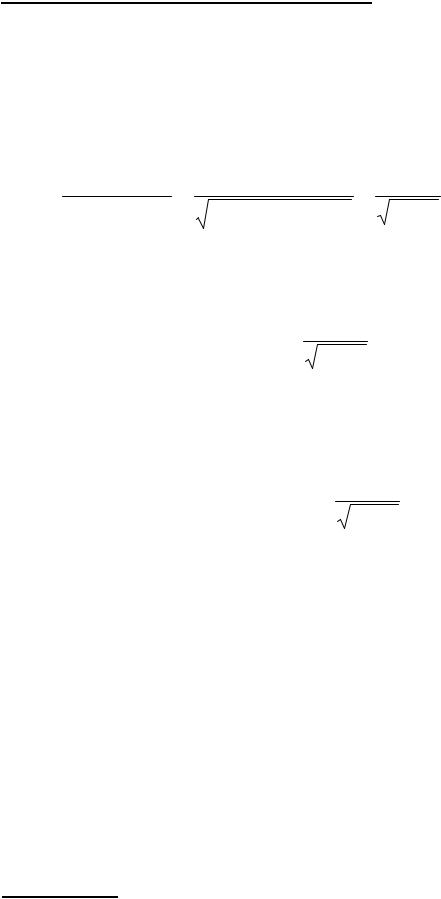
V Обратные тригонометрические функции

Производные этих функций проще всего получить при помощи основного тождества, связывающего пару взаимно обратных функций, а именно:

f ( f -1(x)) = x .

1. y=arcsin x

Дифференцируем почленно тождество sin(arcsin x) = x :

(sin(arcsin x))¢ = (x)¢ Þ cos(arcsin x) × (arcsin x)¢ = 1Þ

1		1		1
(arcsin x)¢ = cos(arcsin x)	=	1- sin2 (arcsin x)	=	1- x2

(напомним, что arcsin x Î é- p ,p ù , поэтому cos(arcsin x) ³ 0).

ê ú ë 2 2 û

Итак,

(arcsin x)¢ =

1- x2 .

2. y=arccos x

arcsin x + arccos x = p

Известное соотношение

формула

для (arcsin x)¢, позволяют получить

(arccos x)¢ = -

1- x2 .

3. y=arctg x

(tg(arctg x))¢ = x¢

× (arctg x)¢ = 1Þ (arctg x)¢ =

cos2 (arctg x)

= cos2 (arctg x) =

1+ tg2 (arctg x)

1+ x2

Итак,

(arctg x)¢ =

4. y=arcctg x

+ x2

Из соотношения arctg x + arcctg x = p

, получим

(arcctg x)¢ = -

+ x2

Замечание

3. Покажем

на

примере

y = arctg x

как можно

получать

производные аркфункций, исходя из определения производной. Приращение арктангенса Dy = arctg(x + Dx) - arctg(x) 0 при (в силу

- 55 -

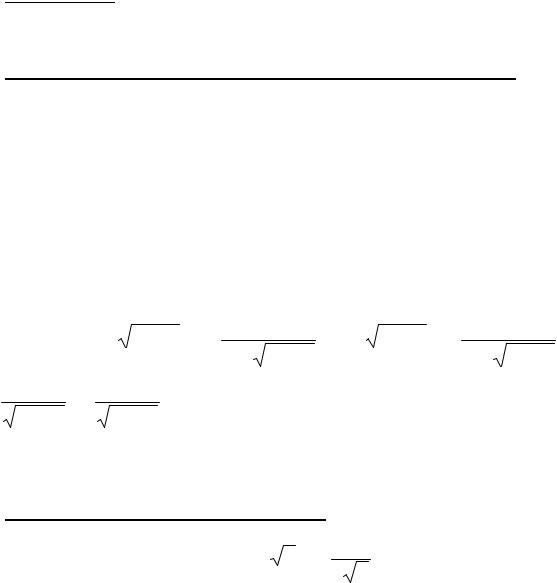
непрерывности

функции). Отсюда получаем эквивалентность:

при

Dx ® 0

tg(arctg(x + Dx)) - tg(arctg x)

(x + Dx) - x

Dy ~ tg(Dy) =

+ tg(arctg(x + Dx)) × tg(arctg x)

1+ (x + Dx)x

1+ x2 + x × Dx

Теперь можно легко найти предел разностного отношения:

	Dy		tg(Dy)			Dx
								1
lim		= lim		= lim	1+ x2 + x × Dx =				.
	Dx		Dx				1+ x2
Dx®0		Dx®0		Dx®0		Dx

Замечание 4. Производные аркфункций можно получить также, используя общее правило дифференцирования обратной функции, которое будет приведено ниже.

VI Гиперболические и обратные гиперболические функции

Эти функции элементарным образом выражаются через показательную и логарифмическую функции. Поэтому проще всего находить их производные, используя известные правила дифференцирования.

Например:

æ ex - e

-x ö¢

(ex

- e-x )¢(ex + e-x ) - (ex - e-x )(ex + e-x )¢

(thx)¢ = ç

-x

+ e

-x ÷

+ e

)

è e

(ex + e-x )2 - (ex - e-x )2

;

(ex

+ e

-x )2

(ex + e-x )2

ch2 x

(Arsh x)¢ = (ln(x +

x2 +1))¢ =

(x + x2 +1)¢ =

x + x2

x2 +1

x +

× (1+

x2 +1) =

x2 +1.

Производные других функций этой группы студентам предлагается получить самостоятельно.

VII Сводка формул для производных

)¢ = a × x

a -1

(x)¢ = 1

, ( x)¢ =

1 ö¢

1. (x

, ç

= -

2 x

è x ø

2. (ax )¢ = ax × ln a ,

(ex )¢ = ex .

3.	(ln x)¢ =	1 ,	(loga x)¢ =		1	.
					xln a
		x
4.	(sin x)¢ = cos x .					5. (cos x)¢ = -sin x .
6. (tg x)¢ =		1		.		7. (ctg x)¢ = -	1	.
		cos2	x				sin2 x

						- 56 -

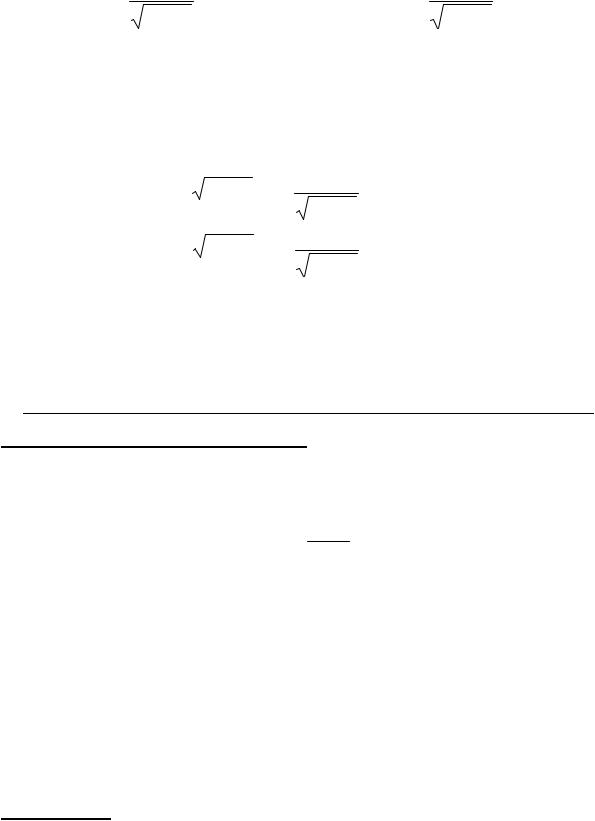
8. (arcsin x)¢ =					1						9. (arccos x)¢ = -						1
8. (arcsin x)¢ =				1- x2 .							9. (arccos x)¢ = -					1- x2 .
10.	(arctg x)¢ =				1		.				11. (arcctg x)¢ = -						1	.
10.	(arctg x)¢ =		1+ x2				.				11. (arcctg x)¢ = -				1+ x2			.
			1+ x2												1+ x2
12.	(sh x)¢ = ch x.										13. (ch x)¢ = sh x.
14.	(th x)¢ =	1			.						15. (cth x)¢ = -			1			.
14.	(th x)¢ =	ch2 x			.						15. (cth x)¢ = -			sh2 x			.
		ch2 x												sh2 x
16.	(Arsh x)¢ = (ln(x +							x2 +1))¢ =				1	.
16.	(Arsh x)¢ = (ln(x +							x2 +1))¢ =				x2	.
												x2	+1
17.	(Arch x)¢ = (ln(x +							x2 -1))¢ =				1	.
17.	(Arch x)¢ = (ln(x +							x2 -1))¢ =				x2	.
						1+ x ö¢						x2	-1
	(Arth x)¢ =		æ	1		1+ x ö¢				1
18.			ç		ln				÷ =			.
18.			ç	2	ln				÷ =	1- x2		.
			è	2		1- x ø				1- x2

§5 (продолжение). Основные правила дифференцирования

VII Логарифмическая производная

Пусть функция y = f (x) положительна и дифференцируема. Тогда и функция ln f (x) – дифференцируема, причем

(ln f (x))¢ = f 1(x) × f ¢(x) .

Это выражение и называется логарифмической производной функции f (x). Отсюда легко получить производную самой функции f (x):

f ¢(x) = f (x)×(ln f (x))¢.

Используя эту формулу можно получить правило дифференцирования сложной степенно-показательной функции:

	v(x)		v	æ	u¢ ö
y = (u(x))		Þ y¢ = y(ln u		)¢ = y × (v × ln u)¢ = y ×çv¢ln u + v ×		÷.
y = (u(x))		Þ y¢ = y(ln u		)¢ = y × (v × ln u)¢ = y ×çv¢ln u + v ×		÷.
				è	u ø

Окончательно имеем формулу:

(uv )¢ = uv lnu ×v¢ + vuv-1u¢.

Замечание 2. Вообще говоря, всегда лучше помнить не лишнюю формулу, а приём, который приводит к этой формуле. Для степенно-показательной функции можно предложить прием, использующий основное логарифмическое тождество:

	v		lnuv		vlnu		vlnu		v æ	u¢ ö
(u		)¢ = (e		)¢ = (e		)¢ = e		× (v ln u)¢ = u	çv¢ln u + v		÷.
(u		)¢ = (e		)¢ = (e		)¢ = e		× (v ln u)¢ = u	çv¢ln u + v		÷.
									è	u ø
							- 57 -

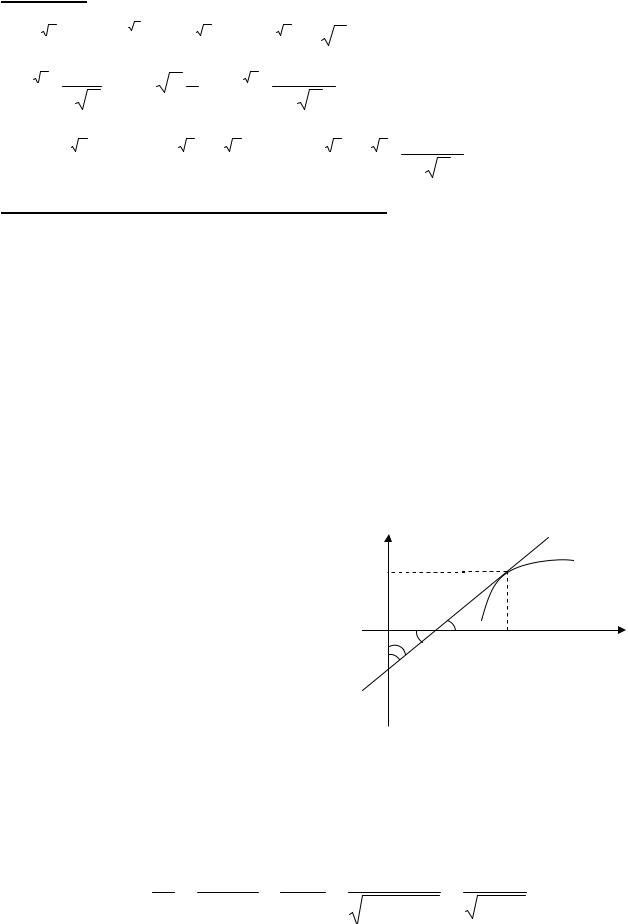
Примеры.

1. (x x )¢ = (eln x x )¢ = (e x ln x )¢ = e x ln x ( x ln x)¢ =

= x

x æ

ln x +

ln x + 2

÷ = x

è 2

2.(sin(x

x ))¢ = cos(x x )(x

x )¢ = cos(x x )(x

x ) ln x + 2.

2 x

VIII Дифференцирование обратной функции

Пусть функция

y = f (x) в некоторой окрестности точки x0 – непрерывная

и строго

монотонная, а

кроме

того, дифференцируема в точке

x0 , причем

f ¢(x0 ) ¹ 0 . Тогда в

некоторой

окрестности точки y0 = f (x0 )

существует

обратная

функция

x = g(y),

также непрерывная, строго монотонная и

дифференцируемая в точке y0 , причем

g¢(y0 ) =

(1)

¢(x0 )

Строгое доказательство приводить не будем, но дадим геометрическую иллюстрацию. При этом используем тот факт, что у графики взаимно-обратных функций y = f (x) и x = g(y) совпадают, а производная – это угловой

коэффициент касательной.

f ¢(x0 ) = tga ,

g¢(y0 ) = tgb = tgæp

èç 2

ö	=	y0	=f(x)
-a ÷	=
ø

= ctga = tga

= f ¢(x ) .

Формулу (1)

записывают еще в

виде

x¢

или y¢

x¢y

y¢x

Применим последнюю формулу для вычисления производной, например, арксинуса:

y = arcsin x Û x = sin y ,

y¢	= (arcsin x)¢ = 1	=	1	= 1 =	1	=	1 .
x	x¢y		(sin y)¢	cos y	1- sin2 y		1- x2
	x¢y		(sin y)¢	cos y	1- sin2 y		1- x2

- 58 -

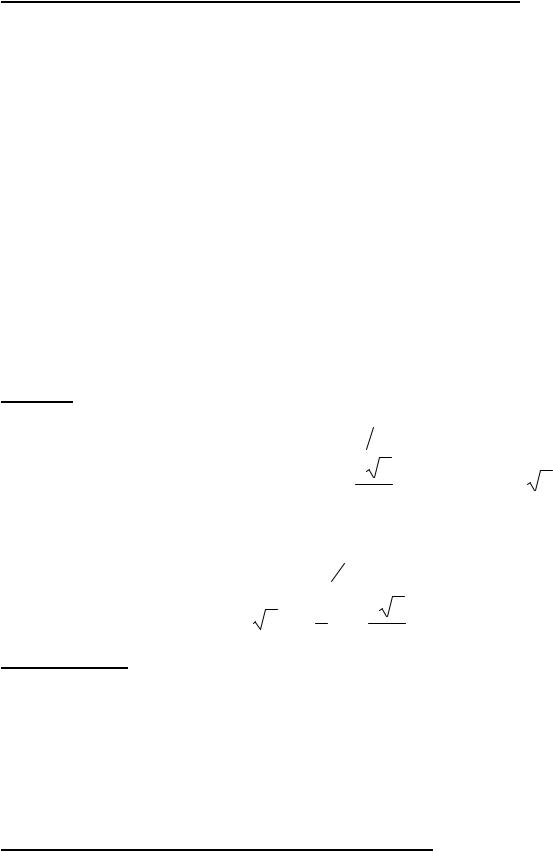
IX Дифференцирование функции, заданной параметрически

ìx = x(t),

t Î(a, b ),

Пусть имеется система параметрических уравнений í

причем функции x(t)и y(t) дифференцируемы и x¢(t)

îy = y(t),

сохраняет знак. Тогда на

области

значений

функции

x(t)

существует

дифференцируемая

функция

y = g(x), причем

y¢ =

y¢(t)

x¢(t)

Действительно, из условия

x¢(t) > 0 (или x¢(t) < 0) следует монотонность

функции

x = x(t);

следовательно, у неё

существует

обратная t = t(x). Тогда

y = y(t(x)) –

некоторая

функция

от x.

Её

производную можно найти, если

применить правила дифференцирования сложной и обратной функций:

y¢

= (y(t(x)))¢

= y¢(t(x))×t¢(x) = y¢(t)×

y¢(t)

x¢(t)

Пример.

ìx = 3cost

в точке

3. Составим уравнение касательной к эллипсу í

= p 4.

îy = 2sin t

M0 , соответствующей значению параметра

Координаты точки касания:

= 3cost

= 3

2 ,

= 2sin t

2 . Угло-

вой коэффициент касательной

= y¢

(2sin t)¢

= -

ctg p

= -

êàñ

t=t0

(3cost)¢

t=p

Искомое уравнение имеет вид:

y -

2 = -

2 (x -

3 2).

Замечание 3. Вообще говоря, производная функции, заданной параметрически, есть функция, заданная параметрически. Методически более правильным было бы писать такую производную в виде системы параметрических уравнений:

ì x = x(t),
ï			y¢(t)
íy¢		=	y¢(t)	.
íy¢		=		.
ï	x		x¢(t)
î			x¢(t)

X Дифференцирование функции, заданной неявно

При некоторых условиях, которые будут сформулированы в теме “Функции

нескольких переменных”, уравнение с двумя переменными вида	F(x, y) = 0
определяет y как функцию от x: y = y(x). Другими словами,	существует

- 59 -

функция y(x), обращающая уравнение в тождество. Производную этой функции

можно найти (в неявном же виде), не находя самой функции. Точные формулы будут даны позже, а сейчас сформулируем правило:

тождество F(x, y(x)) º 0 дифференцируем по x, не забывая, что y – это функция от x; затем из полученного равенства находим y¢x .

Примеры. 4. Дано: ey - xy + x2 = 0. Дифференцируем по x обе части:

(ey - xy + x2 )¢ = 0¢ Þ ey × y¢ - (1× y + x × y¢) + 2x = 0 . Þ y¢ = 2x - y .

x - ey

Выведем

уравнение

касательной

к эллипсу

= 1, проходящей

M0 (x0 , y0 ) .

через его точку

Найдем угловой коэффициент касательной. Для

этого уравнение эллипса дифференцируем по x, не забывая, что y = y(x):

2yy¢

= 0 Þ y¢ = -

b2 x

Þ k

= -

b2 x0

êàñ

a2 y

В общее уравнение касательной подставим найденный коэффициент и

преобразуем уравнение:

ö Þ

y = y

+ ç

÷(x - x )

Þ y = y

x +

è b

x x

x +

y =

Так как точка M0

принадлежит

эллипсу, то правая часть полученного

уравнения равна 1. Следовательно, искомая касательная имеет уравнение

x0 x

y0 y

= 1.

§7. Дифференциал функции

I Определение и геометрический смысл

Известно, что приращение дифференцируемой в точке x0 функции y = f (x) можно записать в виде суммы

Dy = f ¢(x0 ) × Dx + o(Dx)

двух слагаемых, каждое из которых стремится к нулю при Dx ® 0. Однако, второе слагаемое имеет порядок малости более высокий, чем первое (“быстрее” стремится к нулю). То есть в этой сумме главную роль играет первое слагаемое.

- 60 -

Определение. Главная часть приращения Dy функции y = f (x), линейная

относительно приращения Dx аргумента ции и обозначается символом dy.

Итак,

dy = f ¢(x0 )Dx .

Геометрический смысл виден из рисунка: дифференциал функции – это приращение ординаты касательной к графику функции, соответствующее приращению аргумента Dx .

x, называется дифференциалом функ-

y = f (x)		dy
y = f (x)


	Dx
x0	x0 + Dx

Дифференциалом независимой

переменной x, принято называть ее приращение Dx и обозначать dx: dx = Dx . Тогда формула для дифференциала функции приобретает симметричный вид

dy = f ¢(x0 )dx или dy = y¢dx.

II Инвариантность формы первого дифференциала

Правило дифференцирования сложной функции приводит к одному очень важному свойству дифференциала. Вычислим dy для функции y = F(x) в двух случаях:

1) x – независимая переменная, тогда dy = F¢(x)dx ; 2) x – некоторая функция x = j(t), тогда

dy = (F(j(t))¢dt = F¢(j(t))j¢(t)dt = F¢(j(t))(j¢(t)dt) = F¢(j(t))dj(t) =

= F¢(x)dx.

Сравнивая результаты, получаем т.н. свойство инвариантности формы первого дифференциала:

форма 1го дифференциала функции y = F(x) не зависит от того, является ли переменная x независимой или функцией другой переменной.

III Таблица дифференциалов

Так как дифференциал dy лишь множителем dx отличается от производной y¢x , то по таблице производных легко составить таблицу дифференциалов.

1. d(x

) = a × x

a -1

dx( x) =

1 ö

= -

dx ,

dxç

è x ø

- 61 -

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2016159.74 Кб8М_указания_к_практике_2_курс.doc
#
03.03.2016256.98 Кб27МАВ.docx
#
03.03.201657.3 Кб120макет учебного плана.docx
#
03.03.2016274.94 Кб13Макро Курс лекций.doc
#
03.03.2016144.9 Кб5маркет - заочн.doc
#
03.03.20161.71 Mб25МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть 1.pdf
#
03.03.20163.71 Mб77материаловедение 10 вариант.docx
#
03.03.2016136.19 Кб3МВ ДІ курсовий проект 2012 семестр 1.doc
#
03.03.2016296.96 Кб33МВ ДИ практ.doc
#
03.03.2016480.26 Кб11МВ ДИ сам.doc
#
03.03.20166.04 Mб7МД_gorn.pdf