
МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть 1
.pdf
f '(c1 ) - f '(x0 ) = f ''(c2 )(c1 - x0 ),c2 Î(x0 ,c1 ).
Итак, для разности ординат точки графика и точки касательной имеем равенство: yô - yk = f ''(c2 )(c1 - x0 )(x - x0 ). Возможны два случая взаимного
расположения точек x, x0 , c1, c2 :
x0 |
с2 |
с1 |
x |
x |
c1 |
c2 |
x0 |
В обоих случаях произведение |
(c1 - x0 ) × (x - x0 ) положительно, следовательно, |
||||||
sign(yô |
- yk ) = sign( f ''(x)): |
если f ''(x) ³ 0 , |
то |
yф ³ yk , т.е. график |
|||
расположен выше |
касательной, |
функция выпукла |
вниз; |
если |
f ''(x) £ 0 , то |
||
yф £ yk , график расположен ниже касательной, функция выпукла вверх. Теорема
доказана.
Замечание 1. Доказанная теорема имеет простую геометрическую иллюстрацию. Если функция выпукла вниз, то угловой коэффициент касательной, т.е. f '(x) возрастает, значит f ''(x) = ( f '(x))'> 0. Для выпуклой вверх
функции первая производная убывает, значит, вторая производная отрицательна.
Пример |
1. |
Исследовать |
на |
выпуклость степенную функцию |
f (x) = xa , x > 0. |
|
|
|
|
Имеем |
f ''(x) = a(a -1)xa -2 . |
Если a >1 или a < 0 , то f ''(x) > 0 , а |
||
если a Î(0,1) , то |
f ''(x) < 0 . Значит, |
f (x) = xa на луче (0,+¥) выпукла вниз |
||
при a < 0 и a >1, и выпукла вверх при 0 < a <1. При a = 0 или a =1 имеем линейную функцию f (x) = x или f (x) =1. Такие функции могут считаться как выпуклыми вверх, так и выпуклыми вниз.
II Точки перегиба
Определение 2. Точку M0 (x0 , f (x0 )) называют точкой перегиба графика функции y = f (x) , если она отделяет участки графика с противоположными
направлениями выпуклости.
Одно полезное свойство точки перегиба: если в точке перегиба существует касательная к графику функции, то она пересекает график.
Замечание 2. Часто это свойство принимают за определение точки перегиба. Но такое определение вовсе не равносильно данному выше. Кривая может и не иметь касательной в точке перегиба, а может случиться обратное: кривая пересекает касательную в точке, которая не отделяет участки с противоположными направлениями выпуклости. Примерами могут служить
- 82 -
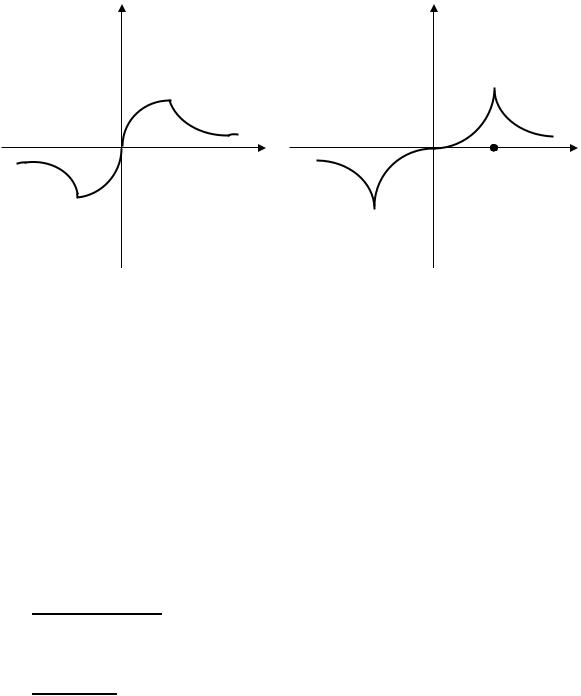
функции |
f (x) = arcsin |
|
|
2x |
и |
g(x) = (x + 2)2 / 3 |
- (x - 2)2 / 3 : у |
первой в |
|||
1 |
+ x2 |
||||||||||
|
|
|
|
|
|
|
|
||||
точках |
перегиба |
M1 (1;p ) |
и |
M2 (-1;- p ) |
нет |
касательных |
(хотя есть |
||||
|
|
|
2 |
|
2 |
|
прямые x = 2 |
и x = -2 |
|||
односторонние касательные), |
для |
графика второй |
|||||||||
являются касательными. |
|
|
|
|
|
|
|
|
|||
y
y
0,5π
0 |
|
0 |
|
1 |
x |
2 |
x |
Можно привести и более интересный пример:
ì |
5 |
æ |
|
2 |
æ 1 |
ö |
ö |
|
ïx |
|
ç1 |
+ sin |
|
ç |
|
÷ |
÷, x ¹ 0, |
|
|
|
||||||
h(x) = í |
|
è |
|
|
è x |
ø |
ø |
|
ï |
|
|
|
|
|
|
||
î |
|
|
0, x = 0. |
|||||
График этой функции в начале координат касается оси 0x и пересекает её; здесь существует непрерывная вторая производная, но она бесконечное множество раз меняет знак в окрестности нуля. (Предоставляем читателю самому провести все необходимые вычисления для этих функций).
Приведём без доказательств ряд теорем, в которых используется понятие критической точки второго порядка.
Определение 3. Точка x0 называется критической точкой второго порядка функции f (x) , если вторая производная функции в этой точке равна нулю или не существует.
Теорема 2 (необходимое условие точки перегиба). Если M0 (x0 , f (x0 )) – точка перегиба функции f (x) , то x0 – критическая точка второго порядка.
- 83 -

Теорема 3 (первое достаточное условие точки перегиба). Пусть x0 – критическая точка второго порядка непрерывной функции y = f (x) и пусть существует d > 0 такое, что в окрестностях (x0 -d , x0 ) и (x0 , x0 + d ) вторая производная f ''(x) существует и имеет противоположные знаки. Тогда точка
M0 (x0 , f (x0 )) – точка перегиба графика функции y = f (x) . |
|
|
||||||||||||||||||||||||
Теорема 4. |
(второе достаточное условие точки перегиба). Если функция |
|||||||||||||||||||||||||
y = f (x) |
имеет |
в точке |
x0 |
конечную |
|
|
производную |
третьего |
порядка и |
|||||||||||||||||
удовлетворяет условиям f ''(x0 ) = 0 |
, |
|
f '''(x0 ) ¹ 0, |
то |
график этой |
функции |
||||||||||||||||||||
имеет перегиб в точке M0 (x0 , f (x0 )) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 2. |
Найти |
интервалы |
|
|
выпуклости и |
точки перегиба |
функции |
|||||||||||||||||||
f (x) = |
|
x -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. В предыдущем параграфе мы уже исследовали эту функцию на |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ì x - 2 |
, x < 1, x ¹ 0, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
||||||||||
экстремум и получили |
f '(x) = í |
2 |
- x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
ï |
|
, x > 1. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|||||||||
Находим вторую производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ì |
|
2 × |
|
|
x - 3 |
, x > 1, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
f ''(x) = í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ï |
|
3 - x |
, x < 1, x ¹ 0. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
î2 × x4 |
|
|
|
|||||||||||||
Напомним, что |
f '(x) |
не |
существует |
в |
точке x1 =1, |
значит, и |
f ''(x) не |
|||||||||||||||||||
существует в этой точке, т.е. эта точка – критическая точка второго порядка. Ещё одну такую точку найдём, решив уравнение f ''(x) = 0 : x2 = 3. Эти критические точки разбивают область определения D(y) = (-¥,0) È (0,+¥) на интервалы знакопостоянства второй производной, т.е. интервалы выпуклости самой функции. Знаки f ''(x) определяем так же, как и знаки f '(x) при исследовании на экстремум. Приходим к чертежу:
- 84 -
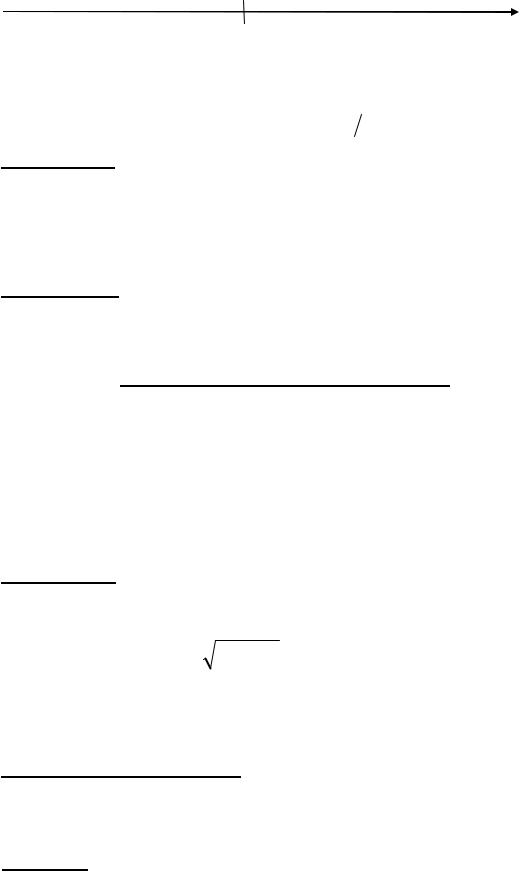
знак у'' |
+ |
+ |
– |
+ |
|
|
|||||
|
|
|
|
|
x |
|
0 |
1 |
3 |
|
|
Итак, имеем: на интервалах (-¥,0), |
(0,1) и (3,+¥) |
функция выпукла вниз, а на |
|||
(1,3) – выпукла вверх; точки M1 (1,0) и M2(3,2 9) |
– точки перегиба. |
||||
Замечание 3. В случае недифференцируемой функции принято другое |
|||||
определение выпуклости, а именно: |
функция f (x) |
называется выпуклой вниз |
|||
(вверх) на интервале |
(a,b), если все точки любой дуги её графика лежат под |
||||
(над) соответствующей хордой или на ней. Для дифференцируемой функции это определение равносильно данному выше.
Замечание 4. Третье достаточное условие перегиба будет дано в следующей теме.
§5. Асимптоты графика функции
Если функция имеет бесконечные разрывы или определена на бесконечном промежутке, то в силу конечности размеров чертежа приходится довольствоваться лишь частью всего графика. Асимптоты позволяют отчетливо представить себе вид графика и за пределами чертежа.
Будем говорить, что точка M (x, y) удаляется в бесконечность, если расстояние d (O, M ) от точки до начала координат неограниченно
увеличивается. |
|
p называется |
|
линии L, если |
||
Определение. |
Прямая |
асимптотой |
||||
расстояние от текущей точки M линии |
L до прямой p стремиться к нулю по |
|||||
мере удаления точки |
M в бесконечность. |
|
|
|
||
Расстояние d(0, M ) = |
x2 + y2 |
может |
стремиться |
в |
бесконечность |
|
различными способами: 1) x ® a, y ® ¥ |
; 2) x ® ¥, y ® b ; 3) |
x ® ¥ , y ® ¥. |
||||
В зависимости от способа и различают вертикальные, горизонтальные и наклонные асимптоты.
I Вертикальные асимптоты
Прямая x = a является вертикальной асимптотой графика функции y = f (x) , если хотя бы один из односторонних пределов функции в этой точке равен + ¥ или - ¥ (т.е. точка x = a – точка бесконечного разрыва).
Примеры. |
|
|
|
|
1. График функции f (x) = |
1 |
|
имеет асимптоту x =1, ибо |
|
x -1 |
||||
|
|
|||
- 85 -

f (1+ 0) = +¥, |
f (1- 0) = -¥ . |
||
2. |
Для графика логарифмической функции y = ln x ось ординат является |
||
асимптотой, ибо lim ln x = -¥ . |
|||
|
x®0+0 |
|
f (x) = exp(- x-1 . Для неё имеем: |
3. |
Рассмотрим функцию |
||
|
f (0 + 0) = |
lim |
exp(-1 x)= [exp(-1 (+0))]= [e-¥ ]= 0; |
|
|
x®0+0 |
|
|
f (0 - 0) = lim exp(-1 x)= [e+¥ ]= +¥ Þ прямая x=0 – |
||
|
|
x®0 |
-0 |
вертикальная асимптота.
Отметим, что график функции может иметь любое число вертикальных асимптот. График же элементарной функции не может пересекать свою вертикальную асимптоту
II Горизонтальные асимптоты
Прямая y = b является горизонтальной асимптотой графика функции
y = f (x) при |
x ® +¥ (x ® -¥) , если |
|
lim |
f (x) = b |
æ |
ö |
||
|
ç lim f (x) = b÷ . |
|||||||
|
|
|
|
x®+¥ |
|
è x®-¥ |
ø |
|
Примеры. |
|
|
|
|
|
|
|
|
4. |
Для |
графика показательной |
функции |
y = ax ось абсцисс |
является |
|||
асимптотой при x ® +¥, если a Î(0,1) , и при x ® -¥, если a >1. |
|
|||||||
5. |
Для графика y = arctg(x) прямая |
y = p – асимптота при x ® +¥, а |
||||||
|
y = - p – асимптота при x ® -¥. |
2 |
|
|
||||
прямая |
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
6. |
Для функции f (x) = sin x : |
lim sin x |
= [(б.м.) × (огр.)]= 0 |
, значит, |
||||
|
|
x |
x®±¥ |
x |
|
|
|
|
для этой функции ось абсцисс – асимптота и при x ® +¥, и при x ® -¥. Отметим, что график элементарной функции может иметь не более двух
асимптот: по одной на каждой из бесконечностей. Кроме того, график может
пересекать свою горизонтальную асимптоту (см. пример 6). |
|
|
III Наклонные асимптоты |
|
|
Теорема. Для того, чтобы график функции y = f (x) |
имел при x ® +¥ |
|
наклонную асимптоту y = kx + b , необходимо и |
достаточно, чтобы |
|
существовали конечные пределы |
lim (f (x) - kx)= b . |
|
lim f (x) x = k и |
(1) |
|
x®+¥ |
x®+¥ |
|
- 86 -

Доказательство. |
Запишем |
уравнение |
прямой y = kx + b в форме |
||||
p : kx - y + b = 0. Тогда |
можно |
воспользоваться готовой формулой для рас- |
|||||
стояния от точки графика M (x, f (x)) до прямой |
p : |
||||||
d(M , p) = |
kx - f (x) + b |
= |
1 |
f (x) - kx - b . |
|||
k 2 +1 |
k 2 |
||||||
|
|
+1 |
|
||||
Напомним ещё два результата из теории пределов:
lim F(x) = b Û lim [F(x) - b]= 0; |
|
|
|
|
||
x®a |
x®a |
|
|
|
|
|
lim [x × F(x)] = 0 Þ |
lim F(x) = 0, |
ибо |
F(x) = |
1 |
(x × F(x)). |
|
x®+¥ |
|
x®+¥ |
|
|
x |
|
Докажем необходимость. Пусть p : y = kx + b – асимптота. Значит,
d(M , p) ® 0 при x ® +¥, т.е. lim( f (x) - kx - b) = 0. Отсюда |
||||||||||||||
|
|
|
|
|
|
x®+¥ |
|
|
|
|
|
|
|
|
b = lim (f (x) - kx). С другой стороны |
|
|
|
|
|
|
|
|||||||
x®+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ f (x) |
|
b ö |
|||
|
lim ( f (x) - kx - b) = lim |
x ×ç |
|
- k - |
|
÷ = 0, |
||||||||
|
|
|
||||||||||||
|
x®+¥ |
|
|
|
|
x®+¥ |
|
è x |
|
x ø |
||||
|
æ f (x) |
- k - |
b ö |
= 0, а т. к. |
b |
® 0, то и lim |
æ f (x) |
|||||||
поэтому, |
lim ç |
|
÷ |
x |
ç |
|
||||||||
|
|
|||||||||||||
|
x®+¥è x |
|
x ø |
|
|
|
|
x®+¥è x |
||||||
Это же означает, что |
k = lim |
|
f (x) |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x®+¥ |
x |
|
|
|
|
|
|
|
|||
сразу имеем
-k ö÷ = 0.
ø
Докажем |
достаточность. Пусть |
существуют пределы (1). Тогда: |
|
lim (f (x) - kx)= b Û lim (f (x) - kx - b)= 0 Û lim d(M , p) = 0. |
По |
||
x®+¥ |
x®+¥ |
x®+¥ |
|
определению это и означает, что прямая |
y = kx + b , где k и b определены |
||
формулами (1), является асимптотой. Теорема доказана.
Замечание 1. Аналогично определяется наклонная асимптота для случая x ® -¥. Наклонных асимптот у графика элементарной функции может быть не более двух, причём горизонтальная асимптота – это частный случай наклонной. График может пересекать свою наклонную асимптоту.
Примеры.
7. Найдём асимптоты графика функции y = ln(1+ ex ).
lim ln(1+ ex ) = ln1 = 0 Þ y = 0 – асимптота при x ® -¥,
x®-¥
lim ln(1+ ex ) = +¥ Þ |
нет горизонтальной асимптоты при x ® +¥, но |
x®+¥ |
|
может быть наклонная: |
|
- 87 -
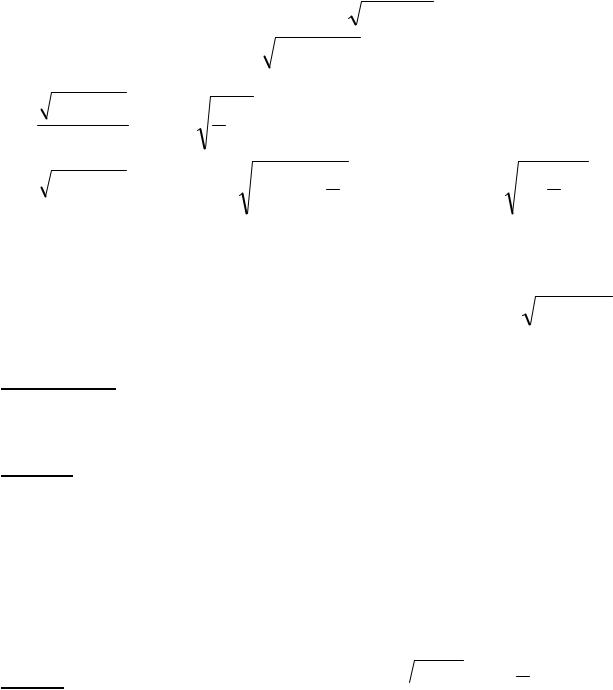
k = lim ln(1+ ex ) |
= é |
¥ |
ù = lim |
(ln(1+ ex ))' |
= lim |
ex |
|
=1; |
|
|
||
¥ |
x' |
1+ e |
|
|
|
|||||||
x®+¥ |
x |
ë |
û |
x®+¥ |
x |
|
|
|
|
|||
|
ê ú x®+¥ |
|
|
|
|
|
|
|||||
b = lim[ln(1+ ex ) - x]= lim[ln(1+ ex ) - ln ex ]= lim ln(1+ |
1 |
) = ln1 = 0. |
||||||||||
|
||||||||||||
x®+¥ |
|
|
|
x®+¥ |
|
x®+¥ |
|
|
e |
x |
||
Итак, прямая y = x – наклонная асимптота графика функции |
|
|
|
|||||||||
y = ln(1+ ex ) при |
||||||||||||
x ® +¥.
Заметим, что вертикальных асимптот график не имеет, ибо данная функция является непрерывной ( в силу элементарности ) на всей числовой оси.
8. Найти асимптоты графика функции |
y = 3 3x2 - x3 . Очевидно, что гори- |
||
зонтальных асимптот нет, ибо |
lim 3 |
3x2 |
- x3 = m¥. Далее, |
|
x®±¥ |
|
|
3 |
3x2 - x3 |
k = lim |
x |
x®±¥ |
|
b = lim (3 |
3x2 - x3 |
x®±¥ |
|
= lim |
3 3 |
-1 = -1; |
|
|
|
|
||
x®±¥ |
x |
|
|
|
|
|
|
|
+ x)= lim |
æ |
3 |
3 |
|
3 |
ö |
|
|
ç |
- x (1 |
- |
|
÷ |
= - |
|||
ç |
|
x |
) + x÷ |
|||||
x |
®±¥è |
|
|
|
ø |
|
||
= - lim x × |
1 |
æ |
- 3 |
ö |
=1. |
3 |
×ç |
x |
÷ |
||
x®±¥ |
è |
ø |
|
|
æ |
æ |
3 |
|
|
3 |
|
öö |
|
lim |
ç |
ç |
1 |
- |
|
-1 |
÷÷ |
= |
|
ç xç |
|
x |
÷÷ |
||||||
x®±¥è |
è |
|
|
|
|
øø |
|
||
Прямая |
y = -x +1 |
– наклонная асимптота графика функции y = 3 3x2 - x3 |
|||||||||||
при x ® +¥ и при x ® -¥. |
|
|
|
|
|
||||||||
Замечание |
2. |
Нетрудно заметить, что, |
если |
f (x) = kx + b + o(1) при |
|||||||||
x ® -¥( x ® +¥), |
то |
прямая |
y = kx + b – |
наклонная асимптота графика |
|||||||||
функции при x ® +¥( x ® -¥). |
|
|
|
|
|
||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|||
9. |
f (x) = 2x3 + x2 +1 = 2(x3 + x) + (x2 +1) - 2x |
= 2x +1- |
2x |
|
|||||||||
x2 +1 |
|||||||||||||
|
|
|
x2 +1 |
|
x2 +1 |
|
|
||||||
Так как |
lim |
2x |
|
|
= lim |
2x = 0, |
то прямая y = 2x +1 – асимптота графика при |
||||||
|
|
|
|||||||||||
|
x®±¥ x2 +1 |
|
x®±¥ |
x2 |
|
|
|
|
|
||||
x ® +¥ и x ® -¥.
Задача. Найти асимптоты графика функции y =  1+ x2 - x + 1x .
1+ x2 - x + 1x .
- 88 -
Лекция 14
§6. Общая схема исследования функции
На практике для построения графика функции y = f (x) иногда поступают так: из уравнения y = f (x) находят ряд точек графика и соединяют эти точки
плавной кривой. Однако, при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.
Для построения графика функции необходимо исследовать её свойства. Можно предложить следующую схему исследования функции y = f (x) , заданной явно.
1.Найти область определения, область непрерывности, точки разрыва, пределы в точках разрыва и в граничных точках D(y).
2.Найти асимптоты графика функции.
3.Вычислить производные y' и y'' и найти критические точки первого и второго порядка.
4. Составить таблицу изменения знака y' |
и y'' (к критическим точкам |
следует добавить точки разрыва и граничные точки |
D(y)). |
5. По знакам y' найти интервалы монотонности и точки экстремума. По знакам y'' найти интервалы выпуклости и точки перегиба.
6.Схематически изобразить в таблице поведение графика.
7.Нарисовать эскиз графика.
Замечания. а) Полезно исследовать функцию на четность и дичность. Чётную и нечетную функции достаточно исследовать лишь для а периодическую – на любом промежутке, длина которого равна периоду.
б) Полезно находить точки пересечения графика с осями координат.
в) Для уточнения поведения графика можно находить касательные в таких точках, как точки пересечения с осями координат, точки перегиба; в угловых точках находить односторонние касательные.
Пример. Исследовать функцию y = 3 3x2 - x3 и построить график. Решение. 1. D(y) = (-¥,+¥), функция всюду непрерывная, как элемен-
тарная.
2. Вертикальных асимптот нет, так как нет точек разрыва. В примере 8 предыдущего параграфа было установлено, что горизонтальных асимптот нет, а
прямая y = -x +1 является наклонной асимптотой при x ® +¥ и x ® -¥. 3. Вычисляем производные:
- 89 -
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
- |
1 |
|
|
|
|
|
|
1 |
|
1 |
- |
2 |
|
2 |
|
|||
y'= (3 3x2 - x3 )'= (x3 (3 - x)3 )'= |
x |
3 (3 - x)3 + |
|
× (-1) × x3 = |
|||||||||||||||||||||||||||||||||||||||||
3 |
|
3 |
(3 - x) 3 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
- |
1 |
|
|
|
- |
2 |
(2(3 - x) - x) = |
|
|
|
2 - x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3 |
x 3 (3 - x) 3 |
|
|
x |
× 3 |
|
(3 - x)2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
- |
1 |
|
- |
2 |
|
|
|
|
|
|
- |
1 |
|
|
- |
2 |
- |
1 |
- |
4 |
|
|
|
- |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y''= ((2 - x) × x |
|
3 (3 - x) 3 )'= -x |
|
3 (3 - x) |
3 |
3 |
x |
3 (2 - x)(3 - x) 3 - |
|||||||||||||||||||||||||||||||||||||
- |
2 (3 - x)-3 |
(-1)(2 - x)x-3 |
= x |
|
|
(3 - x)-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
-3 |
(-x(3 - x) - 1 (2 - x)(3 - x) + |
||||||||||||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
+ |
2 |
(2 - x)x) = |
|
|
|
- 2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
3 x4 × 3 (3 - x)5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Критические точки первого порядка: x1 = 2, x2 = 0, x3 = 3. Критические точки второго порядка: x2 = 0, x3 = 3.
4. Составляем таблицу изменения знака производных y' и y'' . Первая строка изображает D(y) с отмеченными критическими точками. Во второй и третьей строках отмечены знаки производных в интервалах, на которые
критические точки разбивают D(y). |
Четвёртая |
строка содержит графическое |
||||||
изображение поведения графика функции. |
|
|
|
|||||
x |
(-¥,0) |
0 |
(0,2) |
2 |
(2,3) |
3 |
(3,+¥) |
|
y' |
– |
± ¥ |
+ |
|
– |
- ¥ |
– |
|
y'' |
– |
не |
– |
– |
– |
не |
+ |
|
сущ. |
сущ. |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
т. max |
|
т. |
|
|
y |
|
т. min |
|
|
пере- |
|
||
|
y = 0 |
y = 3 4 |
|
гиба |
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
(3;0) |
|
|
График функции изображён на рисунке |
|
|
|
|
||||
- 90 -
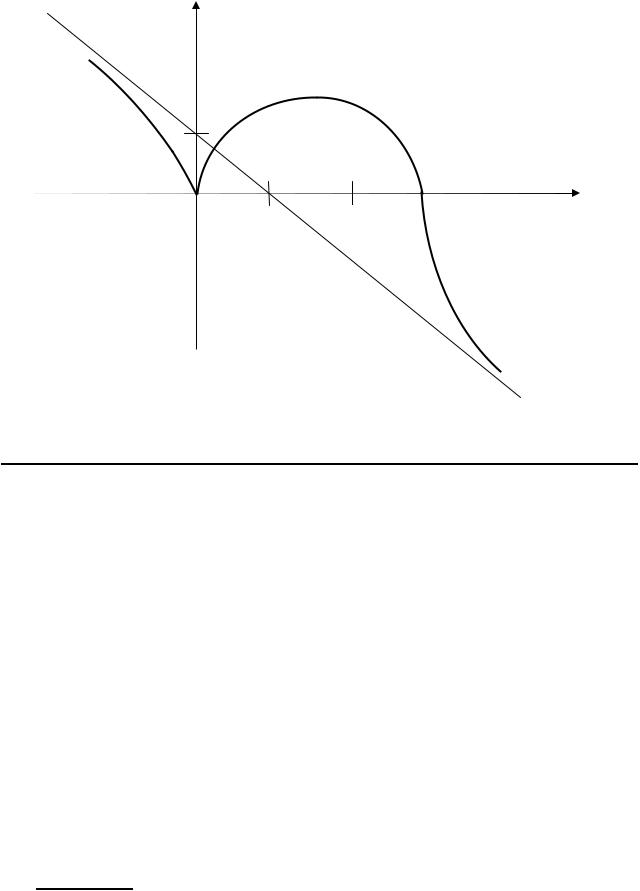
y
1
3 x
1 2
§7. Наибольшее и наименьшее значение функции на промежутке
Пусть функция y = f (x) непрерывна на замкнутом промежутке [a,b]. В
силу одного из свойств таких функций она достигает на этом промежутке своих наибольшего и наименьшего значений. Эти значения могут достигаться как внутри промежутка, так и на его концах. Если своего наибольшего (наименьшего) значения функция достигает во внутренней точке промежутка, то такая точка является точкой локального максимума (минимума), а значит и критической точкой первого порядка.
Можно предложить следующий алгоритм отыскания наибольшего и наименьшего значений.
1.Найти f '(x).
2.Найти критические точки первого порядка и отобрать из них те, которые лежат внутри промежутка [a,b].
3.Вычислить значения функции в точках, полученных в предыдущем пункте, а также на концах отрезка.
4.Из ряда чисел, полученных в предыдущем пункте, выбрать наибольшее и
наименьшее: |
они и |
являются |
соответственно наибольшим и наименьшим |
||||
значениями функции |
y = f (x) |
на промежутке |
[a,b]. |
||||
Пример |
|
1. |
Найдем наибольшее и |
наименьшее значения функции |
|||
f (x) = |
|
x |
|
на промежутке [-1,4]. |
|
||
|
|
|
|
||||
x2 |
+ 4 |
|
|||||
|
|
|
|
|
|||
- 91 -
