
МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть 1
.pdf
III |
Свойства б.б. последовательностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1. Пусть {bn } - б.б. Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
а) {bn } - неограниченна; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
б) {- bn и {bn |
|
|
|
|
- бесконечно большие; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
в) {Cbn },C ¹ 0 - бесконечно большая; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
г) если |
|
g n |
|
³ |
|
bn |
|
, то {g n } - бесконечно большая; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
д) если |
|
lim |
|
x |
|
n = |
|
a ¹ 0, то {xn × bn} - бесконечно большая; |
|
|
|
|
|
||||||||||||||||||||||||
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2. Произведение бесконечно больших последовательностей есть бесконечно |
|||||||||||||||||||||||||||||||||||||
большая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1. Сумма, разность и частное бесконечно больших может быть |
|||||||||||||||||||||||||||||||||||||
каким угодно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Любой многочлен от n |
есть б.б. |
|
Покажем это на конкретном |
||||||||||||||||||||||||||||||||||
примере: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn = 3n3 - 2n2 - 5n +1 = n3(3- 2× 1 - 5× |
1 |
|
+ |
|
1 |
) = |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
n2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
||
|
= n3(3- o(1) - o(1) + o(1)) = n3(3+ o(1)). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Так как {n3 - эталонная б.б., а lim(3+ o(1)) = 3 ¹ 0 , то {xn} - б.б. |
|
|
|
||||||||||||||||||||||||||||||||||
|
Замечание 2. Запишем ряд б.б., отношения которых является б.м.: |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ln n << na << an << n!<< nn |
|
|
(a > 0,a > 1) |
|
|
|
|
|
||||||||||||||||||||||||
|
Запись |
a << b |
|
|
|
означает, |
что |
a |
= o(1) . |
|
|
Докажем, |
например, |
что |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
= o(1) . Обозначим [a]= k и |
|
|
a |
|
= q < 1. Тогда для n > k |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n! |
k |
+1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 < xn = |
an = a |
|
× a |
|
×...× a × |
|
|
a |
× |
|
a |
×...× a |
< |
|
ak × |
a |
|
× |
a |
|
×...× |
|
a |
|
= |
||||||||||||
|
|
|
|
k |
+1 |
k |
+ 2 |
|
k +1 |
k +1 |
k |
+1 |
||||||||||||||||||||||||||
|
|
n! 1 2 |
|
|
k |
|
|
|
n |
|
k! |
|
|
|
||||||||||||||||||||||||
|
= ak qn-k = C × qn |
= o(1), т.к. 0 < q < 1. Следовательно, и xn = o(1) . |
|
|
||||||||||||||||||||||||||||||||||
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln n = o(1) и |
na = o(1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
na |
|
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
проведем позже, используя т.н. правило Бернулли-Лопиталя.
- 22 -
Лекция 4
§7. Теоремы о пределах последовательностей
Теорема 1. lim C = C . n®¥
Теорема 2 ( арифметические операции с пределами). Пусть последовательности {xn} и {yn } - сходящиеся. Тогда сходящимися будут и такие
последовательности: |
|
|
|
|
{Cxn}; {xn + yn}; {xn - yn}; |
|
|
{xn × yn}; {xn / yn}, |
|||||||||||||||||||||||||||||||
если только lim yn ¹ 0. При этом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1) |
|
lim Cxn = C lim xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
n®¥ |
|
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2) |
|
lim (xn Ä yn ) = ( lim xn ) Ä ( lim yn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
n®¥ |
|
|
|
|
|
|
|
|
n®¥ |
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(здесь Ä - символ любой арифметической операции). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
Ограничимся |
|
|
доказательством |
сходимости |
|
|
частного. |
|
|
Пусть |
|||||||||||||||||||||||||
|
xn = a +an , yn = b + bn , |
где |
an = o(1) |
и |
bn = o(1),b ¹ 0. |
Преобразуем |
|||||||||||||||||||||||||||||||||
частное следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
n |
|
|
a |
|
|
æ a +a |
n |
|
a |
ö |
|
|
a |
|
(a +a |
|
)b - a(b + b |
|
) |
|
a |
|
ba |
n |
- ab |
n |
|
1 |
|
||||||||
|
|
= |
|
|
+ ç |
|
|
- |
|
|
÷ |
= |
|
+ |
|
n |
|
|
|
|
n |
|
= |
|
|
+ |
|
|
|
× |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
yn |
|
|
b |
|
ç |
|
+ bn |
b |
÷ |
|
|
b |
|
b(b + bn ) |
|
|
|
b |
|
|
|
|
b |
|
|
yn |
|
|||||||||||
|
|
|
|
|
è b |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
В |
|
полученном выражении |
|
ban - abn = o(1), как |
линейная |
комбинация |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì 1 |
|
ü |
- ограничена, т.к. lim yn ¹ 0. Следовательно, |
|
|
|||||||||||||||||||||
бесконечно малых, а í |
|
|
|
ý |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
î yn þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
xn |
|
= a |
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
lim xn |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ o(1) . Это и доказывает: lim |
= |
n®¥ |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
n®¥ yn |
|
lim yn |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Теорема 3 (предельный переход в неравенствах). Пусть последовательности |
|||||||||||||||||||||||||||||||||||
{xn} и {yn } - сходящиеся. Тогда, если |
xn < yn |
(или |
xn £ yn ), |
то и |
|||||||||||||||||||||||||||||||||||
|
lim xn £ lim yn . В частности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
n®¥ |
|
|
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
а) если xn > 0 |
(xn < 0), то lim xn ³ 0 |
( lim xn £ 0) ; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n®¥ |
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
б) если xn > a |
|
(xn < a), то lim xn ³ a |
( lim xn £ a) . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n®¥ |
|
n®¥ |
|
|
|
lim xn = lim zn = a |
|||||||||||||
|
|
|
|
Теорема 4 (достаточное условие сходимости). Если |
|
|
|||||||||||||||||||||||||||||||||
и для всех n справедливо неравенство xn £ yn £ zn , |
|
|
|
|
n®¥ |
|
|
n®¥ |
|
|
|||||||||||||||||||||||||||||
то |
lim yn = a . |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n®¥ |
|
|
|
|
|
|
|
|||
- 23 -

Для доказательства воспользуемся определением предела на языке окрестностей. Рассмотрим произвольную e -окрестность числа b. Обозначим ее
O(e,b). Так |
как |
lim xn = b Þ $N1, "n ³ N1 : xn ÎO(e,b) , |
а |
так как |
||||||
|
|
|
|
n®¥ |
|
|
|
|
|
|
lim zn = b Þ $N2, |
"n ³ N2 : zn ÎO(e,b) . Тогда |
в |
силу |
неравенства |
||||||
n®¥ |
|
|
|
|
|
|
|
|
|
|
xn £ yn £ zn имеем: |
yn ÎO(e,b) "n ³ max(N1, N2 ) . Итак, для произвольной |
|||||||||
e -окрестности мы нашли номер |
N = max(N1, N2 ) , начиная с которого члены |
|||||||||
{yn } принадлежат этой окрестности. Это и означает, что lim yn = b. |
|
|
||||||||
|
|
|
|
|
|
|
n®¥ |
|
|
|
|
Пример. |
Рассмотрим |
последовательность |
с |
общим |
членом |
||||
zn = |
1 |
+ |
1 |
+ ... + |
1 |
. |
|
|
|
|
n2 |
n2 |
n2 |
|
|
|
|
||||
|
+1 |
+ 2 |
+ n |
|
|
|
|
|||
Чтобы оценить zn сверху, заменим каждое слагаемое наибольшим (это первое слагаемое), а чтобы оценить zn снизу, заменим слагаемые наименьшим (это последнее). Получим
n |
£ zn £ |
n |
или |
1 |
|
£ zn £ |
1 |
|
. |
|
n2 |
n2 |
1 |
1 |
|||||||
+ n |
+1 |
|
|
|||||||
|
|
|
|
1+ |
|
|
1+ |
|
|
|
|
|
|
|
n |
|
n2 |
|
|||
Подкоренные выражения обеих корней имеют вид 1+ o(1), следовательно,
сходятся к 1. Значит, lim |
1 |
|
= lim |
1 |
|
= |
1 |
= 1. |
n®¥ 1+ |
1 |
n®¥ 1+ |
1 |
|
1 |
|
||
n |
n2 |
|
|
|
||||
|
|
|
|
|
|
|
||
Отсюда вытекает, что lim zn = 1. n®¥
Замечание 1. При решении примера было использовано одно свойство элементарных функций, вытекающее из их непрерывности: если члены {xn} и её
lim xn = a принадлежат области определения элементарной функции n®¥
y = f (x) , то знак предела можно вносить под знак функции
lim f (xn ) = f (lim xn ) = f (a) . |
|
n®¥ |
n®¥ |
Замечание 2. Обратим внимание |
на следующее. Общий член zn |
представляет собой сумму n слагаемых, каждое из которых является бесконечно малой. Однако, здесь нельзя сказать, что сумма б.м. есть б.м., ибо число слагаемых неограниченно возрастает.
- 24 -

§8. Монотонные последовательности. Число e
I О пределе монотонной последовательности
Уже известно, что сходящаяся последовательность – ограничена. Однако, не всякая ограниченная последовательность имеет конечный предел: примером
может служить последовательность {(-1)n .
Одним из условий, обеспечивающих существование предела, является монотонность ограниченной последовательности.
Теорема. 1. Всякая ограниченная монотонная последовательность имеет конечный предел. 2. Всякая неограниченная монотонная последовательность является бесконечно большой (определенного знака).
Заметим, что для убывающей последовательности достаточно доказывать ограниченность снизу, а для возрастающей – ограниченность сверху.
Пример. Рассмотрим последовательность с общим членом xn = (n!)2 . Для
(2n)!
доказательства монотонности преобразуем член xn+1: |
|
|
|
|
|
|
||||||||||
xn+1 = |
((n +1)!)2 |
|
= |
|
(n!(n +1))2 |
= |
(n +1)2 |
|
|
× |
(n!)2 |
|
= |
|||
(2(n +1))! |
(2n)!(2n +1)(2n + 2) |
(2n +1)(2n |
+ 2) |
|
(2n)! |
|||||||||||
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
× xn . |
|
|
|
|
|
|
|
|
|
|
|
|
||
2(2n +1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Мы получили рекуррентное соотношение |
|
|
|
|
|
|
|
|
||||||||
xn+1 = yn × xn , где yn = |
n +1 |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
4n + 2 |
|
|
|
|
|
yn Î(0,1) , |
|||
Члены данной последовательности положительны, а |
|
|||||||||||||||
следовательно, xn+1 < xn , т.е. {xn} - убывает. Ее ограниченность |
снизу |
|||||||||||||||
очевидна, ибо xn > 0.
Сформулированная выше теорема обеспечивает существование конечного
предела lim xn = C . Для последовательности yn нетрудно получить: |
|||||||||
n®¥ |
|
|
|
|
|
|
|
|
|
yn = 1 |
+ |
0,5 |
= |
1 |
+ o(1), т.е. |
lim yn |
= |
1 . |
|
4n + 2 |
4 |
||||||||
4 |
|
|
|
n®¥ |
|
4 |
|||
Теперь перейдем к пределу в обеих частях рекуррентного соотношения, причем в правой части имеем право использовать теорему о пределе
произведения (ибо {xn} и {yn } - сходящиеся):
lim xn+1 = lim yn × lim xn или |
C = |
1 |
×C . |
|
n®¥ |
n®¥ n®¥ |
|
4 |
|
Отсюда получаем: C = lim xn = 0. n®¥
- 25 -

II Число е
Рассмотрим последовательность с общим членом
æ |
|
1 ön |
|
xn = ç1 |
+ |
|
÷ |
|
|||
è |
|
n ø |
|
и попытаемся применить к ней теорему, сформулированную выше.
Монотонный характер {xn} непосредственно не усматривается, так как с
|
æ |
+ |
1 ö |
|
возрастанием показателя степени n |
основание степени ç1 |
|
÷ убывает. Чтобы |
|
|
||||
|
è |
|
n ø |
|
убедиться в монотонности, разложим степень по формуле бинома Ньютона:
|
æ |
|
|
|
1 |
ön |
|
|
n |
n(n -1) ×...× (n - k +1) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
xn = |
ç1 |
+ |
|
|
÷ |
= å |
|
|
|
|
|
|
× |
|
= |
|
|
|
|
|
|
|
|
|
||||||||
n |
|
|
k! |
|
|
nk |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
è |
|
|
|
ø |
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
1 |
|
|
n |
|
|
n -1 |
|
|
n - 2 |
|
n - k +1 |
n 1 |
æ |
|
|
1 ö æ |
|
2 ö |
æ |
|
k -1ö |
||||||||||
= å |
|
|
× |
|
|
× |
|
|
|
|
× |
|
|
|
×...× |
|
|
= å |
|
|
×ç1 |
- |
|
÷ ×ç1 |
- |
|
÷ |
×...×ç1 |
- |
|
÷. |
|
|
|
n |
|
|
n |
|
|
|
n |
n |
|
|
|
|
|
|||||||||||||||||
k =0k! |
|
|
|
|
|
|
|
|
|
k =0k! |
è |
|
|
n ø è |
|
n ø |
è |
|
n ø |
|||||||||||||
Если теперь от xn перейти к xn+1, т.е. увеличить n на единицу, то, вопервых, добавится еще одно (положительное) слагаемое, а, во-вторых, каждое из
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
l |
ö |
|
|
|
||
уже написанных слагаемых увеличится, ибо множители вида ç1- |
|
|
÷ заменятся |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
n ø |
|
|
|
|||
|
|
|
|
æ |
|
|
|
l |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
большими множителями ç1- |
|
|
|
÷. Отсюда следует, что xn+1 > xn , |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
è |
|
|
n +1ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т.е. последовательность {xn} - возрастающая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В последнем выражении для xn |
опустим все скобки. |
Тем самым каждое |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
||
слагаемое увеличится и мы получим оценку: xn < å |
|
|
= 2 + |
|
|
+ |
|
|
|
+ ... + |
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Учитывая, что k!> 2k -1 |
|
|
|
|
|
|
|
k =0 k! |
|
2! |
|
3! |
|
n! |
|
|||||||||||||
|
"k ³ 2, усилим эту оценку: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
1 |
|
|
|
|
1 |
|
|
æ |
|
1 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn < 2 + |
|
+ |
|
|
+ ... |
+ |
|
|
|
= 2 + |
ç1- |
|
|
÷ < 3. |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
2 |
2 |
2 |
n-1 |
2 |
n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(Здесь использована формула для суммы геометрической прогрессии). Итак, последовательность {xn} возрастает и ограничена сверху, следовательно, она имеет конечный предел. Его обозначают буквой e . Это число
|
æ |
|
1 ön |
||
e = lim |
ç1 |
+ |
|
÷ |
= 2,71828... |
|
|||||
n®¥è |
|
n ø |
|
||
имеет исключительную важность, как для самого математического анализа, так и для его приложений.
- 26 -

Лекция 5
§9. Предел функции
I Общее определение
Договоримся о терминологии. Термин «число b» означает как обычное число, так и один из символов: + ¥ или - ¥ . Термин «точка a » означает как конченую точку, так и «бесконечно удаленную»: + ¥ , - ¥ или ¥ . При этом под
окрестностью такой |
«бесконечно удаленной» точки |
понимается интервал |
(A,+¥), (-¥,- A) |
или объединение этих интервалов |
соответственно (при |
произвольном A > 0).
Окрестностью же конечной точки понимаем любой интервал, содержащий эту точку. Для простоты формулировок и для бесконечно больших последовательностей будем говорить: «последовательность сходится (к + ¥, - ¥ или ¥ )».
Рассмотрим функцию f (x), определенную в некоторой окрестности точки
a (за исключением, быть может, самой точки a ) и возьмем из этой окрестности последовательность точек
x1, x2 ,..., xn ,..., |
(1) |
отличных от a и сходящуюся к a . Значения |
функции в точках этой |
последовательности также образуют числовую последовательность |
|
f (x1), f (x2 ),..., f (xn ),..., |
(2) |
и можно ставить вопрос существования ее предела. |
|
Определение 1 (язык последовательностей). Число b называют пределом функции f (x) в точке x = a (или при x ® a ) и пишут
b = lim f (x) (или: f (x) ® b при x ® a ), x®a
если для любой сходящейся к a последовательности (1) значений аргумента x , отличных от a , соответствующая последовательность (2) значений функции сходится к числу b.
Геометрический смысл |
равенства b = lim f (x): |
график |
функции в |
||||
|
|
|
x®a |
|
|
|
|
окрестности точки x = a приближается (стремится) к точке (a,b) . |
|
|
|||||
Пример 1. |
Вычислим |
предел |
f (x) = x2 в |
точке |
x = 3. |
Рассмотрим |
|
произвольную |
последовательность |
{xn}: xn ¹ 3 |
и |
lim xn = 3. |
Для |
||
|
|
|
|
|
n®¥ |
|
|
соответствующей последовательности значений функции {f (xn )}= {xn2 |
имеем |
||||||
lim |
f (xn ) = lim xn2 = lim xn × lim xn = 3×3 = 9. Таким образом, lim x2 = 9. |
||||
n®¥ |
n®¥ n®¥ |
|
|
x®3 |
|
|
Пример 2. |
Покажем, что предел функции |
f (x) = sin |
1 |
при x ® 0 не |
|
|
|
|
x |
|
существует. Рассмотрим две последовательности значений аргумента с членами
- 27 -

xn = |
1 |
|
и zn = |
1 |
|
. Очевидно, что lim xn = lim zn = 0. При этом для |
||||
2pn |
|
p |
||||||||
|
|
2pn + |
|
|
|
n®¥ |
n®¥ |
|||
|
|
|
|
2 |
|
|
|
|
|
|
последовательностей значений функции: |
|
|||||||||
|
lim |
f (xn ) = lim sin(2pn) = lim 0 = 0, |
|
|||||||
|
n®¥ |
|
n®¥ |
|
|
n®¥ |
|
|||
|
lim |
|
æ |
|
|
p |
ö |
= lim 1 = 1. |
|
|
|
f (zn ) = lim çsin 2pn + |
2 |
÷ |
|
||||||
|
n®¥ |
|
n®¥è |
|
|
ø |
n®¥ |
|
||
Таким образом, для двух сходящихся к 0 последовательностей значений аргумента соответствующие последовательности значений функций имеют разные пределы. А это по определению предела функции и означает, что
lim f (x) не существует. x®0
II Частные случаи. Важные понятия
А) Предел на бесконечности (a = ±¥ ).
Определение 2.
|
|
|
b = lim f (x) Û "{xn |
}( lim xn |
= +¥) Þ ( lim |
f (xn ) = b). |
|
|||||
|
|
|
x®+¥ |
n®¥ |
|
n®¥ |
|
|
|
|
||
|
|
|
Аналогичное определение и для x ® -¥. |
|
|
|
|
|||||
|
|
|
Пример 3. f (x) = |
sin x |
, a = +¥ . Рассмотрим "{xn}: lim xn = +¥. Тогда |
|||||||
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
1 |
|
ü |
|
для последовательности значений функции {f (xn )}= í |
|
×sin xn ý будем иметь: |
||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
î xn |
|
þ |
|
|
|
1 |
= o(1) , т.к. {xn } - б.б., а {sin xn } - ограничена, значит |
f (xn ) = o(1) , т.е. |
|||||||||
|
|
|||||||||||
|
xn |
|
|
|
|
|
|
|
|
|
|
|
lim f (xn ) = 0. Это означает, что |
lim |
sin x |
= 0. |
|
|
|
|
|||||
|
|
|
|
|
|
x®+¥ |
x |
|
|
|
|
|
|
|
|
Нетрудно убедиться, что и |
lim |
sin x |
= 0. Для тех функций, для которых |
||||||
|
|
|
|
|
|
x®-¥ |
x |
|
|
|
|
|
|
lim |
f (x) = lim f (x) = b, |
можно писать lim f (x) = b . |
Напротив, писать |
||||||||
|
x®+¥ |
x®-¥ |
|
|
|
x®¥ |
|
|
|
|
||
|
lim arctg x нельзя, ибо lim |
arctg x = p , а |
lim arctg x = - p . |
|
||||||||
|
x®¥ |
x®+¥ |
|
2 |
x®-¥ |
|
|
2 |
|
|||
|
|
|
Геометрическая иллюстрация: конечный предел функции на |
+ ¥(-¥) |
||||||||
означает наличие у графика функции |
горизонтальной асимптоты на |
+ ¥ (на |
||||||||||
- ¥ ). |
|
|
|
|
|
|
|
|
|
|
||
- 28 -

В) Бесконечно малые функции (b = 0).
Определение 3. Функцию y = f (x) называют бесконечно малой (б.м.) в точке x = a (или: при x ® a ) и пишут « f (x) = o(1) при x ® a », если
lim f (x) = 0, т .е.
x®a
"{xn}( lim xn = a, xn ¹ a) Þ ( f (xn ) = o(1) ïðè n ® ¥) .
n®¥
Например, в предыдущем пункте мы показали, что sinx x = o(1) при
x ® ¥.
Основной результат дает следующая теорема.
Теорема 1. Функция f (x) имеет в точке x = a предел lim f (x) = b тогда x®a
и только тогда, когда разность f (x) - b есть б.м. при x ® a :
b = lim f (x) Û f (x) = b + o(1) при x ® a . |
|
|
|
|
|||||
x®a |
|
|
|
|
|
|
|
|
|
С) Бесконечно большие функции (b = ±¥). |
|
|
|
|
|||||
Определение 4. Функцию |
f (x) называют бесконечно большой (б.б.) в |
||||||||
точке x = a (при x ® a ), если lim f (x) = +¥ или - ¥ , т.е. |
|
|
|||||||
|
x®a |
|
|
|
|
|
|
||
"{xn}( lim xn = a, xn ¹ a) Þ {f (xn )} |
- б.б. последовательность опреде- |
||||||||
n®¥ |
|
|
|
|
|
|
|
||
ленного знака. |
|
|
|
|
|
|
|
|
|
Все свойства б.м. и б.б. последовательностей остаются справедливыми и |
|||||||||
для б.м. и б.б. функций. Приведем лишь некоторые из них. |
|
|
|
|
|||||
Теорема 2. |
Для того, чтобы функция |
f (x) была бесконечно большой в |
|||||||
точке x = a необходимо и достаточно, чтобы функция |
|
1 |
была бесконечно |
||||||
|
|
|
|||||||
|
f (x) |
||||||||
|
|
|
|
|
|
|
|||
малой в этой же точке. |
|
|
|
|
|
|
|
||
И два свойства. |
|
|
|
|
|
|
|
||
1) Если a(x) = o(1) при |
x ® a , а |
f (x) - ограничена в |
некоторой |
||||||
окрестности точки x = a , то произведение a(x)× f (x) = o(1) при x ® a . |
|||||||||
2) Если b (x) - б.б. в точке x = a , а |
f (x) такова, |
что |
lim f (x) = b ¹ 0, |
||||||
|
b (x)× f (x) есть б.б. функция при x ® a . |
x®a |
|
||||||
то произведение |
|
|
|||||||
Например, |
f (x) = x ×sin |
1 = o(1) |
в точке |
x = 0, а |
многочлен |
||||
|
|
x |
|
|
|
|
|
|
|
g(x) = x2 - 7x -1 есть б.б. на ± ¥ , ибо g(x) = x2 (1- 7 |
- |
1 |
) = x2 (1+ o(1)). |
||||||
x2 |
|||||||||
|
|
|
x |
|
|
|
|||
- 29 -
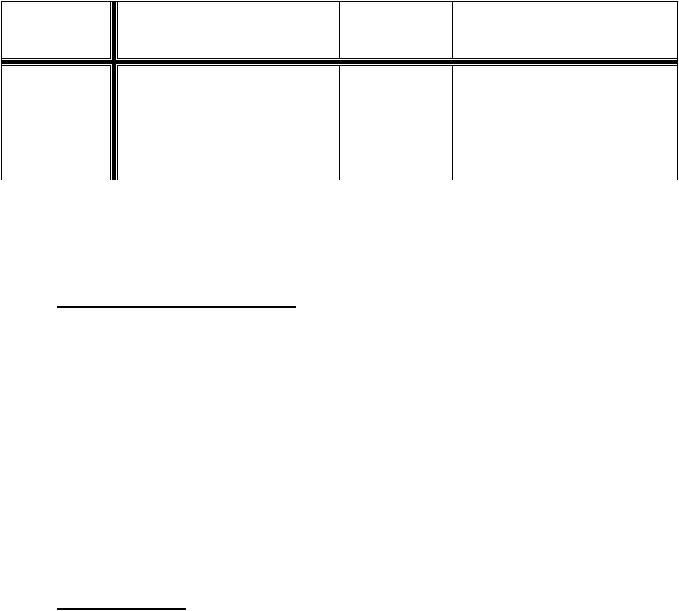
Эталонные б.б. и б.м. функции приведем в таблице.
|
xa ,a > 0 |
1 |
,a > 0 |
a x ,a > 1 |
a x ,0 < a < 1 |
ln x |
|
|
|
xa |
|||||
|
|
|
|
|
|
|
|
б.м |
x ® 0 |
|
x ® +¥ |
x ® -¥ |
x ® +¥ |
x ® 1 |
|
б.б. |
x ® +¥ |
|
x ® 0 |
x ® +¥ |
x ® -¥ |
x ® +¥ , |
|
|
x ® 0 |
||||||
|
|
|
|
|
|
|
|
Так же как и б.б. последовательности, б.б. функции можно упорядочить по |
|||||||
их порядку роста: при x ® +¥ |
|
|
|
|
|||
ln x << xa << ax |
(a > 0, a > 1) . |
|
|
|
|||
III |
Односторонние пределы |
|
|
|
|||
Рассмотрим функцию |
f (x) = sign x. |
Для произвольной б.м. |
|||||
последовательности {xn} положительных чисел рассмотрим последовательность
{(-1)n × xn . Как произведение ограниченной на б.м., она сходится к нулю.
Соответствующая |
последовательность |
значений |
функции |
|
{f (xn )}= {sign((-1)n × xn )}= {sign(-1)n }= {(-1)n |
не имеет предела. Это |
|||
означает, что limsign x |
не существует. Однако, |
"{xn}, xn = o(1) |
и xn > 0 |
|
x®0 |
|
|
|
|
имеем lim sign xn =1, а для "{yn }, yn = o(1) и yn < 0 |
- limsign yn = -1. |
|||
n®¥ |
|
|
n®¥ |
|
|
|
|
|
|
Такая ситуация характерна для многих функций, |
у которых нет предела в |
|||
какой-либо точке, что и привело к появлению понятия односторонних пределов.
Определение 5. Пусть
"{xn},( lim xn = a, xn > a) Þ lim |
f (xn ) = b . |
|
|
||||
|
n®¥ |
n®¥ |
|
|
|
|
|
Тогда число b называют правым пределом (пределом справа или |
|||||||
правосторонним |
пределом) функции |
f (x) в |
точке |
x = a и |
пишут: |
||
b = lim |
f (x) или b = f (a + 0). |
|
|
|
|
||
x®a+0 |
|
|
|
|
|
|
xn > a |
Определение левого предела аналогично, только |
требование |
||||||
заменяют требованием |
xn < 0. Обозначения: |
|
|
|
|||
b = |
lim |
f (x) или b = f (a - 0) . |
|
|
|
|
|
x®a-0 |
|
|
|
|
|
|
|
Если |
a = 0, то |
иногда вместо |
f (0 ± 0) |
пишут |
f (±0). Например, |
||
sign(+0) = 1, sign(-0) = -1.
- 30 -

Сформулируем теорему, на которой базируется использование
односторонних пределов. |
|
|
|
предела lim f (x) = b |
|
|
|
|||||
Теорема 3. |
Для существования |
необходимо и |
||||||||||
|
|
|
|
|
|
|
x®a |
|
|
|
|
|
достаточно существования |
порознь |
и |
равенство |
односторонних пределов: |
||||||||
f (a + 0) = f (a - 0) = b . |
|
|
|
|
|
|
|
|
|
|
|
|
IV Теоремы о пределах функций |
|
|
|
|
|
|
|
|
||||
Теорема 4. Пусть у функции f (x) |
существует |
lim f (x) = b > 0. Тогда в |
||||||||||
|
|
|
|
|
|
|
|
x®a |
|
|
|
|
некоторой окрестности точки |
x = a (за исключением, быть может, |
самой точки |
||||||||||
x = a ) f (x) > 0 . |
Более того, "B Î(0, A) f (x) ³ B > 0. |
|
|
|
|
|||||||
Теорема 5. |
Пусть у |
функции |
f (x) |
существует конечный |
предел при |
|||||||
x ® a . Тогда в некоторой окрестности точки |
x = a функция |
f (x) |
ограничена. |
|||||||||
Теорема 6. |
Функция |
|
f (x) = C = const |
имеет предел |
в |
каждой |
точке |
|||||
числовой прямой, причем lim |
f (x) = C . |
|
|
|
|
|
|
|
|
|||
|
x®a |
|
|
|
|
|
|
|
|
|
|
|
Теорема 7 |
(операции над пределами). |
Пусть функции |
f (x) и |
g(x) |
||||||||
имеют в точке x = a конечные пределы b и d соответственно. Тогда в этой точке
имеют конечные |
пределы и |
функции: 1) |
C × f (x); |
2) f (x) + g(x); |
3) f (x) - g(x); 4) |
f (x)× g(x) ; |
5) f (x) / g(x) |
(при d ¹ 0). |
При этом имеют |
место следующие равенства:
lim Cf (x) = C ×b,
x®a
lim ( f (x) Ä g(x)) = b Ä d (здесь Ä - символ арифметической операции). x®a
Для доказательства рассмотрим {xn}(xn ¹ a) - произвольную последовательность значений аргумента, сходящуюся к x = a .
В силу существования пределов функций f (x) и g(x) соответствующие последовательности значений функций {f (xn )} и {g(xn )} имеют пределы b и d . Тогда, используя теорему 2 §7, получим, что последовательность
{f (xn ) Ä g(xn ) сходится к b Ä d . Согласно определению предела функции это |
|||||
означает, что lim ( f (x) Ä g(x)) = b Ä d . |
|
|
|
||
|
x®a |
|
|
|
|
|
Теорема 8 (предельный переход в неравенствах). Пусть функции |
f (x) |
и |
||
g(x) |
имеют в точке x = a |
конечные пределы и в некоторой окрестности этой |
|||
точки |
(за исключением, быть может, самой |
точки) f (x) ³ g(x) . Тогда |
и |
||
lim f (x) ³ lim g(x) . В |
частности, если |
f (x) ³ 0 ( f (x) £ 0 ), |
то |
и |
|
x®a |
x®a |
|
|
|
|
lim f (x) ³ 0 ( lim f (x) £ 0). |
|
|
|
||
x®a |
x®a |
|
|
|
|
|
|
- 31 - |
|
|
|
