n |
|
|
|
n |
|
|
|
|
n |
|
n |
n |
å(xk - |
|
)2 = å(xk2 - 2 |
|
|
|
|
|
|
|
|
|
|
x |
xxk + (x)2 ) = åxk2 - 2xåxk + å(x)2 = |
k =1 |
|
|
|
k =1 |
|
|
|
k =1 |
|
k =1 |
k =1 |
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
= åxk2 - 2 |
|
× n × |
|
+ n( |
|
)2 = åxk2 - n( |
|
)2. |
|
|
|
|
|
x |
x |
x |
x |
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
Но сумма квадратов, стоящая в начале этой цепочки равенств, строго положительна (ибо не все xk одинаковые), следовательно, и
n
å xk2 - n(x)2 > 0.
k =1
Из этого неравенства легко получить требуемое нам:
n |
æ |
n |
ö |
2 |
nåxk2 |
- çç |
åxk ÷÷ |
> 0. |
k =1 |
è k =1 |
ø |
|
Замечание. Полученное неравенство есть частный случай неравенства КошиБуняковского
(åakbk )2 £ åak 2 × åbk 2 ,
которое является обобщением неравенства для векторов: (a ×b)2 £ a 2 × b 2 .
III Исследование системы нормальных уравнений |
|
Вернёмся к системе (2). Её определитель: |
|
|
|
|
|
|
|
D = |
|
åxk2 |
åx |
|
= n |
å |
x2 |
- ( |
x |
k |
)2 |
> 0, |
|
|
|
|
åx |
n |
|
|
k |
å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. D ¹ 0, следовательно система (2) имеет единственное решение, а функция (1) одну стационарную точку M0 (a0 ,b0 ). Чтобы исследовать эту точку, найдём значения вторых производных функции (1) в этой точке:
|
|
n |
|
|
|
|
S¢¢ |
= 2 |
å |
x2 |
, |
S¢¢ |
= 2n, |
aa |
|
k |
|
bb |
|
k=1
Определитель, составленный из этих чисел
|
D = |
|
2åxk2 |
2åx |
|
= 4(n |
|
xk2 |
- ( |
|
xk )2 )> 0, |
|
|
|
|
|
|
|
|
|
2åx |
2n |
|
|
å |
|
å |
|
|
|
|
|
|
|
|
|
|
|
|
значит в точке |
M |
0 |
|
есть экстремум, а так как |
S¢¢ |
> 0, то этот экстремум – |
|
|
|
|
|
|
|
|
|
aa |
|
|
минимум.
- 132 -
Итак, задача минимизации функции S(a,b) всегда имеет единственное решение.
Пример. Результаты измерений приведены в таблице:
x |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
y |
3 |
2 |
2 |
1 |
2 |
1 |
0 |
Используя метод наименьших квадратов, определить “наилучшие” значения параметров линейной функции y = ax + b .
Решение. Вычислим коэффициенты системы нормальных уравнений (2):
7 |
7 |
7 |
7 |
åxk = 14, |
å yk = 11, |
åxk2 = 56, |
åxk yk = 11. |
k =1 |
k =1 |
k =1 |
k =1 |
Составим систему: |
|
|
|
ì56a +14b = 11, íî14a + 7b = 11.
Её решение: a = - 1128 , b = 1433. Линейная функция, которая “наилучшим”
образом описывает результаты измерений, имеет вид:
y = - 1128 x + 1433.
z = x - iy
z = x + iy
Тема Комплексные числа и многочлены
Лекция 22
|
|
|
|
|
§1. |
Комплексные числа: основные определения |
Символ i |
вводят соотношением |
i2 = -1 и называют мнимой единицей. |
Другими словами, i = |
-1. |
z = x + i × y , где xÎ R, y Î R , называется |
Определение. Выражение вида |
комплексным числом, |
при этом число x называют |
вещественной частью |
комплексного числа z |
и обозначают x = Re z , число y |
– мнимой частью z и |
обозначают y = Im z .
Из такого определения следует, что действительные числа – это те комплексные числа, мнимая часть которых равна нулю.
Комплексные числа удобно изображать точками плоскости, на которой задана декартова прямоугольная система координат, а именно: комплексному числу соответствует точка M (x, y) и наоборот. На оси Ox изображаются вещественные числа и её называют вещественной осью. Комплексные числа вида z = iy (Re z = 0) называют чисто мнимыми. Они изображаются точками на оси Oy , которую называют мнимой осью. Эту
плоскость, служащую для изображения комплексных чисел, называют комплексной плоскостью. Комплексное число, не являющееся действительным, т.е. такое, что Im z ¹ 0, иногда называют мнимым.
Два комплексных числа называют равными тогда и только тогда, когда у них совпадают как вещественные, так и мнимые части.
Сложение, вычитание и умножение комплексных чисел производится по
обычным |
правилам алгебры многочленов с учётом того, что |
i2 = -1, i3 |
= -i , i4 =1,... . Операцию деления можно определить как обратную к |
операции умножения и доказать единственность результата (если делитель отличен от нуля). Однако на практике используется другой подход.
Комплексные числа z = x + iy и называют сопряжёнными, на
комплексной плоскости они изображаются точками, симметричными относительно вещественной оси. Очевидно, что:
1)z º R Û z = z ;
2)z + z = 2xÎ R ;
3)z × z = x2 + y2 Î R .
Теперь разделить z1 |
на z2 |
можно следующим образом: |
|
z1 |
= |
z1 × |
|
|
|
= |
|
1 |
|
|
|
|
|
|
|
z2 |
|
|
×(x + iy ) ×(x |
|
- iy |
|
) . |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
z |
|
× z |
|
|
|
|
x2 |
+ y2 |
1 |
1 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
Не трудно показать, что
- 134 -
z1 Ä z2 = (z1 Ä z2 ) ,
где символ Ä обозначает любую арифметическую операцию.
Пусть z = a + bi некоторое мнимое число, а x – вещественная переменная. Произведение двух биномов
(x - z)(x - z) = (x - a - bi)(x - a + bi) = (x - a)2 - (bi)2 = x2 - 2ax + a2 + b2
есть квадратный трёхчлен с действительными коэффициентами.
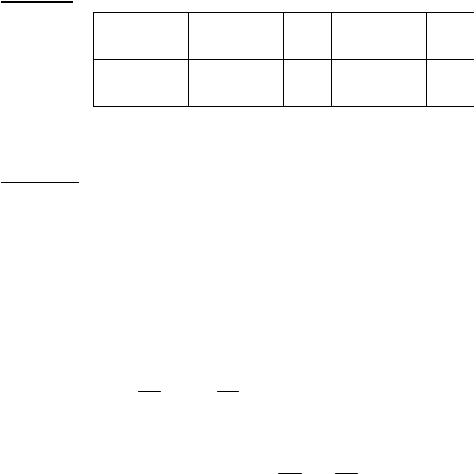
Теперь, имея в распоряжении комплексные числа, мы сможем решить любое квадратное уравнение ax2 + bx + c = 0. Если D = b2 - 4ac < 0, то
 D = - D =
D = - D =  -1× D = i ×
-1× D = i ×  - D
- D
и уравнение имеет два комплексных сопряжённых корня
x |
= - b |
± i × - D . |
1,2 |
2a |
2a |
|
Если D > 0, то |
уравнение имеет два различных вещественных корня. Если |
D = 0, то уравнение имеет два одинаковых корня.
§2. Тригонометрическая форма комплексного числа
Как говорилось выше, комплексное число z = x + i y удобно изображать точкой M (x, y). Можно также такое число отождествлять с радиус-вектором
этой точки OM = {x, y}. При такой интерпретации сложение и вычитание
комплексных чисел производится по правилам сложения и вычитания векторов. Для умножения и деления комплексных чисел более удобной оказывается другая форма.
Введём на комплексной плоскости Oxy полярную систему координат. Тогда M (x, y) = M (r,j), где x = r cosj , y = r sinj и комплексное число z = x + i y можно записать в виде:
z = r(cosj + i sinj).
Эту форму записи называют тригонометрической (в отличие от алгебраической формы z = x + i y ). В этой форме число r называют модулем, а
j – аргументом комплексного числа z . Они обозначаются: r = z , j = Arg z . Для модуля имеем формулу
z = x2 + y2 =  z × z
z × z
Аргумент числа определён неоднозначно, а с точностью до слагаемого 2p n, n º Z . Значение аргумента, удовлетворяющего неравенствам -p < j £ p ,
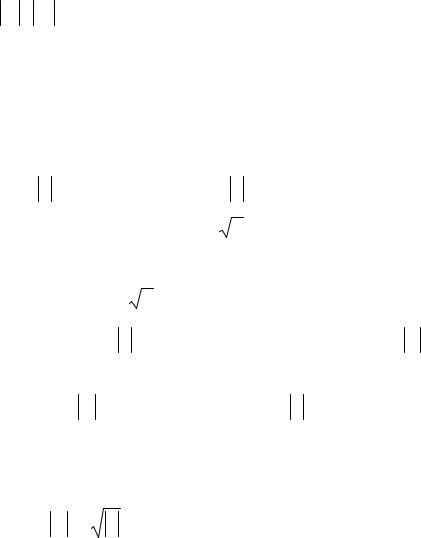
называется главным и обозначается arg z . Тогда Argz = arg z + 2p n , nÎ N . Для главного значения аргумента можно получить такие выражения:
- 135 -
ì |
|
|
|
arctg |
y |
, x > 0, |
|
ï |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
ï |
|
y |
|
|
|
|
|
|
|
|
ïarctg |
+ π sign y, x < 0, y ¹ 0, |
|
|
, |
arg z = í |
px |
|
|
ï |
|
|
|
ï |
2 |
sign y, x = 0, y ¹ 0, |
|
ï |
|
p , x < 0, y = 0, |
|
|
|
|
|
î |
|
|
|
|
аргумент числа z = 0 считается неопределённым.
Условие равенства двух комплексных чисел в тригонометрической форме имеет вид: модули чисел равны, а аргументы отличаются на число кратное 2p .
Найдём произведение двух комплексных чисел в тригонометрической форме:
z1 × z2 = ρ1(cosj1 + i sinj1) × ρ2 (cosj2 + i sinj2 ) =
=ρ1 × ρ2 ((cosj1 ×cosj2 - sinj1 ×sinj2 ) + i (sinj1 ×cosj2 + cosj1 ×sinj2 ) =
=z1 × z2 (cos(j1 +j2 ) + i sin(j1 +j2 )).
Итак, при умножении чисел их модули умножаются, а аргументы складываются.
Аналогичным образом можно установить, что при делении модули чисел делятся, а аргументы вычитаются.
Понимая возведение в степень как многократное умножение, можно получить формулу возведения комплексного числа в степень:
(z ×(cosj + i sinj))n = z n × (cosj + i sinj),"n ÎZ .
Выведем формулу для n z – корня n -ой степени из комплексного числа z (не путать с арифметическим корнем из действительного числа!). Операция извлечения корня является обратной по отношению к операции возведения в
степень. Поэтому n z – это комплексное число z такое, что z n = z .
Пусть z = z (cosj + i sinj) известно, а z = z (cosy + i siny ) требуется найти. Тогда
z n = z n (cosny + i sin ny ) = z (cosj + i sinj) .
Из равенства двух комплексных чисел в тригонометрической форме следует, что
|
|
z |
|
n = |
|
z |
|
, |
ny = j + 2p k , k ÎZ . |
|
|
|
|
Отсюда z |
= n z (это арифметический корень!), |

y = j + 2p k , k ÎZ . n
Нетрудно убедиться, что y может принимать лишь n различных по существу
значений, например, при |
k = 0,1,2,..., n -1. Окончательно имеем формулу: |
n z (cosj + i sinj) = n |
z (cosj + 2p k |
+ i sin j + 2p k ), k = 0,1,2,..., n -1. |
|
n |
n |
Итак, корень n -ой степени из комплексного числа имеет n различных значений. На комплексной плоскости эти значения располагаются в вершинах
правильно n -угольника, вписанного в окружность радиуса n z с центром в начале координат. “Первый” корень имеет аргумент j n, аргументы двух “соседних” корней отличаются на 2p
n, аргументы двух “соседних” корней отличаются на 2p n.
n.
Пример. Извлечём корень кубический из мнимой единицы: z = i , z =1, arg z = p 2. Тогда:
2. Тогда:
|
z = 3 i |
|
= 3 1(cosp 2 + i sinp 2) = 3 1æcos p 2 + 2p k + i sin p 2 + 2p k ö |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
3 |
3 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
k = 0,1,2; |
|
|
|
z1 |
= cos p |
|
+ i sin p = |
3 + |
1 |
×i , |
|
|
|
|
|
|
6 |
|
|
6 |
2 |
2 |
|
|
|
|
|
|
|
|
z 2 |
= cos(p |
+ |
2p ) + i sin(p |
+ |
|
2p ) = - |
3 |
+ 1 |
×i , |
|
|
|
|
6 |
|
3 |
|
6 |
|
3 |
|
2 |
2 |
|
|
|
z3 |
= cos(p |
+ |
4p |
) + i sin(p |
+ |
|
4p |
) = -i . |
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
§3. Показательная форма комплексного числа
Вспомним второй замечательный предел
|
|
|
|
|
|
|
|
æ |
|
|
|
1 |
ön |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ç1+ |
|
÷ |
= e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n®¥è |
|
|
|
n ø |
|
|
|
|
|
|
|
|
|
|
Отсюда нетрудно получить, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
x ö |
n |
æ |
æ |
|
x |
|
n |
öx |
|
æ |
æ |
|
|
|
n |
öx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
ö x ÷ |
|
ç |
|
x ö x ÷ |
|
x |
|
lim ç1 |
+ |
|
÷ |
|
= ç lim |
ç1 |
+ |
|
|
÷ |
÷ |
= |
ç lim |
ç1 |
+ |
|
÷ |
÷ |
= e |
|
, |
|
|
n |
|
|
n®¥è |
|
n ø |
|
çn®¥è |
|
ø |
÷ |
|
çn®¥è |
|
n ø |
÷ |
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
è |
|
|
|
|
ø |
|
|
|
т.е. показательную функцию ex действительного аргумента можно определить как некоторый предел. Естественно попробовать определить показательную функцию мнимого аргумента таким же образом:
|
iy |
= |
|
æ |
+ |
iy ön |
y Î R , i = -1. |
e |
|
lim |
ç1 |
|
÷ |
, |
|
|
|
|
|
n®¥è |
|
n ø |
|
|
Сначала «разберёмся» со степенью, стоящей под знаком предела:
|
|
y |
|
æ y ö |
2 |
y |
|
|
если z =1+ i |
|
, z = |
1+ ç ÷ |
, arg z = arctg |
|
, то |
|
n |
n |
|
|
|
è n ø |
|
|
zn = z n (cos(n × arg z) + i sin(n × arg z)).
Найдём отдельно пределы модуля и аргумента числа zn :
|
|
|
æ |
æ y ö2 |
ö |
n |
|
æ |
|
|
|
|
|
|
|
n |
2 |
¥ |
|
|
lim |
z |
|
= lim ç1 |
+ ç |
|
÷ |
÷ |
|
= [1 |
] = expç lim |
|
|
|
|
|
è |
è n ø |
ø |
|
|
è |
n®¥ |
|
n®¥ç |
|
|
|
÷ |
|
|
çn®¥ |
æ |
n |
|
y |
2 |
ö |
|
0 |
|
ç |
× |
|
÷ |
= e |
=1, |
|
|
2 |
|
= expç lim |
2 |
n |
÷ |
|
èn®¥ |
|
|
ø |
|
|
|
|
n |
|
æ |
y ö |
|
æ |
y ö |
lim arg(z |
|
) = lim |
çn ×arctg |
|
÷ |
= lim |
çn × |
|
÷ |
|
|
|
n®¥ |
|
n®¥è |
n ø |
n®¥è |
n ø |
n |
æ |
æ y ö2 |
öö |
|
|
lnç1 |
+ ç |
|
÷ |
÷÷ |
= |
|
|
2 |
ç |
è n ø |
÷÷ |
|
è |
øø |
|
= y .
|
æ |
|
iy ön |
Итак, lim |
ç1 |
+ |
|
÷ |
= 1× cos y + i sin y и мы приходим к известной формуле |
|
n®¥è |
|
n ø |
|
Эйлера:
eij = cosj +
Отсюда легко получить
z = z (cosj + i sinj):
z = z ei arg z .
Из формул (*) и (**) вещественного аргумента:
i sinj . |
(*) |
показательную |
форму комплексного числа |
(**)
получим выражения для косинуса и синуса
|
cosj = |
eij + e-ij |
, |
sinj = |
eij - e-ij |
. |
|
2 |
2i |
|
|
|
|
|
Используя показательную форму, можно рассмотреть комплексно-значную функцию комплексного переменного:
- 138 -
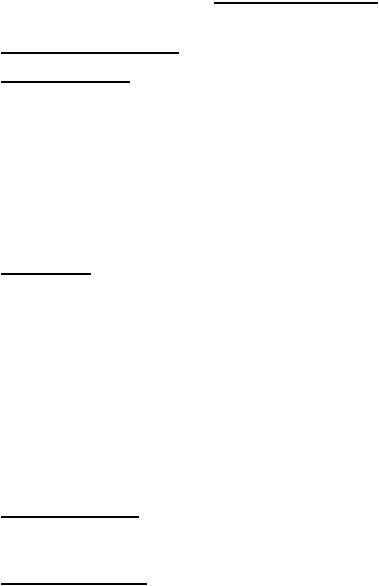
w = ez = ex+iy = ex (cos y + i sin y) = ex cos y + iex sin y .
Лекция 23
§4. Многочлены
I Общие результаты
Определение 1. Многочленом n -ой степени называют функцию вида
Pn (x) = a0 xn + a1xn-1 + ... + an-1x + an ,
где x – переменная (вообще говоря, комплексная), a0 , a1,..., an – некоторые постоянные числа (вообще говоря, комплексные), причём a0 ¹ 0.
Известно, что многочлены можно делить «столбиком» и справедлива теорема.
Теорема 1. Каковы бы ни были многочлены Pn (x) и Tm (x), m £ n, найдутся многочлены Qn-m (x) и Rk (x) , причем k < m, такие, что имеет место равенство:
Pn (x) = Tm (x) × Qn-m (x) + Rk (x) .
По отношению к четырём многочленам из этой теоремы применяют обычные термины: делимое, делитель, частное, остаток.
Говорят, что Pn (x) делится на Tm (x), если остаток Rk (x) = 0.
Многочленом нулевой степени естественно называть любое постоянное число (вещественное или комплексное).
Определение 2. Число x0 называют корнем многочлена Pn (x), если
Pn (x0 ) = 0.
Теорема 2 (Безу). Остаток от деления Pn (x) на бином (x - a) есть значение многочлена в точке a .
Действительно, т.к. делитель (x - a) имеет первую степень, то остаток должен быть нулевой степени:
Pn (x) = (x - a) ×Qn-1(x) + R0
Тогда Pn (0) = 0 + R0 , что и требовалось доказать.
Из этой теоремы вытекает важное следствие (которое часто называют теоремой Безу).
Следствие. Число x0 является корнем многочлена Pn (x) тогда и только тогда, когда Pn (x) делится на (x - x0 ) , т.е.
Pn (x) = (x - x0 ) ×Qn-1(x)
Заметим, что старший коэффициент частного Qn-1(x) совпадает со старшим коэффициентом делимого Pn (x).
Ответ на вопрос о наличии корней у многочлена даёт основная теорема алгебры, которую принимаем без доказательства.
Теорема 3. Всякий многочлен ненулевой степени имеет, по крайней мере, один корень (вещественный или комплексный).
Из этой теоремы можно получить ряд следствий.
1. |
Всякий многочлен Pn (x), n ³1 можно разложить на |
n линейных |
множителей |
|
|
Pn (x) = a0 (x - x1) × (x - x2 ) ×...× (x - xn ) . |
(1) |
2. |
Многочлен степени n имеет не более чем n различных корней. |
Из разложения (1) следует, что числа x1, x2 ,..., xn – корни многочлена Pn (x)
идругих чисел, обращающих многочлен в нуль, нет.
3.В разложении (1) множители могут повторяться; если через x1, x2 ,..., xm обозначить различные корни многочлена Pn (x) получим:
|
|
P (x) = a |
0 |
(x - x )x1 |
× (x - x |
2 |
)x2 ×...× (x - x |
n |
)xn , |
|
(2) |
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь kl |
называют кратностью корня xl и |
k1 + k2 + ... + km = n . |
Можно дать |
такое определение кратности корня: число |
x0 |
называют k -кратным корнем |
многочлена Pn (x), если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (x) = (x - x |
0 |
)k |
× Q |
(x) |
и |
Q |
(x |
0 |
) ¹ 0. |
|
|
|
|
n |
|
|
|
|
n-k |
|
|
|
|
n-k |
|
|
|
|
|
|
|
|
4. Всякий многочлен степени n ( n ³1) имеет ровно n корней, если каждый |
из корней считать столько раз, какова его кратность. |
|
|
|
|
|
|
|
|
|
II Многочлены с действиьтельными коэффициентами |
|
|
Пусть |
комплексное |
число |
z |
|
|
|
является |
|
|
|
корнем |
многочлена |
P (z) = a zn + a zn-1 + ... + a |
n |
|
с |
действительными |
|
коэффициентами, |
т.е. |
n |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn (z) = 0 |
|
ak = |
|
|
k = 0,1,2,..., n. |
|
|
|
|
и |
ak |
, |
Рассмотрим число |
z |
и вспомним, |
что |
операция “сопряжения” перестановочна с любой арифметической операцией. Тогда:
- 140 -

Pn (z) = a0 (z)n + a1(z)n-1 +...+ an = a0 zn + a1 zn-1 +...+ an = = (a0 zn ) + (a1zn-1) +...+ an = (a0 zn + a1zn-1 +...+ an ) = 0 = 0.
Итак, справедлива теорема.
Теорема 4. Если комплексное число z = a + b ×i является корнем многочлена
с действительными коэффициентами, то и сопряжённое ему число z = a - b ×i является корнем этого многочлена (причём, с той же кратностью).
Из этой теоремы можно получить ряд следствий.
1.У многочлена с действительными коэффициентами число комплексных корней – чётно.
2.Многочлен нечётной степени (с действительными коэффициентами) имеет, по крайней мере, один действительный корень.
3.В разложении (2) перемножим скобки, соответствующие комплексным сопряжённым корням:
(x - z)k (x - z)k = ((x - a - bi)(x - a + bi))k = x2 + p x + q ,
где p = -2a, q = a2 + b2 . Таким образом, получим основной результат:
всякий многочлен с действительными коэффициентами можно разложить в
произведение множителей двух типов: линейных – |
(x - a )ki |
и квадратичных – |
|
|
|
|
i |
|
|
|
|
|
(x2 + p x + q )li , где |
a , p ,q |
– действительные числа, причём |
p2 |
- 4q |
i |
< 0. |
i |
i |
i i i |
|
|
|
i |
|
|
Линейные множители соответствуют действительным корням, квадратичные – парам комплексных сопряжённых.
Список рекомендованной литературы
1.Ильин В.А., Позняк Э.К. Основы математического анализа, ч. I. – М.: «Наука», 1982. – с. 616.
2.Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: «Наука», 1966. – с. 544.
3.Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты).
–М.: «Высш. школа», 1983. – с. 175.
4.Методические указания и задания к расчетно-графической работе по разделу курса высшей математики «Пределы, непрерывность, производная» (для
студентов направления подготовки 6.050102 «Программная инженерия»)/ Составитель: Скворцов А.Е.– Донецк: ДонНТУ, 2008. – с. 48




 D = - D =
D = - D =  -1× D = i ×
-1× D = i ×  - D
- D z × z
z × z