МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть 1

IV Точка разрыва 2го рода

Точка x0 называется точкой разрыва 2го рода функции y=f(x), если в этой

точке, хотя бы один из односторонних пределов функции равен ±¥ или не существует.

7) См. пример 2 §9.

Замечание 1. При исследовании функции на непрерывность необходимо различать элементарные и неэлементарные функции. Например,

разрыва. Их тип устанавливается путем вычисления односторонних пределов. Функция же

не является, вообще говоря, элементарной, поэтому может иметь разрыв в любой точке. Но каждое из трех выражений, определяющих функцию, есть элементарное, а значит, непрерывно. Эта функция может иметь разрывы только в точках, в которых переходит с одного выражения на другое. Итак, точки

возможного разрыва x1 = 0, x2 =1.

Замечание 2. Монотонная ограниченная функция может иметь разрывы только 1го рода (следствие теоремы 12 §9).

- 43 -

§14. Основные свойства непрерывных функций

1.Устойчивость знака. Если функция f(x) непрерывна в точке x0 и f(x0)≠0, то в некоторой окрестности точки x0 функция f(x) сохраняет знак.

2.Локальная ограниченность. Если функция f(x) непрерывна в точке x0, то она ограничена в некоторой окрестности точки x0.

3.Ограниченность на промежутке (1я теорема Вейерштрасса). Если

функция f(x) непрерывна на замкнутом промежутке [a,b], то она ограничена на

этом промежутке.

4. Достижение наибольшего и наименьшего значений (2я теорема Вейерштрасса). Если функция f(x) непрерывна на замкнутом промежутке [a,b],

то она достигает своих наибольшего и наименьшего значений, т.е.

$ x1, x2 Î[a,b], "x Î[a,b]:

5. Прохождение через ноль (1я теорема Больцано-Коши). Пусть функция f(x) непрерывна на промежутке [a,b] и на его концах имеет значения разных знаков. Тогда $c Î (a,b): f (c) = 0 . Если же f(x) еще и строго монотонная, то

f (1) = 1 – значения разных знаков. Значит, $c Î(0,1): f (c) = 0 . Это число c и

есть корень уравнения x3 + x -1 = 0.

На этом свойстве основан метод интервалов решения неравенств: непрерывная функция между своими нулями сохраняет знак.

6. Прохождение через промежуточные значения (2я теорема Больцано-

Коши). Пусть функция f(x) непрерывна на промежутке [a,b], причем

f (a) = A, f (b) = B . Тогда

"C Î(A, B)$c Î(a,b) : f (c) = C .

Другими словами, непрерывная функция, переходя от одного значения к другому, принимает и все промежуточные значения.

7. Существование обратной функции. Непрерывная строго монотонная функция имеет обратную также непрерывную строго монотонную с тем же направлением монотонности.

- 44 -

Тема ПРОИЗВОДНАЯ

Лекция 8

§1. Задачи, приводящие к понятию производной

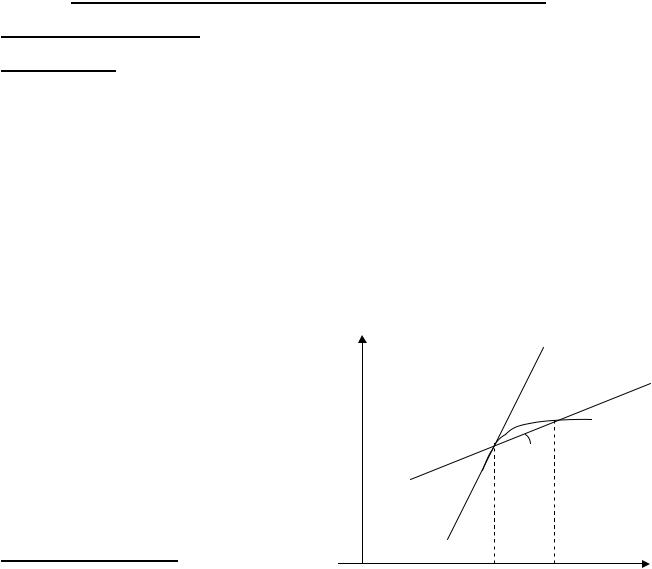
I Задача о касательной

Определение. Касательной к линии L в ее точке М0 называется предельное положение секущей M0M, когда точка M вдоль линии L стремится произвольным образом к совпадению с точкой M0.

Чтобы придать математическую строгость этому определению, будем считать, что линия L – это график некоторой функции y = f (x).

Пусть M0 (x0 , f (x0 )) – фиксированная точка графика, а M (x, f (x)) – текущая точка. Обозначим Dx = x - x0 , Df = f (x) - f (x0 ). Стремление точки M к М0 равносильно x ® x0 или Dx ® 0 . Через точку М0 проходит много прямых, все они отличаются друг от друга угловыми коэффициентами. Касательная к графику в точке М0 – это та прямая, угловой коэффициент которой есть предел углового коэффициента

секущей M0M при x ® x0 :

координата точки на прямой в момент времени t ). Важной характеристикой движения является скорость. Для равномерного движения (т.е. движения с

скорость постоянная, полученный ответ не будет зависеть ни от t0 , ни от Dt .

- 45 -

Используя 2) легко написать уравнение касательной:

y= f (x0 ) + f ¢(x0 ) × (x - x0 )

инормали, т.е. прямой, проходящей через точку касания перпендикулярно

касательной:

Из общих теорем о пределах можно получить такую теорему. - 47 -

Теорема 1. Функция f (x) имеет в точке x0 производную тогда и только

тогда, когда она имеет в этой точке равные друг другу односторонние производные.

Пример 2. Для функции f (x) = e x найти правую и левую производную в

нуле.

совпадающие правая и левая касательные в точке (x0 , f (x0 )) . Такая точка графика называется угловой. Если же производная (хотя бы односторонняя) равна

- ¥ , то это означает, что у графика имеется вертикальная касательная.

§4. Дифференцируемость функции

Определение. Говорят, что функция y = f (x) дифференцируема в точке x0, если ее приращение Dy = f (x0 + Dx) - f (x0 ) можно представить в виде

Dy = A× Dx + o(Dx), Dx ® 0, (1)

- 48 -

где A – некоторое число, не зависящее от Dx .

Теорема 1. Для того, чтобы функция y = f (x), была дифференцируемой в

точке x0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Dy = f ¢(x0 )Dx + o(1) × Dx .

В этом соотношении нетрудно увидеть равенство (1). Теорема доказана. Таким образом, для функции одной переменной дифференцируемость и

существование конечной производной – понятия равносильные. Формулу

Dy = f ¢(x0 ) × Dx + o(Dx)

называют формулой бесконечно малых приращений.

Между понятиями дифференцируемости и непрерывности существует связь, устанавливаемая следующей теоремой.

Теорема 2. Если функция y = f (x) дифференцируема в точке x0, то она и

из определений непрерывности.

Естественно возникает вопрос о том, справедливо ли утверждение, обратное теореме 2, т.е. “непрерывная функция дифференцируема”. На этот вопрос следует дать отрицательный ответ: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в данной точке. Примером может служить

функция из примера 2 §3: y = e x . Она непрерывна в нуле, но y¢(0) не

существует.

Приведем еще один пример такой функции.

- 49 -

Данная функция – неэлементарная, возможная точка разрыва x = 0 (в этой точке одно элементарное выражение меняется на другое). Но

следовательно, f (x) непрерывна в точке x = 0. Найдем производную функции в

Но нам уже известно, что, когда аргумент синуса стремится в ¥, синус предела не имеет. Итак, f ¢(0) не существует, т.е. f (x) недифференцируема в нуле.

Отметим, что математиками построены примеры функций, непрерывных на некотором промежутке, но не имеющих производной ни в одной точке этого промежутка.

Лекция 9

§5. Основные правила дифференцирования

(Cu)¢ = C ×u¢ (постоянный множитель можно вынести за знак производной). III–V. Если функции u = u(x) и v = v(x) дифференцируемы в точке x, то

их сумма, разность, произведение и частное (если v(x) ¹ 0) также

дифференцируемы в этой точке, причем имеют место формулы:

III. (u ± v)¢ = u¢ ± v¢;

IV. (u ×v)¢ = u¢×v + u ×v¢;

Докажем, например, формулу дифференцирования частного. Пусть y = uv .

- 50 -