симума, ни минимума, ибо z(0,0) = 0, а в любой окрестности этой точки функ-
ция принимает как положительные, так и отрицательные значения.
Чтобы сформулировать достаточное условие экстремума функции двух пе-
ременных введем специальные обозначения. Пусть |
M0 (x0 , y0 ) |
– стационарная |
точка функции |
z(x, y) и пусть в ее окрестности существуют непрерывные част- |
ные производные второго порядка. Обозначим z¢¢ |
(M |
0 |
) = a , |
z¢¢ (M |
0 |
) = a |
22 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
11 |
yy |
|
|
z¢¢ |
= a |
|
, z¢¢ |
= a |
21 |
(напомним, что a |
= a |
21 |
) и |
|
|
|
|
|
|
|
|
|
xy |
12 |
|
yx |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
2 |
= |
|
a11 |
a12 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2 (достаточное условие экстремума). |
|
|
|
|
|
|
|
|
|
|
1. |
Функция z= z(x, y) имеет в своей стационарной точке |
M0 экстремум, |
если D2 |
> 0, |
причем |
M0 – точка минимума, если |
|
a11 > 0 , и точка максимума, |
если a11 < 0.
2. |
Если D2 < 0, то в точке M0 нет экстремума. |
3. |
Случай D2 = 0 требует дополнительного исследования. |
Рассмотрим теперь случай функции n переменных z = z(x1, x2 ,..., xn ). Пусть точка M0 (xi ) – стационарная точка, т.е z¢xi (M 0 ) = 0 "i. Предположим,
что в некоторой окрестности этой точки существуют непрерывные частные производные второго порядка. Обозначим
aij = z¢x¢i x j (M0 ), i, j = 1,2,…,n.
Из этих чисел составим матрицу A = (aij ). Определители, составленные из эле-
ментов первых |
k строк и |
k столбцов, |
|
|
называются главными минорами данной |
матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
= a , |
D |
|
= |
|
a11 |
a12 |
|
, D |
|
= |
|
a11 |
a21 |
a13 |
|
,...,D |
|
= det A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
3 |
|
a |
21 |
a |
22 |
a |
23 |
|
n |
|
|
11 |
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 3. 1) Если все главные миноры положительны, то функция имеет в |
точке M0 |
локальный минимум. |
2) |
Если знаки миноров чередуются, причем |
D1 < 0, то M0 |
– точка локального максимума. |
|
|
|
|
|
|
|
Пример 1. Исследовать на экстремум функцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
z = x3 + y3 - 3xy. |
|
|
|
|
|
|
Решение. Находим частные производные первого порядка: z¢ = 3x 2 - 3y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
z¢ = 3y 2 |
- 3x. Находим стационарные точки: |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

ì |
z¢ |
= 0, |
ì |
2 |
- y = 0, |
ì |
|
|
2 |
, |
ì |
3 |
-1) |
= 0, |
x |
|
ïx |
|
ïy = x |
|
ïx(x |
|
í |
z¢y = 0, |
Û í |
|
|
Û í |
|
|
|
|
Û í |
|
|
|
|
|
î |
ï |
2 |
- x = 0, |
ï |
4 |
- x |
= 0, |
ï |
|
|
2 |
. |
|
|
|
îy |
|
îx |
|
îy = x |
|
|
Имеем две стационарные точки M1(0,0) и M2 (1,1). Чтобы исследовать эти точки, вычисляем производные второго порядка:
|
z¢¢ |
= 6x, z¢¢ |
= 6y, z¢¢ |
|
= z¢¢ |
|
= -3. |
|
|
xx |
|
|
yy |
|
|
|
xy |
yx |
|
Составим из этих производных определитель: |
|
|
|
D |
2 |
(M ) = |
|
6x - 3 |
|
= 36xy - 9. |
|
|
|
|
|
|
|
|
|
- 3 |
6y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В точке M1 : D2 (M1) = D2 (0,0) = -9 < 0, следовательно, в точке M1 нет экстре- |
мума. В точке |
M2 :D2 (M2 ) = D2 (1,1) = 36 - 9 > 0, следовательно, в точке M2 |
функция имеет экстремум; так как |
z¢¢ (M |
2 |
) > 0, то этот экстремум – минимум. |
|
|
|
|
|
|
|
|
xx |
|
|
|
|
Пример 2. Исследовать на экстремум функцию трех переменных |
|
u = x3 + y2 + z2 +12xy - 2z +1. |
Решение. |
u¢ = 3x2 |
+12y, u¢ = 2y +12x, u¢ = 2z - 2 и |
|
x |
|
|
|
|
|
|
y |
|
|
|
|
z |
|
ìu¢x = 0, |
ìx2 + 4y = 0, |
ìy = -6x , |
|
ïu¢ |
= 0, Û ïy + 6x = 0, Û |
ïx2 - 24x = 0, |
|
í y |
|
|
|
í |
|
|
|
|
|
|
í |
|
|
ï |
= 0, |
ï |
|
|
|
|
|
|
ï |
|
|
îu¢z |
îz -1 = 0, |
|
|
|
îz = 1. |
Имеем две стационарные точки: M1(0,0,1) и M2 (24,-144,1). Далее:
|
|
u¢¢ |
= 6x, |
|
|
u¢¢ |
= 2, |
u¢¢ |
= 2, |
|
|
|
|
|
|
|
|
|
xx |
|
|
|
yy |
|
|
zz |
|
|
|
|
|
|
|
|
|
|
u¢¢ |
= u¢¢ |
= 12, |
u¢¢ = u¢¢ |
= 0, u¢¢ |
= u¢¢ |
= 0. |
|
|
|
|
xy |
yx |
|
|
|
|
xz |
zx |
|
|
|
yz |
zy |
|
|
|
Вычислим эти производные в точке |
M2 |
и составим матрицу |
|
|
|
|
|
|
|
|
|
|
|
|
æ144 |
12 |
0 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
12 |
2 |
0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = ç |
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 |
0 |
2 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
|
|
Найдем главные миноры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
=144 > 0, D |
2 |
= |
|
144 12 |
|
= 144× 2 -122 |
> 0, D |
3 |
= det A = D |
2 |
× 2 > 0 |
|
|
1 |
|
|
|
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все главные миноры положительные, значит M2 (24,-144,1) – точка минимума. В точке M1(0,0,1) матрица вторых проиводных имеет вид
z¢x , z¢y ,
z(x, y)
|
|
|
æ |
0 |
2 |
0 |
ö |
|
|
A = |
ç |
2 |
2 |
0 |
÷ |
|
|
ç |
÷ |
|
|
|
ç |
0 |
0 |
2 |
÷ |
|
|
|
è |
ø |
Минор D1 = 0. Это означает, что требуется дополнительное исследование. В точ- |
ке M1 |
функция равна u(0,0,1) = 0. В то же время, при изменении аргументов |
функции вдоль прямой |
|
|
|
|
|
ìy = 0 |
функция имеет вид |
|
u |p = x3 |
и в сколь угодно малой окрестности |
p : í |
|
|
îz = 1 |
|
|
|
|
|
|
точки M1 принимает как положительные, так и отрицательные значения. Следовательно, в этой точке нет экстремума.
§12. Наибольшее и наименьшее значения функции в области
Известно, что, если функция непрерывна в ограниченной замкнутой области, то она достигает своего наибольшего и наименьшего значения. Если, кроме того, функция имеет внутри области частные производные то эти
значения она достигает либо внутри облати в стационарных точках, либо на границе области.
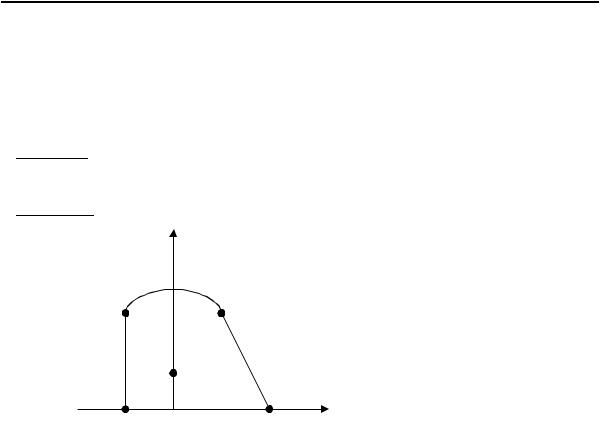
Пример. Найти наибольшее и наименьшее значение функции z = xy - x в
области D , ограниченной линиями: y = 0, y = 4 - x2 , x = -1 (x ³ -1). |
|
Решение. 1) находим стационарные точки внутри области D : |
|
|
|
у |
|
|
|
|
М5 |
|
М7 |
|
|
|
|
М1 |
|
|
|
|
|
0 |
|
х |
|
|
М2 |
М3 |
|
|
|
|
|
|
z¢x = y -1, z¢y = x. |
|
|
|
ìy -1 = 0, |
– стационарная точка M1(0,1). |
|
í |
|
|
îx = 0 |
|
|
|
|
2) Рассмотрим функцию на границе области.

2.1) z(x, y) |y =0 = -x = f1(x), -1 £ x £ 2. Это линейная функция, свои наибольшее и наименьшее значение достигает на концах промежутка: x = -1 и x = 2. Имеем еще две точки подлежащие исследованию: M2 (-1,0) и M3(2,0).
2.2) |
z(x, y) |x=-1= -y +1 = g(y), |
0 £ y £ 3. Эта функция также линейная, |
поэтому имеем еще две точки: M4 (-1,0) º M2 и M5 (-1,3). |
2.3) |
z(x, y) | |
y=4- x |
2 = 3x - x2 = f |
2 |
(x), -1£ x £ 2. Эта функция одной пе- |
|
|
|
|
ременной достигает наибольшего и наименьшего значения либо внутри проме-
жутка [-1,2] в точке, где |
f2¢(x) = 0, либо на концах промежутка. Производная |
f ¢(x) = 3 - 3x2 |
обращается в ноль в точках |
x = -1, x |
2 |
=1. |
Итак, имеем еще точ- |
2 |
|
|
1 |
|
|
ки: M6 (-1,3) º M5 , M7 (1,3) и M8 (2,0) º M3 .
3) Вычисляем значения функции в найденных “подозрительных” точках и выбираем из полученного ряда чисел наибольшее и наименьшее:
z(M1) = z(0,1) = 0, z(M2 ) = z(-1,0) = 1, z(M3 ) = z(2,0) = -2, z(M5 ) = z(-1,3) = -2, z(M7 ) = z(1,3) = 2,
max z(x, y) = z(1,3) = 2,
D
min z(x, y) = z(2,0) = z(-1,3) = -2.
D
Лекция 21
§13. Производная по направлению. Градиент
I Производная по направлению
В одномерном случае производная функции f (x) характеризует скорость изменения функции в данной точке в направлении оси Ox . В двумерном случае частные производные функции z(x, y) характеризуют то же самое в направлении координатных осей.
Естественно поставить вопрос о скорости изменения |
функции z(x, y) в |
направлении произвольной оси |
l . |
|
Пусть |
функция z(x, y) |
определена в некоторой |
окрестности точки |
M0 (x0 , y0 ) |
и пусть ось l задана углами a и b , которые она составляет с осями |
координат. Ось удобно задавать её ортом: e = {cosa,cos b}. Будем считать, что
ось проходит через точку M0 |
и пусть точка M – произвольная точка, лежащая |
|
|
|
|
= t × |
|
. |
на оси. Тогда |
M0M |
|| |
e |
, т.е. |
M0M |
e |

Определение 1. Пусть точка |
M неограниченно приближается к точке M0 |
вдоль оси |
l . Предел вида |
|
|
|
|
|
|
|
|
|
|
lim |
z(M ) - z(M0 ) |
= lim |
z(x, y) - z(x0 , y0 ) |
(1) |
|
|
|
|
|
|
M ®M 0 |
t |
|
|
t ®0 |
t |
|
|
называется |
производной функции z(x, y) по направлению оси |
l в точке M0 и |
обозначается одним из символов |
|
|
|
|
|
|
|
|
|
|
|
¶z(M0 ) , |
¶z(x0 , y0 ) , |
¶z |
|
|
. |
|
|
|
|
|
|
|
¶l |
|
|
¶l |
¶l |
|
M |
0 |
|
|
|
|
|
|
|
Теорема 1. Пусть функция |
z(x, y) имеет в некоторой окрестности точки |
M0 (x0 , y0 ) непрерывные частные производные первого порядка и пусть ось l
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
образует с осями координат углы |
a и b . |
Тогда производная данной функции по |
направлению оси l в точке |
M0 |
существует и выражается формулой |
|
|
|
|
¶z |
|
|
= z¢x (M0 )cosa + z¢y (M0 )cos b . |
|
|
(2) |
|
|
|
|
|
¶l |
|
M |
|
|
|
|
|
0 |
|
M (x, y) |
|
|
оси l . |
|
|
|
|
|
|
|
|
|
Доказательство. Пусть |
– текущая |
точка |
Так |
как |
|
|
= {x - x0 , y - y0}, |
|
t × |
|
= {t cosa, t cos b} |
|
|
|
|
|
M0M |
а |
e |
и в |
силу |
того, |
что |
|
= t × |
|
, будем иметь: |
|
|
M0M |
e |
|
|
|
|
|
ì x - x0 = t cosa, |
ìx = x0 + t cosa, |
í |
í |
+ t cos b. |
|
|
|
îy - y0 = t cos b, |
îy = y0 |
То есть, координаты текущей точки M (x, y) есть функции параметра t . Тогда:
z(M ) = z(x, y) = z(x0 + t cosa, y0 + t cos b ) = F(t), z(M0 ) = F(0)
и из (1) имеем:
|
|
|
|
|
|
|
|
|
|
|
|
¶z |
|
|
= lim |
z(M ) - z(M0 ) |
= lim |
F(t) - F(0) |
. |
(3) |
|
¶l |
|
M0 |
|
|
|
t ®0 |
t |
|
t |
®0 |
|
t |
|
|
|
|
|
F(t) |
|
Последний предел есть производная |
функции |
в нуле. Производная |
же |
сложной функции F(t) существует, ибо z(x, y) имеет непрерывные производные, а её аргументы x = x0 + t cosa и y = y0 + t cos b – дифференцируемы, при этом:
F¢(t) = z¢x (x, y) × xt¢ + z¢y (x, y) × yt¢ = z¢x cosa + z¢y cos b .
Рассмотрим последнее равенство при t = 0 и получим
F¢(0) = z¢x (M0 )cosa + z¢y (M0 )cos b .
Теперь формула (3) и доказывает теорему. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. В случае функции трёх переменных U (x, y, z) и оси l , имеющей |
орт |
|
= {cosa,cosb,cosg} формула (2) приобретает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u |
|
|
= u¢x (M0 )cosa + u¢y (M0 )cos b + u¢z (M0 )cosg . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶l |
|
M |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вычислить производную функции z = 2x3 + xy2 в точке M0 (1,-2) |
по направлению вектора |
M0M1 |
, где M1(4,2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Найдём единичный вектор, имеющий данное направление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì3 |
|
4 |
ü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
M |
|
M |
|
|
|
|
|
|
|
|
M0M1 = {3,4}, |
|
|
0M1 = |
|
+ 4 |
= 5, |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
M |
3 |
|
|
e = |
|
|
|
|
|
|
|
|
|
= í |
|
, |
|
ý, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
M0M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î5 |
|
þ |
откуда cosa = 3 5, |
cos b = 4 5. Далее, вычислим частные производные данной |
функции в точке |
M |
0 |
: |
|
z¢ (x, y) = 6x2 |
+ y2 , |
|
z¢ |
(x, y) = 2xy , |
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
z¢ |
(M |
0 |
) = 6 ×12 + (-2)2 = 10, |
z¢ |
(M |
0 |
) = 6 ×1(-2) = -4. Теперь по формуле (2) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим
¶¶zl =10× 53 + (-4) × 54 = 145 .
II Градиент
Определение 2. Вектор, проекциями которого служат частные производные функции z(x, y) , называется градиентом функции
grad z = {z¢x (x, y), z¢y (x, y)}.
Для функции трёх переменных U (x, y, z) :
gradU = {Ux¢ ,U¢y ,Uz¢}.
Связь градиента с производной по направлению даётся следующей теоремой.
Теорема 2. Производная функции по направлению есть проекция её градиента на это направление:
¶¶zl = npl grad z .
Доказательство. Проекция вектора на ось – это проекция вектора на орт оси. Проекцию же вектора на вектор можно найти, используя скалярное произведение:
- 127 -
|
|
|
|
|
|
|
|
|
|
z = |
|
|
× |
|
|
|
z |
. |
|
|
|
|
|
|
|
np |
|
z = np |
|
|
e |
grad |
grad |
|
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
e |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
={cosa,cosb} и |
|
z = {z¢x , z¢y}, причём |
|
|
|
|
= 1, получим: |
Учитывая, что |
e |
grad |
|
e |
|
|
|
|
npl grad z = cosa × z¢x + cos b × z¢y .
Правая часть этого равенства в силу Теоремы 1 есть производная по направлению. Теорема доказана.
Следствие 1. Производная функции z(x, y) в точке M0 по направлению оси
l достигает максимума, когда это направление совпадает с градиентом функции, причём
max ¶z = grad z .
l ¶l
Таким образом, градиент функции в данной точке характеризует направление и величину максимальной скорости возрастания функции в данной точке.
Следствие 2. Производная функции по направлению, перпендикулярному её градиенту, равна нулю.
III Линии и поверхности уровня
Очень часто, чтобы яснее представить себе график функции z = z(x, y) (т.е. некоторую поверхность) используют т.н. линии уровня.
Определение 2. Линией уровня функции z(x, y) называют линию (в области определения z(x, y) ), вдоль которой функция принимает постоянное значение, т.е. линию, уравнение которой имеет вид z(x, y) = C , где C – константа.
Например, для функции z = x2 - y2 , линии уровня – это два семейства
(C > 0 и C < 0) сопряжённых гипербол, а так же биссектрисы координатных углов (C = 0).
Для функции трёх переменных U (x, y, z) аналогично вводится понятие поверхности уровня, т.е. поверхности, определяемой уравнением
U (x, y, z) = C .
Следствие 3. Градиент функции в заданной точке перпендикулярен линии (поверхности) уровня функции, проходящей через эту точку, т.е. направлен по нормали к линии (поверхности) уровня.
Доказательство. (Для функции двух переменных). Рассмотрим уравнение линии уровня функции z = z(x, y):
z(x, y) = C .
- 128 -
и её производная имеет
Это уравнение определяет неявную функцию y = y(x)
вид: y¢x = - z¢x  z¢y . Уравнение нормали к графику y = y(x) в точке M0 (x0 , y0 ):
z¢y . Уравнение нормали к графику y = y(x) в точке M0 (x0 , y0 ):
|
y - y0 |
= - |
|
|
1 |
|
× (x - x0 ) . |
|
|
|
|
|
|
|
y¢x (x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В нашем случае: |
y - y |
|
= - |
zy (x0, y0 ) |
× (x - x ) . Это уравнение легко |
0 |
|
|
|
|
|
|
|
|
zx (x0 |
, y0 ) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
переписать в канонической форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x - x0 |
= |
y - y0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z¢x |
|
z¢y |
|
|
|
|
|
|
|
|
что направляющий вектор нормали |
|
= {z¢x , z¢y} = |
|
z . |
Из которой следует, |
a |
grad |
Это и означает, что градиент функции направлен по нормали к линии уровня этой функции.
Пример. Для функции z =1- (0.5x2 + y2 ) линии уровня : z = C – это семейство эллипсов
|
|
|
x2 |
|
+ |
|
|
y2 |
|
= 1. |
|
|
2(1- C) |
1- C |
|
|
|
|
|
Проверим, что семейство парабол |
y = Cx2 |
|
пересекает все эти эллипсы под |
прямым углом. Дифференцируем уравнение эллипсов по x : |
|
|
2x |
|
+ |
|
2yy¢x |
|
= 0 |
|
2(1- C) |
1- C |
|
|
|
|
Отсюда угловой коэффициент касательной к эллипсу (в произвольной точке):
y¢ = - 2xy = k1 .
Для параболы тот же коэффициент имеет вид:
k2 = (Cx2 )¢ = 2Cx .
Пусть (x0 , y0 ) – точка пересечения какого-либо эллипса с некоторой параболой.
Тогда y0 = Cx02 и произведение угловых коэффициентов касательных в этой точке:
|
|
|
x |
|
|
|
Cx2 |
k × k |
2 |
= - |
0 |
× 2Cx |
0 |
= - |
0 |
= -1. |
|
|
1 |
|
2y0 |
|
|
y0 |
|
|
|
|
|
|
Отсюда следует, что касательные перпендикулярны, т.е. рассмотренные семейства взаимно-перпендикулярны. Градиент функции z =1- (0.5x2 + y2 ) в точке M0 (x0 , y0 ) направлен по касательной к той параболе из семейства y = Cx2 , которая проходит через M0, причём в сторону вершины параболы, ибо начало координат – это абсолютный максимум данной функции.
Одна интерпретация полученного результата. Поверхность, определяемая рассмотренной функции, – это эллиптический параболоид с вершиной в точке A(0,0,1), расположенный ниже плоскости z =1. Потоки воды с такой
поверхности стекают по траекториям, проекциями которых служат параболы семейства y = Cx2 .
§14. Метод наименьших квадратов
I Постановка задачи и суть метода
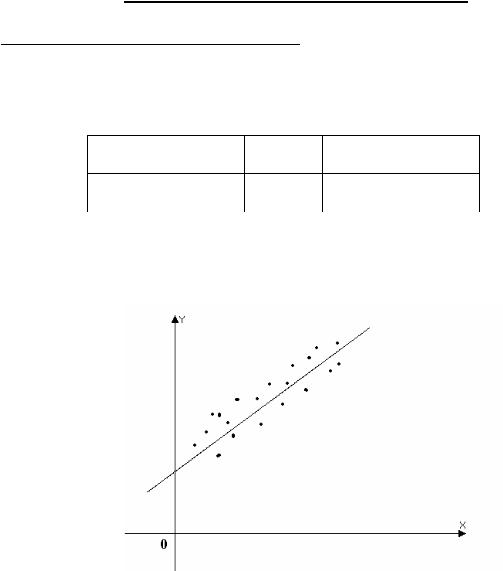
Предположим, что произведены измерения двух величин x и y , связанных некоторой зависимостью y = f (x). Например, x – температура растворителя, y – количество растворяющегося вещества. Результаты измерений сведены в таблицу:
х x1 x2 ... xn
|
y |
y1 |
y2 |
… |
yn |
|
|
|
Измерения неизбежно |
|
содержат |
ошибки. Поэтому точки (xk , yk ), |
k = 1,2,...,n , |
не “лягут” точно на график функции. Например, для линейной |
зависимости |
f (x) = ax + b картинка может иметь вид: |
|
Задача состоит в таком выборе параметров функции f (x), чтобы её график “наилучшим” образом вписывался во множество точек (xk , yk ), k = 1,2,...,n . В качестве меры близости графика к этим точкам наиболее часто используется
- 130 -

сумма квадратов отклонений наблюдённого значения |
yk |
от |
теоретического |
значения f (xk ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = å(yk - f (xk ))2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Те значения |
параметров |
функции |
f (x), которые |
доставляют этой |
сумме |
минимальное значение, считаются “наилучшими”. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае линейной зависимости |
f (x) = ax + b “наилучшие” значения a и b |
минимизируют сумму: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(a,b) = å(yk - (ax + b))2 , |
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е должны обращать в нуль частные производные |
|
S |
¢ |
и |
|
S¢ . |
Вычислим эти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
производные: |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
S¢ |
= |
å |
2(y |
k |
- (ax |
k |
+ b)) ×(-x ) = 2ç |
- |
å |
y |
k |
× x |
k |
+ a × |
å |
x2 |
+ b × |
å |
x |
k |
÷ , |
a |
|
|
|
|
k |
|
|
ç |
|
|
|
|
|
|
k |
|
|
÷ |
|
|
k =1 |
|
|
|
|
|
|
|
|
è |
|
k =1 |
|
|
|
|
|
|
|
k =1 |
|
k =1 |
|
|
ø |
b |
|
n |
|
k |
|
|
|
|
æ |
|
|
n |
|
|
k |
|
|
|
|
n |
|
|
|
|
n |
ö |
|
|
|
|
= |
å |
2(y |
|
|
|
|
ç |
- |
å |
y |
+ a × |
å |
x + b × |
å |
÷ |
|
|
|
|
S¢ |
|
|
- (ax + b)) × (-1) = 2ç |
|
|
|
|
|
|
|
|
1÷. |
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
è k =1 |
|
|
|
|
|
k =1 |
|
|
|
k =1 ø |
|
|
|
|
Итак, для определения стационарной точки функции S(a,b) имеем т. н. систему нормальных уравнений:
ì |
å |
2 |
|
|
|
|
|
|
ïa × |
x |
+ b |
x |
= |
x |
× y |
, |
í |
k |
|
å k |
|
å k |
k |
(2) |
î |
a × |
å k |
+ b × n = |
å k |
. |
|
ï |
|
x |
y |
|
II Одно полезное неравенство
Чтобы исследовать систему (2), а затем и стационарную точку, докажем одно неравенство.
|
Рассмотрим n чисел x1, x2 ,..., xn , исключая случай |
x1 = x2 = ... = xn . |
|
|
|
|
|
|
1 |
|
n |
|
|
|
= |
å xk . Тогда: |
|
Обозначим |
x |
– среднее арифметическое этих чисел: |
x |
|
n |
|
|
|
|
|
|
k |
=1 |
|
|
|
|
|
|
|