2.10. Варіанти індивідуальних завдань

На проміжку [a, b] скласти таблицю значень функції y=f(x) в (n+1)-ой рiвновiддалених вузлових точках. По цій таблиці побудувати інтерполяційні багаточлени Лагранжа й Ньютона. В обох випадках визначити наближені значення функції в точці по формулі. Оцінити погрішністьотриманих значень, зрівняти її з “точною ” погрішністю.

У варіантах 1-12 уважати ,,

у варіантах 13-25, - ,,

де - номер варіанта. Значеннязадається викладачем.

Лекція 3. Методи рішення систем лінійних алгебраїчних рівнянь

У якій розглядаються точні ( Гаусса, Жордана-Гаусса) і наближені ( простої ітерації, Зейделя) методи рішення. З використанням елементів теорії стискаючих відображень розглянуті питання збіжності ітераційних послідовностей і оцінки погрішності наближених рішень.

3.1. Попередні зауваження

У розгорнутому виглядi система n лінійних алгебраїчних рівнянь має вид

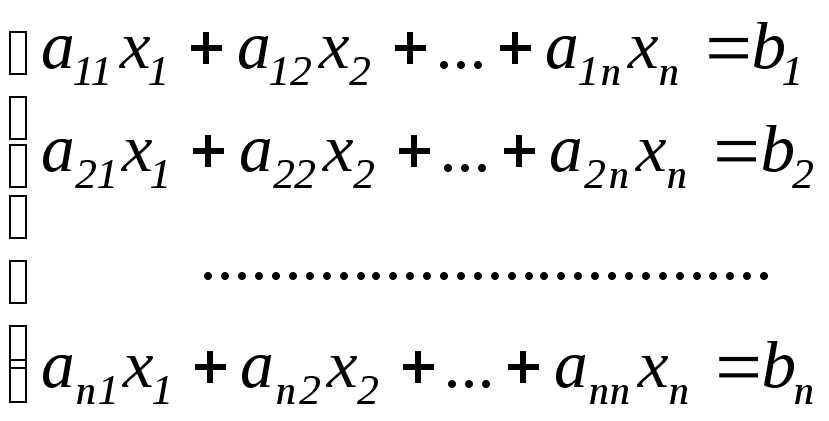(3.1)

де - відомі коефіцієнти,- шукані величини. Якщо позначити через

те (3.1) можна представити й у матричному виді

(3.11)

Рішенням системи (3.1) (або (3.11))називається набір значень , обертаючий кожне з рівнянь системи у вірну рівність.

Необхідні й достатні умови можливості розв'язання системи (3.1) описуються теоремою Кронекера – Капеллi. Припускаючи їх виконаними, зупинимося на розгляді точних і наближених методах її розв’язання.

Точним називається метод, що дозволяє за кінцеве число точно виконуваних операцій одержати точне рішення. У противному випадку метод називається наближеним.

3.2. Точні методи рішення

До числа розповсюджених ставляться метод Гаусса і його модифікація, називана методом Жордана – Гаусса.

Метод Гаусса. Центральною частиною даного методу є процедура приведення вихідної системи рівняння до трикутного, у загальному випадку, трапецієподібному, вигляду. Це здійснюється шляхом еквівалентних перетворень системи в наступній послідовності.

Крок 1. У лівій частині першого рівняння вибирається відмінний від нуля коефіцієнт, що називається провідним або визначальним. Нехай це , у противному випадку доможемося цього, переставивши стовпці й перенумерувавши невідомі. Після цього розділимо перше рівняння на провідний елемент

.

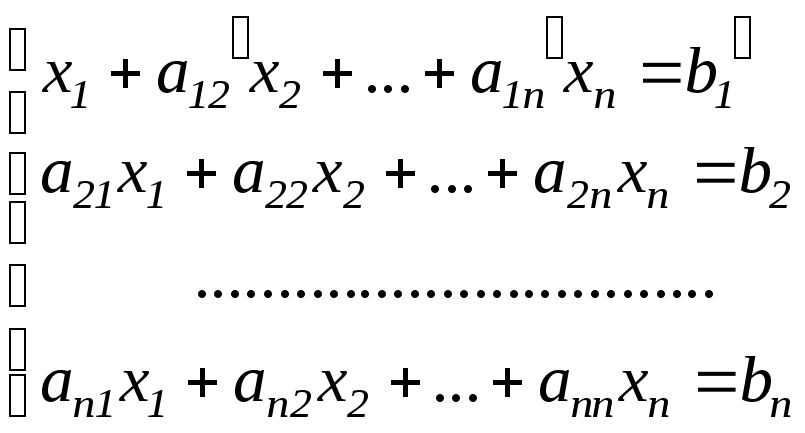Крок 2. Віднімемо почтенно із другого рівняння перше, помножене на , далі, із третього перше, помножене най т.д., нарешті з n-го,- перше, помножене на. У результаті цього одержимо

.

Крок 3. Перше рівняння залишимо незмінним, а в другому,- виберемо провідний елемент, нехай це й розділимо на нього друге рівняння.

Крок 4. Із третього й всіх наступних рівнянь, описаним вище способом, виключимо змінну х₂.

Далі, надходячи в такий же спосіб із третім і іншим рівняннями за кінцеве число кроків приведемо систему до трикутного вигляду

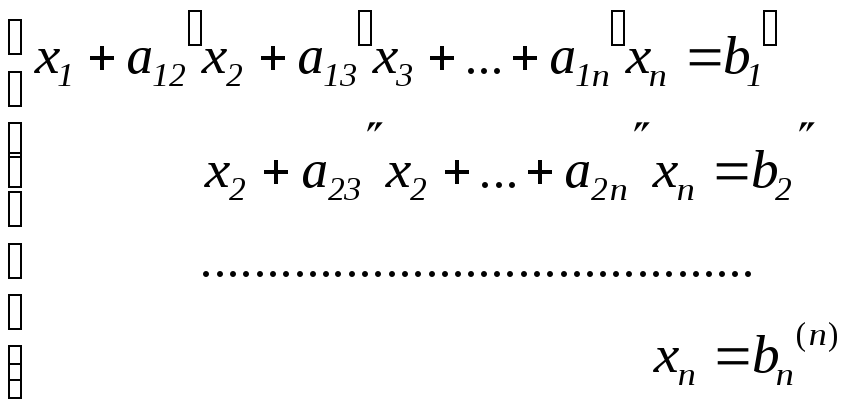(3.2)

якщо рішення єдине, або до трапецеподiбного, якщо рішень нескінченно багато. Якщо ж на якімсь кроці одне з рівнянь прийме вигляд , то це означає несумісність вихідної системи рівнянь.

Описаний процес перетворення системи називається прямим ходом. Припустимо, що в результаті виконання прямого ходу система наведена до виду (3.2). У цьому випадку з останнього рівняння визначається значення . Воно підставляється в попереднє, з якого перебуває . Знайдені значення , підставляються в ( n-2)-е рівняння, з якого перебуває . Далі, діючи аналогічним образом, з ( n-3)-го рівняння визначається значення , з ( n-4)-го, - і, нарешті, з першого – значення . Процес послідовного знаходження із системи (3.2) називається зворотним ходом.

З метою зниження впливу погрішностей округлення, що виникають при виконанні обчислень, як ведучий рекомендується вибирати найбільший по модулі елементи лівої частини рівняння. Дійсно, у цьому випадку коефіцієнти системи (3.2) по модулі не перевищують одиницю й часткові погрішності значенняx_i , обумовлені помилками значеньx_m

не перевищує величини , тобто не зростають.

Метод Жордана -Гаусса. Сполучає виконання прямого й зворотного ходів методу Гаусса. Реалізується в такий спосіб.

Крок 1, 2, 3. Збігаються з першими кроками методу Гаусса.

Крок 4. За допомогою другого рівняння змінна видаляється не тільки з наступних, але й з попереднього, тобто першого рівняння. У результаті цього система приймає вигляд

.

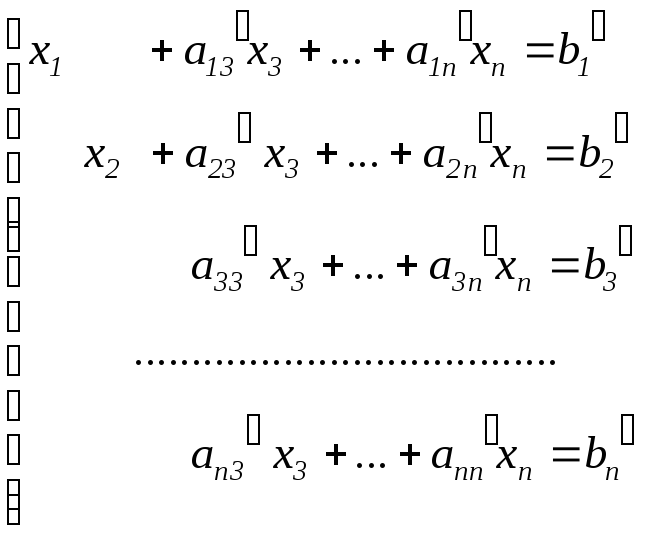Далі, розглядається третє рівняння й з його допомогою описаним способом виключається змінна із всіх інших рівнянь. Надходячи також з кожним наступним рівнянням, і проводячи, бути може, перепозначення невідомих, за кінцеве число кроків система приводиться до виду

.

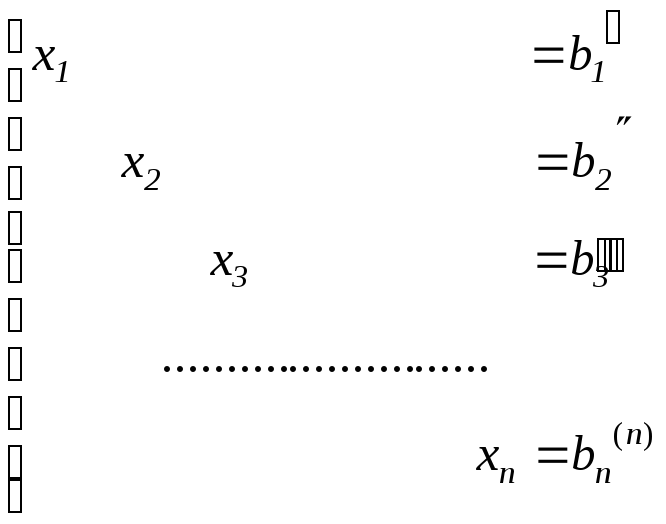Стовпець правих частин і являє собою розв’язок системи рівнянь.

Порівняльний аналіз. З погляду трудомісткості обчислень обидва методи практично еквівалентні. Так, для реалізації методу Гаусса необхідно арифметичних операцій, для виконання методу Жордана-Гаусса,-.

Разом з тим, у літературі відзначається цікава особливість методу Жордана-Гаусса. А саме, якщо внести деякі зміни в порядок його виконання, то можна досягти істотного зниження необхідного об'єму оперативної пам'яті. Так, розглядаючи друге рівняння, використовувати перше для виключення в ньому змінної х₁, після чого використовувати модифіковане друге для виключення змінної х₂ з першого рівняння. Далі, при розгляді третього рівняння використовувати перші два для виключення в них змінних х₁ , х₂ , після чого використовувати третє для виключення з перших двох змінних х₃. І так далі. При такій організації обчислень на кожному кроці в роботі бере участь не вся система, а тільки її частина. Показано, що при рівних об'ємах використовуваної оперативної пам'яті це дозволяє приблизно у два рази, у порівнянні з методом Гаусса, підвищити порядок розв'язуваної системи.

Зауваження. До числа точних ставляться й методи, засновані на розкладанні матриці А лівої частини системи (3.11) у вигляді добутку двох трикутних матриць У и С, тобто А=ВР, де

, .

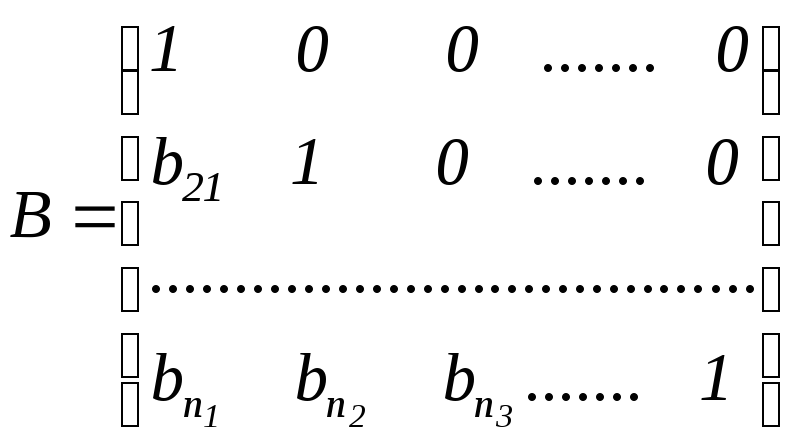У цьому випадку система приймає вигляд

BСХ=b,

і, позначивши Y=CX, замість системи (3.11), маємо дві системи рівнянь із трикутними матрицями

BY=b

CX=Y.

Центральним моментом таких методів є реалізація зазначеного розкладання матриці А. Показане, що для симетричних і неврожденних матриць такі процедури існують.