3. Дискретна форма рядів Фур'є

Розглянемо розкладання (6), (7). Припустимо, що на відрізку функціязадана вm равностоящих вузлових крапках , де,

Використовуючи для обчислення коефіцієнтів формулу лівих прямокутників з (7) маємо

або, з огляду на ,

(8)

Співвідношення (8) називається дискретним перетворенням Фур'є.

Таким чином, з огляду на остаточно маємо

Зі співвідношень (8) випливають наступні властивості.

Властивість 1. Набір коефіцієнтів є комплексно сполученим, тобто

, ,

Дійсно, згідно (8), маємо

Властивість 2. Набір коефіцієнтів ,є періодичним з періодом рівнимm. Т.е. .

Обґрунтовується аналогічним образом.

Наслідок. Для побудови розкладання (8) при чисельному моделюванні з рівновіддаленими вузловими крапками досить обчислення по коефіцієнтів.

Так, при m=3, наприклад, - коефіцієнтів ,. Тоді по властивості 1,аПо властивості 2, -Приm=4 , - коефіцієнтів Тоді, і

8.4. Завдання

1. Розкласти зазначені функції в ряд Фур'є:

- у задачах 1 б), 2 б) представити розкладання в стандартній формі;

- у задачах 1 а), 2 а) представити в комплексній формі.

2. Одержати розкладання зазначених функцій, використовуючи стандартні процедури пакета Matlab.

3. Зрівняти отримані результати для перших n гармонік.

Розкласти зазначені функції в ряд Фур'є в зазначених інтервалах

Варіант 1

1. a), б) , по синусах,

2. а) б) по косинусах,

Варіант 2

1. a), б) , по косинусах,

2. а) , б) по синусах.

Варіант 3

1. a), б) , по косинусах,

2. а) , б) по синусах.

Варіант 4

1. a), б) , по синусах,

2. а) , б) , , по косинусах.

Варіант 5

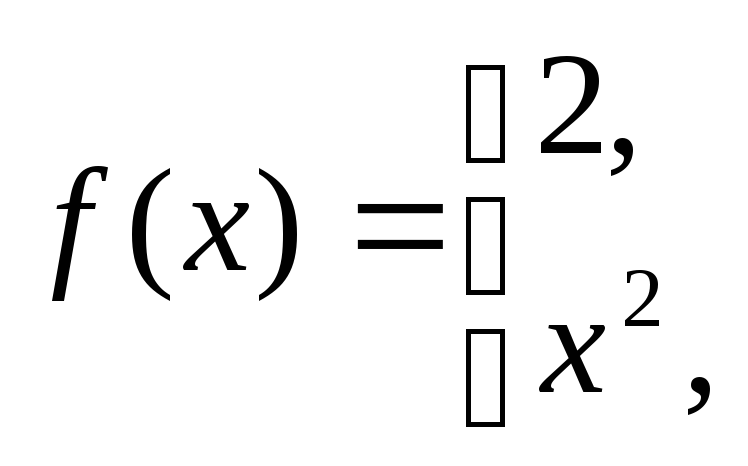
1. a) , б) , по косинусах,

2. а) , , б) , , по синусах.

Варіант 6

1. a) , б) , по косинусах,

2. а) , , б) , по косинусах.

Варіант 7

1. a) , б) , по косинусах,

2. а) , , б) , по синусах.

Варіант 8

1. a) , б) , по синусах,

2. а) , , б) , по косинусах.

Варіант 9

1. a), , б) , по косинусах,

2. а) , , б) по синусах.

Варіант 10

1. a) , б) , по косинусах,

2. a) , б) , по синусах.

Варіант 11

1. a) , б) , по синусах,

2. a) , б) , по косинусах.

Варіант 12

1. a), б) по косинусах,

2. а) , б) по синусах.

Варіант 13

1. a), б) , по синусах,

2. а) б) по косинусах.

Варіант 14

1. a) , б) , по косинусах,

2. а) , , б) , по синусах.

Варіант 15

1. a) , б) , по косинусах,

2. а) , , б) , по синусах.

Варіант 16

1. a) , б) , по синусах,

2. а) , , б) , по косинусах.

Варіант 17

1. a), б) по синусах,

2. а) , б) , , по косинусах.

Варіант 18

1. a) , б) , по косинусах,

2. a) , б) , по синусах

Варіант 19

1. a), б) , по синусах,

2. а) , б) , , по косинусах.

Варіант 20

1. a), б) по косинусах,

2. а) , б) , по синусах.

Варіант 21

1. a) , б) , по синусах,

2. а) , , б) , по косинусах.

Варіант 22

1. a) , б) , по косинусах,

2. а) , , б) , по синусах.

Варіант 23

1. a) , б) , по синусах,

2. а) , , б) , по косинусах.

Варіант 24

1. a) , б) , по косинусах,

2. а) , , б) по синусах.

Варіант 25

1. a), б) , по синусах,

2. а) , б) , , по косинусах.

Додаткова література

1. В.И. Крилов, В.В. Бобків, П.И. Монастырный. Обчислювальні методи. В 2-х томах. - М. Наука, 1976.

2. Р.В. Хемминг. Чисельні методи для науковців і інженерів. - М.: Мир, 1968.

3. Д.Н. Фаддеев, В.Н. Фаддеева. Обчислювальні методи лінійної алгебри. - Спб.: Видавництво «Лань», 2002.

4. С.В. Поршнєв. Обчислювальна математика. Курс лекцій. - Спб.: БХВ- Петербург, 2004.